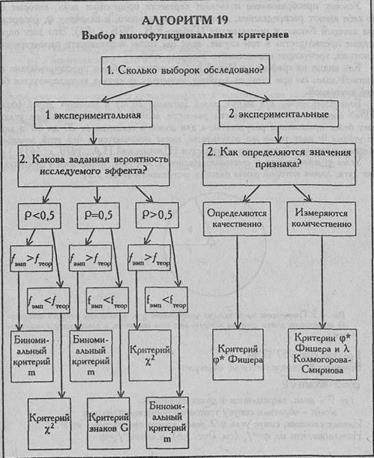
Алгоритм выбора многофункциональных критериев

5.7. Математическое сопровождение к описанию критерия φ* Фишера

Угловое преобразование позволяет перевести процентные доли, которые сами по себе имеют распределение, далекое от нормального, в величину φ, распределе­ние которой близко к нормальному (Гублер Е.В., 1978, с. 84). Это дает опреде­ленные преимущества в том случае, если мы хотим использовать параметрические критерии, требующие нормальности распределений.

Как видно из графика на Рис. 5.1, φ нарастает в общем пропорционально про­центной доле, но при этом на крайних значениях φ кривая характеризуется боль­шей крутизной.

Благодаря этому для малых долей (меньше 20%) и больших долей (больше 80%) определение достоверности разности долей по соответствующим углам φ дает более правильные результаты, а для долей в пределах от 20 до 80% замена их углами φ дает такие же результаты, какие получаются и без этой замены, но техника вычислений при этом упрощается (Плохинский Н.А., 1970, с. 143).

Углы φ измеряются в радианах. Радиан - это угол, являющийся центральным для дуги, длина которой равна радиусу окружности (Рис. 5.5).

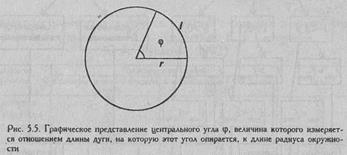
1 радиан равен 57°17'44".

Величина φ определяется по формуле:

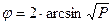
где Р - доля, выраженная в долях единицы;

arcsin - обратная синусу тригонометрическая функция.

Иными словами, синус угла φ/2 равен корню квадратному из Р. Напомним, что sinφ=^а/_с (см. Рис. 5.6), a arcsin ^а/_с= φ

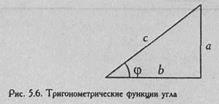
Величину φ можно вычислить в радианах или определить по специальной таб­лице (Табл. XII Приложения 1).

Н.А. Плохинский использует иную формулу определения ф:

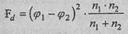
где φ₁ - значение угла для первой доли;

φ₂- значение угла для второй доли;

n₁ - количество наблюдений в первой выборке;

n₂ - количество наблюдений во второй выборке.

Эмпирические значения F_d сопоставляются с критическими значениями крите­рия F Фишера, которые определяются по таблице для степеней свободы v₁ и v₂, определяемых как:

По нашему опыту, этот вариант критерия с использованием углового преобра­зования дает менее точные результаты, чем вариант Е.В. Гублера (1978).

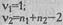
ГЛАВА 6 МЕТОД РАНГОВОЙ КОРРЕЛЯЦИИ

Дата добавления: 2015-06-04