Решение задачи 6

Решения задач Главы 4

Вопрос 1: Можно ли утверждать, что разные картины методики Хекхаузена обладают разной побудительной силой в отношении моти­вов: а) "надежда на успех"; б) "боязнь неудачи"?

Для того, чтобы ответить на этот вопрос, необходимо сопоставить распределение реакций "надежда на успех" и реакций "боязнь неудачи" с равномерным распределением. Тем самым мы проверим, равномерно ли распределяются реакции "надежды на успех" по шести картинам и равно­мерно ли распределяются реакции "боязни неудачи" по шести картинам.

Количество наблюдений достаточно велико, чтобы мы могли ис­пользовать любой из классических критериев - χ ² или λ. Однако, как мы помним, картины в данном исследовании предъявлялись разным испытуемым в разных последовательностях, следовательно, мы не мо­жем говорить об однонаправленном изменении признака в какую-либо одну сторону: все разряды (картины) следуют друг за другом в слу­чайном порядке. Это является веским основанием для применения кри­терия χ ² и отказа от критерия λ.

Рассмотрим оба аспекта поставленного вопроса последовательно.

А) Равномерно ли распределяются реакции "надежды на успех" по шести картинам методики Хекхаузена?

H₀: Распределение реакций "надежды на успех" не отличается от рав­номерного распределения.

H₁: Распределение реакций "надежды на успех" отличается от равно­мерного распределения.

Рассчитаем теоретические частоты для равномерного распределе­ния по формуле:

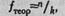
где n - количество наблюдений,

k - количество разрядов.

В данном случае количество наблюдений - это количество реак­ций "надежды на успех" у 113 испытуемых. Таких реакций зарегистри­ровано 580, следовательно, n =580. Количество разрядов - это количе­ство стимульных картин, следовательно, k=6. Определяем f _теор:

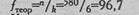
Количество степеней свободы V определяем по формуле:

v = k -l=6-l=5

Итак, поправка на непрерывность не нужна, мы можем произво­дить все расчеты по общему алгоритму. Они представлены в Табл.9.11.

Таблица 9.11

Расчет критерия χ ² при сопоставлении распределения реакций "надежды на успех" по 6 картинам с равномерным распределением

Разряды-картины методики	Эмпирические частоты реакций "надежды на успех" fэ	Теоретические частоты реакции "надежды на успех" fт	fэ- fт	(fэ- fт)^2	(fэ- fт)^2/ fт
	"Мастер изме­ряет деталь" "Преподаватель и ученик" "В цехе у машины" "У двери ди­ректора" "Человек в бюро" "Улыбающийся юноша"		96,67   96,67   96,67   96,67   96,67   96,67	9,33   5,33 11,33   -46,67   2,33   18,33	87,05   28,41   128,37   2178,09   5,43   335,99	0,90   0,29   1,33   22,53   0,06   3,48
Суммы					28,59

По Табл. IX Приложения 1 определяем критические значения χ ² для v =5:

Построим "ось значимости".

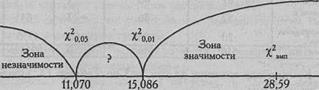
χ²_эмп = 28,59

χ²_эмп > χ²_кр

Ответ: H₀ отклоняется. Принимается H₁. Распределение реак­ций "надежды на успех" по шести картинам методики Хекхаузена от­личается от равномерного распределения (р <0,01).

Б) Равномерно ли распределяются реакции "боязни неудачи" по шести картинам методики Хекхаузена?

H₀: Распределение реакций "боязни неудачи" не отличается от равно­мерного распределения.

H₁: Распределение реакций "боязни неудачи" отличается от равномер­ного распределения.

В данном случае количество наблюдений - это число реакций "боязни неудачи", следовательно, n =516; количество разрядов - это число стимульных картин, как и в предыдущем случае, следовательно, k=6. Определяем f _теор

f _теор =⁵¹⁶/₆=86

Количество степеней свободы v = k —1=6—1=5. Поправка на не­прерывность здесь тоже, естественно, не нужна.

Все дальнейшие расчеты проделаем по алгоритму в таблице.

Таблица 9.12

Расчет критерия при сопоставлении распределения реакций "боязни неудачи" по 6 картинам с равномерным распределением

Разряды-картины методики	Эмпирические частоты реакций "боязни неудачи" fэ	Теоретические частоты реакции "боязни неудачи" fт	fэ- fт	(fэ- fт)^2	(fэ- fт)^2/ fт
	"Мастер изме­ряет деталь" "Преподаватель и ученик" "В цехе у машины" "У двери ди­ректора" "Человек в бюро" "Улыбающийся юноша"			-52     -29   -66		31,44   102.74   31,44   0.01   9.78   50,65
Суммы					226,06

Критические значения χ²при v =5 по Таблице IX Приложения 1 нам уже известны:

χ²_эмп > χ²_кр

Ответ: H₀ отклоняется. Принимается H₁. Распределение прояв­лений "боязни неудачи" по шести стимульным картинам отличается от равномерного распределения (р <0,01).

Итак, реакции "надежды на успех" и реакции "боязни неудачи" неравномерно проявляются в ответ на 6 стимульных картин. Однако это еще не означает, что эти картины являются неуравновешенными по направленности воздействия. Может оказаться так, по крайней мере теоретически, что одни и те же картины вызывают большинство реакций обоих типов, а другие картины почти не вызывают реакций или вызывают их достоверно меньше. В этом случае оба эмпирических распределения отличались бы от равномерного, но не различались бы между собой.

Проверим, различаются ли картины теперь уже не по количеству вы­зываемых реакций, а по их качеству, то есть вызывают ли одни картины скорее реакции "надежды на успех", а другие - реакции "боязни неудачи"

Вопрос 2: Можно ли считать стимульный набор методики Хекхаузена неуравновешенным по направленности воздействия?

Решим эту задачу двумя способами: а) путем сравнения распре­деления реакций "надежда на успех" с распределением реакций "боязнь неудачи" по 6-и картинам; б) путем сопоставления распределения реак­ций на каждую картину с равномерным распределением.

Выясним, совпадают ли распределения реакций по двум карти­нам. Для этого сформулируем гипотезы.

H₀: Распределения реакций "надежда на успех" и реакций "боязнь не­удачи" не различаются между собой.

H₁: Распределения реакций "надежда на успех" и "боязнь неудачи" различаются между собой.

Для того, чтобы облегчить себе задачу подсчета теоретических частот, воспроизведем таблицу эмпирических частот и дополним ее.

Таблица 9.13

Эмпирические и теоретические частоты распределения реакций "надежда на успех" и "боязни неудачи"

Разряды - картины	Эмпирические частоты	Суммы	Теоретические частоты	Суммы
Реакций "надежда на успех"	Реакций "боязнь неуда­чи"		Реакций "надежда на успех"	Реакций "боязнь неуда­чи"
	"Мастер измеря­ет деталь" "Преподаватель и ученик" "В цехе у маши-   "У двери дирек­тора"   "Человек в бюро"   "Улыбающийся юноша"		А   В   д   ж   и   л		Б   Г   Е     К   M		129,1   149,2   75,1   72,5   82,6   71,4	А   В   Д   Ж   И   Л	114,9   132,8   66,9   64,5   73,4   63,6	Б   Г   Е     К   М
Суммы

Расчет теоретических частот осуществляется по известной нам формуле:

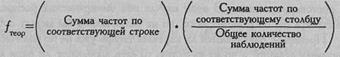
Произведем расчеты.

f_{А теор}=244·580/1096=129,1

f_{Б теор}=244·516/1096=114,9

f_{В теор}=282·580/1096=149,2

f_{Г теор}=282·516/1096=132,8

f_{Д теор}=142·580/1096=75,1

f_{Е теор}=142·516/1096=66,9

f_{Ж теор}=137·580/1096=72,5

f_{З теор}=137·516/1096=64,5

f_{И теор}=156·580/1096=82,6

f_{К теор}=156·516/1096=73,4

f_{Л теор}=135·580/1096=71,4

f_{М теор}=135·516/1096=63,6

По Табл. 9.13 мы видим, что сумма всех теоретических частот равна общему количеству наблюдений, а попарные суммы теоретических частот по строкам равны суммам наблюдений по строкам.

Расчеты критерия χ²будем производить по известному алгоритму. Поправка на непрерывность не вносится, так как v >1:

v =(r -l)(c -l)=(6-l)(2-l)=5

Результаты всех операций по Алгоритму 13 представлены в Табл. 9.14.

Таблица 9.14

Расчет критерия χ²при сопоставлении эмпирических распределений реакций "надежды на успех" (НУ) и "боязни неудачи" (БН)

Ячейки таблицы частот	Эмпирическая частота fэ	Теоретическая частота fт	fэ- fт	(fэ- fт)^2	(fэ- fт)^2/ fт
	А		129,1	-23,1	533,61	4,13
	Б		114,9	23,1	533,61	4,64
	В		149,2	-47,2	2227,84	14,93
	Г		132,8	47,2	2227,84	16,78
	Д		75,1	32,9	1082,41	14,41
	Е		66,9	-32,9	1082,41	16,18
	Ж		72,5	-22,5	506,25	6,98
			64,5	22,5	506,25	7,85
	И		82,6	16,4	268,96	3,26
	К		73,4	-16,4	268,96	3,66
	Л		71,4	43,6	1900,96	26,62
	М		63,6	-43,6	1900,96	29,89
Суммы,					149,33

Критические значения χ²при v =5 нам уже известны:

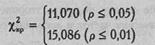
Построим "ось значимости".

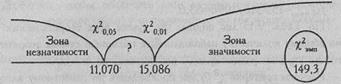
χ²_эмп > χ²_кр

Ответ: H₀ отвергается. Принимается H₁. Распределения реакций "надежды на успех" и "боязни неудачи" различаются между собой.

Теперь выясним, совпадают ли распределения реакций по каждой картине. Сформулируем гипотезы.

H₀: Реакции двух видов в ответ на картину №1 (№2, №3... №6) распределяются равномерно.

H₁: Реакции двух видов в ответ на картину №1 (№2, №3... №6) распределяются неравномерно.

Реакции "надежды на успех" будем обозначать как НУ, реакции "боязни неудачи" - как БН.

Подсчитаем теоретические частоты для каждой из шести картин, по формуле:

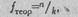
где n общее количество реакций обоих направлений на данную картину; k - количество разрядов, в данном случае количество видов реакции (k =2).

f_{1 теор} =244/2=121;

f_{2 теор} =282/2=141;

f_{3 теор} =142/2=71;

f_{4 теор} =137/2=68,5

f_{5 теор} =156/2=78

f_{6 теор} =135/2=67,5

В данном случае число степеней свободы v =l:

v = k —1=2—1=1.

Следовательно, мы должны сделать во всех шести случаях по­правку на непрерывность. Проведем расчеты отдельно для каждой кар­тины (см. Табл. 9.15).

Таблица 9.15

Расчет критерия χ²при сопоставлении распределений реакций на каж­дую из шести картин с равномерным распределением

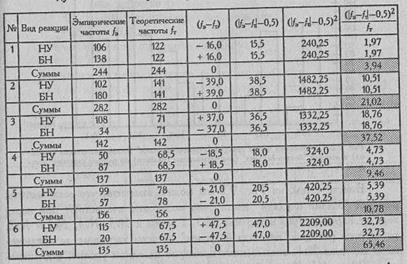
Определим по Табл. IX Приложения 1 критические значения для v =l:

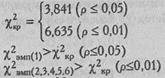
Ответ: H₀ отклоняется для всех картин. H₁принимается для картин 2, 3, 4, 5 и 6: реакции двух видов в ответ на эти картины рас­пределяются неравномерно.

Если представить данные графически (Рис. 9.2), то легко можно видеть, что картины №6, №3 и №5 вызывают достоверно больше реакций "надежды на успех", а картины №2, №1 и №4 - достоверно больше реакций "боязни неудачи".

Стимульный набор методики Х. Хекхаузена оказался неуравнове­шенным по направленности стимулирующего воздействия.

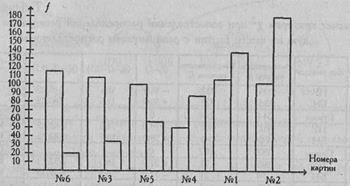
Рис. 9.2. Соотношения частот реакций "надежда на успех" (незаштрнхованные столбн-ки) н реакций "боязнь неудачи" (заштрихованные столбики) по разным картинам мето­дики Х.Хекхаузена

Вместе с тем, из Рис. 9.2 мы можем заметить, что если частоты реакций "боязни неудачи" достаточно монотонно возрастают при пере­ходе от картины №6 к картине №3, а затем к №5, №4, №1 и №2, то частоты реакций "надежда на успех" по всем картинам, за исключе­нием картины №4, оказываются примерно на одном уровне, в диапазо­не от 99 до 115. Каждый исследователь сам для себя решает вопрос о том, что для него важнее - абсолютные показатели стимулирующего воздействия или их соотношения. Метод у} поможет ему решить зада­чи и первого, и второго типа.

Дата добавления: 2015-06-04