Решение задачи 8

Вопрос 1: Различаются ли распределения предпочтений, выявлен­ные по каждому из четырех типов мужественности, между собой?

Для выявления различий между четырьмя распределениями лучше всего применить критерий χ². Критерий λне применим по трем причи­нам: 1) n <50; 2) разряды представляют собой номинативную шкалу, так как при переходе от типа к типу изменяется "качество", а не "количество" мужественности; 3) критерий λ позволяет сопоставлять только 2 распределения одновременно, а в нашу задачу входит одно­временное сопоставление четырех распределений.

Сформулируем гипотезы.

H₀: Распределения предпочтений, выявленные по четырем типам муже­ственности, не различаются между собой.

H₁: Распределения предпочтений, выявленные по четырем типам муже­ственности, различаются между собой.

Рассчитаем теоретические частоты для каждой ячейки таблицы эмпирических частот (Табл. 9.18) по формуле:

f_{А теор} =31-31/124=7.75

f_{Б теор} =31-31/124=7,75 и т. д.

Поскольку суммы по всем строкам и столбцам таблицы равны, теоретические частоты для всех 16-ти ячеек таблицы будут одинаковы­ми. Равенство же по строкам и столбцам объясняется тем, что каждая испытуемая совершала принужденный выбор, так что каждый из типов мужественности был выбран 31 раз (даже если он был "выбран на последнее место).

Эта задача напоминает шутливый литературный пример, в кото­ром одна невеста совершала выбор из четырех женихов. В данном же случае у нас 31 испытуемая, и каждая совершает выбор из четырех ти­пов мужественности, распределяя их по четырем позициям.

Определим количество степеней свободы V для четырех типов мужественности (k) и четырех позиций выбора (с):

v =(k -l)-(c-l)=(4-l) (4-l)=3·3=9

Все дальнейшие расчеты произведем в таблице по Алгоритму 13 без поправки на непрерывность, так как при v >1 она не требуется.

Таблица 9.18

Расчет критерия χ²при сопоставлении распределений четырех типов мужественности по четырем позициям (n =31)

Разряды- типы мужественности	Позиции выбора	Эмпирическая частота fэ	Теоретическая частота fт	fэ- fт	(fэ- fт)^2	(fэ- fт)^2/ fт
1. Мифологически тип			7,75	-5,75	33,063	4,266
		7,75	-1,75	3,063	0,395
		7,75	-3,75	14,063	1,815
		7,75	+11,25	126,563	16,331
2. Национальный ТИП			7,75	+11,25	126,563	16,331
		7,75	-3,75	14,063	1,815
		7,75	-0,75	0,563	0,073
		7,75	-6,75	45,563	5,879
3, Современный ТИП			7,75	-0,75	0,563	0,073
		7,75	+2,25	5,063	0,653
		7,75	+4.25	18,063	2,331
		7,75	-5,75	33,063	4,266
4, Религиозный ТИП			7,75	-4,75	22,563	2,911
		7,75	+3,25	10,563	1,362
		7,75	+0,25	0,063	0,008
		7,75	+1,25	1,563	0,202
Суммы			124,0			58,711

По Табл. IX Приложения 1 определяем критические значения χ² при V=9:

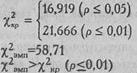
Ответ: H₀ отвергается. Принимается H₁. Распределения пред­почтений по четырем типам мужественности различаются между собой.

Вопрос 2. Можно ли утверждать, что предпочтение отдается ка­кому-то одному или двум типам мужественности? Наблюдается ли ка­кая-либо групповая тенденция предпочтений?

В данном случае удобнее всего применить критерий χ² _r Фридма­на (см. Главу 3). Как мы помним, он позволяет выявить изменения в величине признака при переходе от одного условия к другому. По-видимому, еще более целесообразным было бы применить тест тенден­ций L Пейджа, но при n >12 это можно сделать только с помощью специальных ухищрений (см. Задачу 4 и ее решение).

Критерий χ² _r позволяет определить, достоверным ли образом различаются суммы рангов, полученные по каждому из рассматривае­мых условий, в данном случае - по каждому типу мужественности.

При этом ранги начисляются отдельно по каждому испытуемому, а суммируются - по каждому условию. В нашем случае нет необходи­мости что-то ранжировать, так как каждая испытуемая своими выбора­ми фактически уже проранжировала четыре исследуемых типа мужест­венности. Суммы рангов по каждому типу мужественности можно под­считать, умножая значение ранга на количество рангов с данным значе­нием. Например, из Табл. 9.18 следует, что Мифологический тип 2 раза оказался в первой позиции. Значит, сумма рангов по 1-й позиции будет равна: 1·2=2. На второй позиции он оказался 6 раз, следователь­но, сумма рангов по 2-й позиции равна: 2·6=12 и т. д. Произведем расчеты в таблице. Для 3-й позиции Мифологического типа сумма рангов составит 3·4=12, а для 4-й: 4·19=76. Теперь определяем общую сумму рангов Мифологического типа: 2+12+12+76=102.

Таблица 9.19

Расчет ранговых сумм по четырем типам мужественности (n =31) для подсчета критерия χ² _r.

Значение ранга	Типы мужественности
Мифологический	Национальный	Современный	Религиозный
faj	faj · rj	faj	faj · rj	faj	faj · rj	faj	faj · rj

Суммы рангов

Сформулируем гипотезы.

H₀: Различия в позициях, которые занимают каждый из четырех типов мужественности, случайны,

H₁: Различия в позициях, которые занимают каждый из четырех типов мужественности, неслучайны. Определим эмпирическую величину χ² _r по формуле:

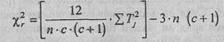
где с - количество условий, в данном случае типов мужественности; п - количество испытуемых; Т _j - суммы рангов по каждому из условий.

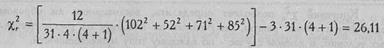
Критические значения определяем по Табл. IX Приложения 1, поскольку при больших п χ² _r имеет распределение, сходное с распреде­лением χ², а существующие таблицы χ² _r предназначены только для n ≤9.

Количество степеней свободы определим так же, как мы это де­лали при расчете критерия χ²:

v =(k -l)(c-l)=(4-l) (4~l)=3·3=9

При v =9 критические значения χ² _r составляют:

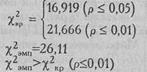
Ответ: Н_о отвергается. Принимается H₁. Различия в позициях, которые занимает каждый из четырех типов мужественности, неслучай­ны (р <0,01). При этом на первом месте оказывается Национальный тип, на втором - Современный, на третьем - Религиозный и на четвер­том - Мифологический тип. На Рис. 9.3. групповая система предпочте­ний представлена графически.

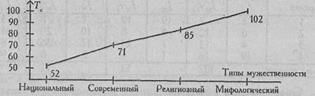
Рис. 9.3. Графики изменения ранговых сумм в последовательности: Национальный тип, Современный тип. Религиозный тип. Мифологический тип; меньшая сумма рангов ука­зывает на большую предпочтительность типа, большая сумма - на меньшую предпочти­тельность

Итак, различия в ранговых местах каждого из рассматриваемых типов мужественности неслучайны. Наблюдается определенная группо­вая тенденция предпочтений. Судя по достаточно монотонному повыше­нию кривой на Рис. 9.3, мы вряд ли можем говорить о резком преоб­ладании какого-либо одного из двух типов мужественности. Для стати­стически достоверного ответа на этот вопрос необходимо сопоставить попарно все типы мужественности по схеме, использованной при реше­нии Задачи 7.

Дата добавления: 2015-06-04