Решение задачи 7

Вопрос 1: Можно ли утверждать, что распределение запретов не является равномерным?

Поскольку количество разрядов (запретов) k>3, иперечень из пяти запретов представляет собой номинативную шкалу, мы можем ис­пользовать только критерий χ².

Если бы участники тренинга называли разные запреты с одина­ковой частотой, то каждый из пяти запретов встречался бы равноверо­ятно с остальными.

Сформулируем гипотезы.

H₀: Распределение частот встречаемости пяти запретов не отличаетсяот равномерного распределения.

H₁: Распределение частот встречаемости пяти запретов отличается от равномерного распределения.

Определим f _теор по формуле:

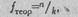
где n - общее количество наблюдений, в данном случае назван­ных запретов (n =281); k - количество категорий запретов (k =5).

f _теор =281/5=56,2

Определим число степеней свободы v:

v = k -l=5-l=4.

Поправки на непрерывность делать не требуется. Все расчеты представим в таблице, строго следуя Алгоритму 13.

Таблица 9.16

Расчет критерия χ²при сопоставлении эмпирического распределения частот встречаемости 5-и психологических запретов с равномерным распределением

Разряды - вид запрета	Эмпирическая частота fэ	Теоретическая частота fт	fэ- fт	(fэ- fт)^2	(fэ- fт)^2/ fт
1, Не давай психологических поглаживаний 2. Не принимай... 3. Не проси... 4. Не отказывайся... 5. Не давай себе...		56,2     56,2 56,2 56,2 56,2	-12,2     -11,2 +41,8 +1,8 -20,2	148,8     125,4 1747,2 3,2 408,0	2,65     2,23 31,09 0,06 7,26
Суммы					43,29

Определим критические значения χ²по Таблице IX Приложения 1 для v =4:

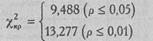
Построим "ось значимости"

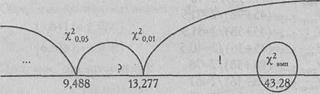
Ответ: χ²_эмп > χ²_кр (р ≤0,01)

H₀ отклоняется. Принимается H₁. Распределение частот встре­чаемости пяти психологических запретов отличается от равномерного распределения (р <0,01).

Вопрос 2: Можно ли утверждать, что запрет "Не проси" встре­чается достоверно чаще остальных?

Для того, чтобы ответить на этот вопрос, мы можем попробовать сопоставить запрет "Не проси" последовательно со всеми остальными запретами, объединяя их попарно.

H₀: Распределение выборов между запретами "Не проси" и "Не да­вай" не отличается от равномерного распределения.

H₁: Распределение выборов между запретами "Не проси" и "Не давай" отличается от равномерного распределения.

Аналогичные гипотезы могут быть сформулированы для всех остальных пар запретов.

При сопоставлении двух запретов число разрядов k=2, следовательно, количество степеней свободы v = k —1=1. Это означает, что нам необходимо делать поправку на непрерывность.

Рассчитаем теоретические частоты для каждой из сопоставляемых пар запретов.

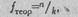
где п - сумма частот, приходящихся на данную пару запретов; k - количество сопоставляемых категорий запретов (k= 2 ).

Определим теоретические частоты для всех возможных пар запретов.

f _{теор 1-2}=(44+45)/2=44,5

f _{теор 1-3}=(44+98)/2=71

f _{теор 1-4}=(44+58)/2=51

f _{теор 1-5}=(44+36)/2=40

f _{теор 2-3}=(45+98)/2=71,5

f _{теор 2-4}=(45+58)/2=51,5

f _{теор 2-5}=(45+36)/2=40,5

f _{теор 3-4}=(98+58)/2=78

f _{теор 3-5}=(98+36)/2=67

f _{теор 4-5}=(58+36)/2=47

Теперь подсчитаем значения критерия χ² (Табл. 9.17).

Таблица 9.17. Расчет значений критерия при попарном сопоставлении частот запретов

Сопоставляемые виды запретов	Эмпирические частоты fэ	Теоретические частоты fт	(fэ – fт)	(|fэ – fт| -O,5)	(|fэ – fт| -O,5)^2	(|fэ – fт| -O,5)^2 ^__________ fт
	«Не давай» «Не принимай Суммы		44,5 44,5   99,0	-0,5 + 0,5
	«Не давай» «Не проси» Суммы		71,0 71,0 142,0	-27,0 + 27,0	26,5 26,5	702,25 702,25	9,89 9,89 19,78
	«Не давай» «Не отказывайся» Суммы		51,0 51,0   102,0	-7,0 + 7,0	6,5 6,5	42,25 42,25	0,83 0,83   1.66
	«Не давай» «Не давай себе» Суммы		40,0 40,0   80,0	+ 4,0 -4,0	3,5 3,5	12,25 12,25	0,31 0,31   0,62
	«Не принимай» «Не проси» Суммы		71,5   71,5 143,0	-26,5   +26,5	26,0   26,0	676,00   676,00	9,45   9,45 18,90
	«Не принимай» «Не отказывайся» Суммы		51,5   51,5   103,0	-6,5   + 6,5	6,0   6,0	36,00   36,00	0,70   0,70   1,40
2 5	«Не принимай» «Не давай себе» Суммы		40,5   40,5   81,0	+ 4,5   -4,5	4,0   4,0	16,00   16,00	0,40   0,40   0,80
3 4	«Не проси» «Не отказывайся» Суммы		78,0 78,0   156,0	+ 20,0 -20,0	19,5 19,5	380,25 380,25	4,88 4,88   9,76
3 5	«Не проси» «Не давай себе* Суммы		67,0 67,0   134,0	+ 31,0 -31,0	30,5 30,5	930,25 930,25	13,88 13,88   27,76
4 5	«Не отказывайся» «Не давай себе» Суммы		47,0   47,0   94,0	+ 11,0   -11,0	10,5   10,5	110,25   110,25	2,35   2,35   4,70

Определим критические значения χ²для v =l:

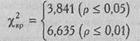
Построим "ось значимости".

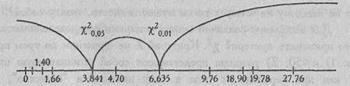
Мы видим, что в некоторых случаях χ²_эмп > χ²_кр, а в некоторых - χ²_эмп < χ²_кр.

Мы можем суммировать полученные данные, построив матрицу, в которой какими-либо знаками будет отмечено, являются ли различия между данной парой запретов достоверными или недостоверными. На­пример, это могут быть указания на уровень значимости различий.

Запреты	1 запрет 2 запрет 3 запрет 4 запрет 5 запрет
1 запрет	—	—	p <0,01	—	—
2 запрет		—	р <0,01	—	—
3 запрет			—	р <0,01	р <0,01
4 запрет				—	p <0,05
5 запрет					—

Итак, выявлены достоверные различия в частоте встречаемости запрета 3 по сравнению со всеми остальными запретами (р<0,01 во всех четырех случаях) и запрета 4 по сравнению с запретом 5 (р<0,05).

Ответ: Hq отклоняется для пар запретов 1—3, 2—3, 3—4, 3—5 (р <0,01) и пары 4—5 (р <0,05). Запрет "Не проси психологических поглаживаний от других людей" встречается достоверно чаще, чем все остальные четыре запрета (р <0,01). Запрет "Не давай психологических поглаживаний самому себе" встречается реже, чем запрет "Не отказы­вайся от психологических поглаживаний, даже если они тебе не нравят­ся" (р <0,05). Обсуждение этих данных представлено в другой работе (Сидоренко Е. В., 1995, с. 65-67).

Дата добавления: 2015-06-04