Аналогичные соотношения- для второй продукции и т.д

Заметим, что именно от конечного продукта зависит успешность компании на рынке и ее показатели роста.

х_1,1 + х_1,2 +…..х _1,n + y₁ = x₁

х_2,1 + х_2,2 +…..х _2,n + y₂ = x₂

……………………

х_n,1 + х_n,2 +…..х _n,n + y_n = x_n

C учетом формулы (1) полученные уравнения перепишем так:

x₁ = α₁₁ x₁ + α₁₂ x₂ +… α_1n x_n + y₁

x₂ = α₂₁ x₁ + α₂₂ x₂ +… α_2n x_n + y₂

…………………………………..

x_n = α_n1 x₁ + α_n2 x₂ +… α_nn x_n + y_n

Хорошо знакомая система линейных алгебраических уравнений!

Осталось записатьэту систему в матричной форме: (что вполне доступно студенту 2 курса)

Х = АХ + У, где

А- матрица коэффициентов α _{i j}, (технологическая матрица)

Перепишем матричное уравнение так:

ЕХ = АХ + У, где Е- единичная матрица, или так:

(Е-А)Х = У или так

Х = (E – A)^-1 У (2)

Уравнение (2)- уравнение Леонтьева. Оно и дает ответ на основной вопрос межотраслевого баланса - принять решение, каким должен быть валовый продукт каждой отрасли (Х =?), чтобы хозяйство в целом произвело заданный конечный продукт У.

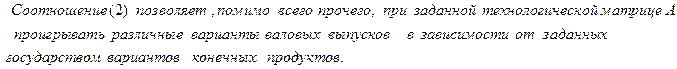
Замечание:

Если для любого столбца У > 0 существует неотрицательное решение системы (2) (а это нам и нужно), то матрица А называется продуктивной. Оказывается, матрица продуктивна, если наибольшая из сумм элементов в столбцах не превосходит единицы, причем для хотя бы одного столбца сумма меньше единицы.

Пример: данные баланса трех отраслей промышленности за год приведены в таблице

Потребители	металлургия	машиностроение	нефтянка	Х	У
Производители
металлургия
машиностроение
нефтянка

В наших обозначениях, х₁ =102, у₁ = 40, х₁₁ =6, х₁₂= 36, х₁₃= 20 и т.д.

Из таблицы видно, что металлургия за год произвела всего 102 ед. продукции, из которых 6 ед. пошло собственно на нужды металлургии, 36 ед. отдано машиностроению и 20 ед. нефтянке. Кроме того, 40 ед. это конечный продукт, предназначенный для реализации во внешней сфере.

Проверим баланс: 6+36+20+40=102- верно!

Аналогично, рассматриваются и другие отрасли в таблице.

Допустим, что конечный продукт У не устраивает плановые органы государства или совета директоров. Ставится задача, найти новый валовый (совокупный) продукт (Х=?), при котором конечный продукт(т.е. реализация) достигнет нового уровня Y= .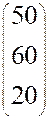

Составим технологическую матрицу:

А=

(продуктивность матрицы очевидна!)

Е – А =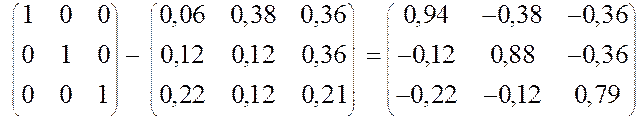

(Е – А)^-1 =

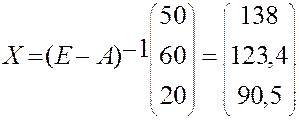
ВЫВОД:

Чтобы обеспечить требуемый конечный продукт, металлургия должна произвести совокупный продукт в объеме 138, машиностроение- 123,4 нефтянка- 90,5.

Дата добавления: 2015-06-04