По условию,

Построим математическую модель.

Менеджеру фирмы требуется принять решение-составить оптимальный план выпуска изделий из условия максимальной прибыли.

В первой строке эти же отрасли представлены, как потребляющие

3. х _{i j} – указывает объем продукции i-й отрасли, потребляемой j – й отраслью.

4. Столбец Х – совокупный (валовый) продукт каждой отрасли за год

5. Столбец У – объем продукции, предназначенной для реализации, т.е конечный продукт каждой отрасли за год,

§ 2. Модели линейного программирования (linear programming ).

Задача л инейного программирования- это такая задача, в которой определеное выражение (критерий, целевая функция) должно быть оптимизировано при наличии ряда ограничений. При этом, как целевая функция, так и ограничения представляют собой линейные выражения.

Такие задачи часто возникают в практических ситуациях. Мы подробно рассмотрим как ставится задача линейного программирования и как применяются методы оптимизации.

Становление этого класса задач относится к 50-м годам ХХ века и связано с решением в ряде стран практических задач в экономике (наилучшая загрузка оборудования, раскрой материалов и т.д.). Рассмотрим постановки (и решения) некоторых задач.

Задача 1

Фирма планирует начать выпуск шкафов и столов для компьютеров. Исходные данные приведены в следующей таблице стандартного вида.

Ресурсы	Запасы	Расходные коэффициенты
шкафы столы
Дсп, м^2		3,5 1
Стекло, м^2		1 2
Труд, чел-часы		1 1
Прибыль, у.е.		200 10 0

Пусть х₁ – количество шкафов, х₂- количество столов

3,5 х₁ + х₂ ≤ 350

х₁ + 2х₂ ≤ 240

х₁ + х₂ ≤ 150 → ограничения модели

х₁, х₂ ≥ 0

F= 200x₁ + 100x₂ → max (целевая функция)

Смысл модели: найти такой набор переменных х₁, х₂, который удовлетворяет ограничениям и при этом обращает целевую функцию в максимум.

Сразу же покажем графоаналитический способ решения это модели.

Систему ограничений перепишем так:

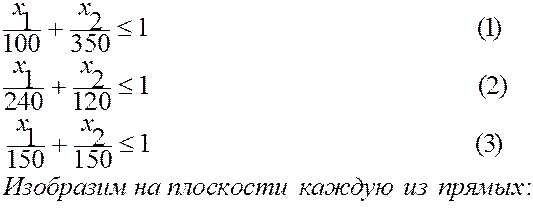
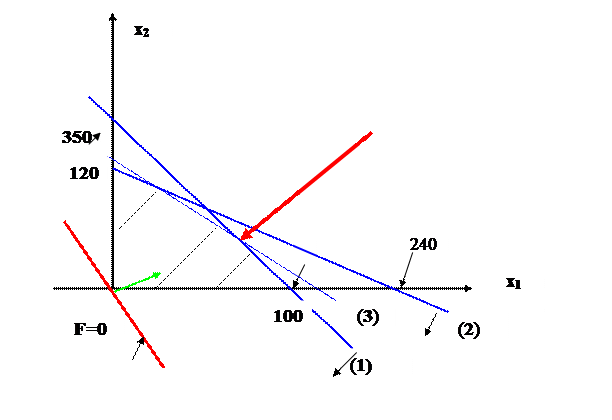
Рис. 2.1

Множество допустимых решений заштриховано на рис 2.1. Среди точек этого пятиугольника и нужно выбрать оптимальную.

Далее будет отмечено, что оптимальная точка (точка глобального максимума) совпадет хотя бы с одной угловой точкой многоугольника. Чтобы их все не перебирать поступим так:

изобразим линию уровня F=0 и отметим в начале координат вектор- градиент. Из курса высшей математики мы знаем, что он ортогонален линии уровня и указывает направление возрастания целевой функции F (даже наибольшего возрастания)- нам это и нужно – ведь речь идет о прибыли.

Дата добавления: 2015-06-04