
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приближенное вычисление определенных интегралов
|
|
|
|
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ
Разложение некоторых элементарных функций в ряд Тейлора (Маклорена).
Для разложения функции  в ряд Маклорена (8.3) нужно:
в ряд Маклорена (8.3) нужно:
а) найти производные  ;
;
б) вычислить значения производных в точке 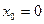 ;
;
в) написать ряд (8.3) для заданной функции и найти его интервал сходимости;
г) найти интервал 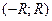 , в котором остаточный член ряда Маклорена
, в котором остаточный член ряда Маклорена 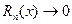 при
при  . Если такой интервал существует, то в нем функция
. Если такой интервал существует, то в нем функция  и сумма ряда Маклорена совпадают.
и сумма ряда Маклорена совпадают.
Замечание. В интервале сходимости степенного ряда остаточный член стремиться к нулю при  .
.
Приведём таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций (эти разложения следует запомнить):
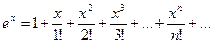 ,
,  , (8.4)
, (8.4)
 ,
,  , (8.5)
, (8.5)
 ,
,  , (8.6)
, (8.6)
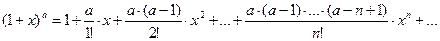 ,
,
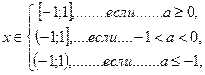 (8.7)
(8.7)
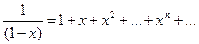 ,
, 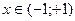 , (8.8)
, (8.8)
 ,
,  , (8.9)
, (8.9)
 ,
, 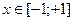 , (8.10)
, (8.10)
 , (8.11)
, (8.11)
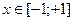 , (8.12)
, (8.12)
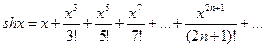 ,
,  , (8.13)
, (8.13)
 ,
,  . (8.14)
. (8.14)
Докажем формулу (8.4). Пусть 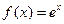 .
.
Имеем:
а)  ,
, 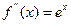 ,
, 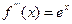 ,….,
,…., 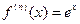 ,…….;
,…….;
б) 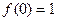 ,
,  ,
,  ,…..,
,…..,  ;
;
в) 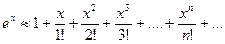 ;
; 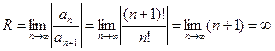 ,
,
т.е. ряд сходится в интервале  ;
;
г) для всех  имеем
имеем 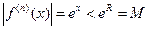 , т.е. все производные в этом интервале ограничены одним и тем же числом
, т.е. все производные в этом интервале ограничены одним и тем же числом  . Следовательно, по теореме 8.2
. Следовательно, по теореме 8.2 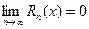 . Таким образом,
. Таким образом,  .
.
Докажем формулу (8.5). Пусть  .
.
Имеем:
а) 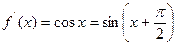 ,
, 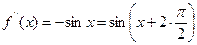 ,
,  ,
,
…., 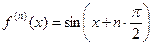 ,………….;
,………….;
б) 
в)  . Легко проверить, что полученный ряд сходится на всей числовой оси, т.е. при всех
. Легко проверить, что полученный ряд сходится на всей числовой оси, т.е. при всех 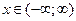 ;
;
г) любая производная функции  по модулю не превосходит единицы,
по модулю не превосходит единицы,  . Следовательно, по теореме (8.2) имеет место разложение (8.5).
. Следовательно, по теореме (8.2) имеет место разложение (8.5).
Докажем формулу (8.6). Пусть 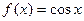 .
.
Формулу (8.6) можно доказать также, как и формулу (8.5). Однако проще получить разложение функции 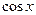 , воспользовавшись свойством 3 степенных рядов. Продифференцировав почленно ряд (8.5), получим:
, воспользовавшись свойством 3 степенных рядов. Продифференцировав почленно ряд (8.5), получим:
 ,
,  .
.
Докажем формулы (8.13) и (8.14). Пусть  (или
(или 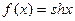 ).
).
Заменив в формуле (8.4)  на
на  , получим разложение функции
, получим разложение функции  :
:
 , (8.15)
, (8.15)
справедливое для всех 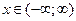 .
.
Суммируя и вычитая почленно равенства (8.4) и (8.15), получим разложение гиперболического косинуса (синуса):
 ,
,  ,
,
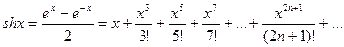 ,
,  .
.
Формулы (8.13) и (8.14) доказаны.
Докажем формулу (8.7). Пусть 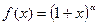 , где
, где 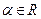 .
.
Имеем:
а)  ,
, 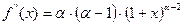 , ….,
, ….,
 , ….,
, ….,  ;
;
б) 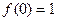 ,
, 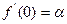 ,
, 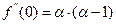 ,…..,
,….., 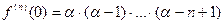 ,….;
,….;
в)  ;
;
г) 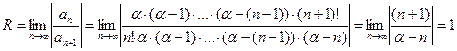 , т.е. составленный для функции
, т.е. составленный для функции  ряд сходится в интервале
ряд сходится в интервале  .
.
Можно показать, что и в данном случае, т.е. при  , остаточный член Rn(x) стремится к нулю при
, остаточный член Rn(x) стремится к нулю при  .
.
Ряд (8.7) называется биномиальным. Если 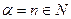 , то все члены ряда с (n + 1)-го номера равны 0, так как содержат множитель
, то все члены ряда с (n + 1)-го номера равны 0, так как содержат множитель 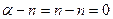 . В этом случае ряд (8.7) представляет собой известную формулу бинома Ньютона:
. В этом случае ряд (8.7) представляет собой известную формулу бинома Ньютона:
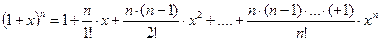 .
.
Докажем формулу (8.8). Пусть  .
.
Формула (8.8) может быть получена разными способами:
1) пользуясь правилом разложения функции в ряд;
2) рассматривая ряд 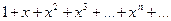 как ряд геометрической прогрессии, первый член которой равен единице и знаменатель q = х; известно (см. пример 7.1), что данный ряд сходится при
как ряд геометрической прогрессии, первый член которой равен единице и знаменатель q = х; известно (см. пример 7.1), что данный ряд сходится при  и его сумма равна
и его сумма равна  ;
;
3) воспользовавшись формулой (8.7): положив в ней 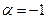 и заменив х на - х, получим формулу (8.8).
и заменив х на - х, получим формулу (8.8).
Докажем формулу (8.9). Пусть 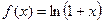 .
.
Формула (8.9) также может быть доказана разными способами. Приведем один из них.
Рассмотрим равенство
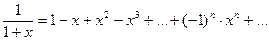 ,
,
справедливое для всех  . Используя свойство 4 степенных рядов, проинтегрируем данный ряд на отрезке [0; x ],
. Используя свойство 4 степенных рядов, проинтегрируем данный ряд на отрезке [0; x ],  :
:
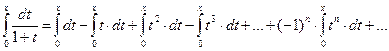 ,
,
или
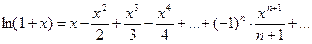
Можно показать, что это равенство справедливо и для х = 1.
Докажем формулу (8.10). Пусть  .
.
Положив в формуле (8.7) 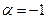 и заменив х на х 2, получим равенство
и заменив х на х 2, получим равенство
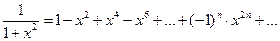 ,
,  .
.
Тогда:
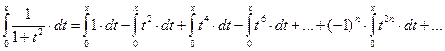 ,
,
или

Можно показать, что равенство справедливо и при х = ±1, т. е. при всех  .
.
Докажем формулу (8.12). Пусть  .
.
Положив в формуле (8.7)  и заменив х на (- х 2), получим равенство
и заменив х на (- х 2), получим равенство
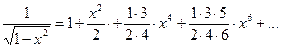 ,
,  .
.
Тогда
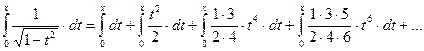 ,
,
или

Можно показать, что полученное равенство справедливо при всех  .
.
Ряды (8.4)-(8.14) в комбинации с правилами сложения, вычитания, умножения, дифференцирования, интегрирования степенных рядов (см. свойства степенных рядов) могут быть использованы также при разложении некоторых других функций в ряд Маклорена (Тейлора).
Пример 8.1. Разложить в ряд Маклорена функцию 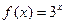 .
.
Решение:
Так как 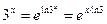 , то, заменяя
, то, заменяя  на
на 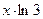 в разложении (8.4), получим:
в разложении (8.4), получим:
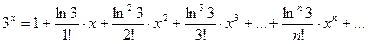 ,
,  .
.
Пример 8.2. Выписать ряд Маклорена функции 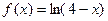 .
.
Решение: Так как
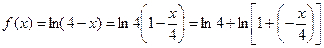 ,
,
то, воспользовавшись формулой (8.9), в которой заменим  на
на  , получим:
, получим:
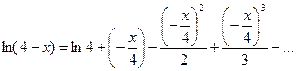 ,
,
или 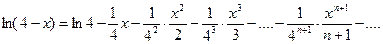 ,
,
если 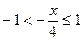 , т.е.
, т.е.  .
.
Пример 8.3. Разложить в ряд Маклорена функцию 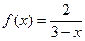 .
.
Решение: Воспользуемся формулой (8.8). Так как
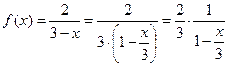 ,
,
то, заменив  на
на  в формуле (8.8), получим:
в формуле (8.8), получим:
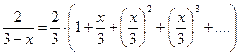 ,
,
или
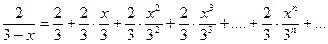 ,
,
где  , т.е.
, т.е.  .
.
9.1. Приближённые вычисления значений функции.
Пусть требуется вычислить значение функции  при
при  с заданной точностью
с заданной точностью 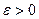 .
.
Если функцию  в интервале
в интервале  можно разложить в степенной ряд
можно разложить в степенной ряд

и 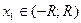 , то точное значение
, то точное значение 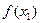 равно сумме этого ряда при
равно сумме этого ряда при  т. е.
т. е.
 ,
,
а приближенное значение, - частичной сумме 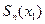 , т.е.
, т.е.
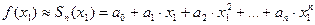 .
.
Точность этого равенства увеличивается с ростом п. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т. е.
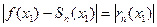 ,
,
где

Таким образом, ошибку  можно найти, оценив остаток
можно найти, оценив остаток 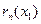 ряда.
ряда.
Для рядов лейбницевского типа
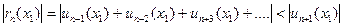 (см. п. 6.1).
(см. п. 6.1).
В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммировался. В качестве оценки 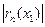 берут величину остатка этого нового ряда.
берут величину остатка этого нового ряда.
Пример 9.1. Найти sin 1 с точностью до 0,001.
Решение: Согласно формуле (8.5),
 .
.
Стоящий справа ряд сходится абсолютно (проверить самостоятельно). Так как 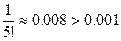 а
а 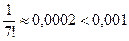 , то для нахождения sin 1 с точностью до 0,001 достаточно первых трех слагаемых:
, то для нахождения sin 1 с точностью до 0,001 достаточно первых трех слагаемых:
 .
.
Допускаемая при этом ошибка меньше, чем первый отброшенный член (т.е. меньше, чем 0,0002). Вычисленное микрокалькулятором значение sin 1 примерно равно 0,84147.
Пример 9.2. Вычислить число  с точностью до 0,001.
с точностью до 0,001.
Решение: Подставляя х = 1 в формулу (8.4), получим:
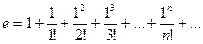
Справа стоит знакоположительный ряд. Возьмем п слагаемых и оценим ошибку  :
:

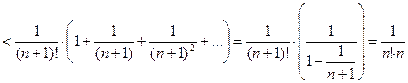 ,
,
т.е. 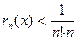 . Остается подобрать наименьшее натуральное число п, чтобы выполнялось неравенство
. Остается подобрать наименьшее натуральное число п, чтобы выполнялось неравенство 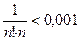 .
.
Нетрудно вычислить, что это неравенство выполняется при 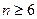 . Поэтому имеем:
. Поэтому имеем:
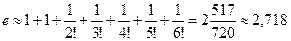 .
.
Замечание. Оценку остатка ряда можно производить с помощью остаточного члена ряда Маклорена
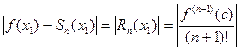 ,
,
где с находится между 0 и  . В последнем примере
. В последнем примере  ,
,  . Так как
. Так как  , то
, то 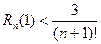 . При
. При 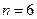 имеем:
имеем:
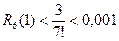 ,
,  .
.
Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции (см. [1] р.7 или [2] р.4), либо нахождение первообразной сложно.
Пусть требуется вычислить 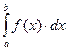 с точностью до
с точностью до 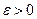 . Если подынтегральную функцию f(x) можно разложить в ряд по степеням х и интервал сходимости
. Если подынтегральную функцию f(x) можно разложить в ряд по степеням х и интервал сходимости  включит в себя отрезок
включит в себя отрезок 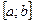 , то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.
, то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.
Пример 9.3. Вычислить интеграл  с точностью до
с точностью до 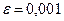 .
.
Решение: Разложим подынтегральную функцию в ряд Маклорена, заменяя х на (- х2) в формуле (8.4):
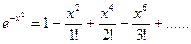 ,
,  . (9.1)
. (9.1)
Интегрируя обе части равенства (9.1) на отрезке  , лежащем внутри интервала сходимости
, лежащем внутри интервала сходимости  , получим:
, получим:


Получили ряд лейбницевского типа. Так как  , а
, а 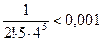 ,
,
то с точностью до 0,001 имеем:
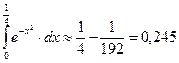 .
.
Замечание. Первообразную F(x) для функции  легко найти в виде степенного ряда, проинтегрировав равенство (9.1) в пределах от 0 до х:
легко найти в виде степенного ряда, проинтегрировав равенство (9.1) в пределах от 0 до х:
 ,
,  .
.
Функции 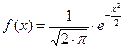 и
и  играют очень важную роль в теории вероятностей. Первая - плотность стандартного распределения вероятностей, вторая - функция Лапласа
играют очень важную роль в теории вероятностей. Первая - плотность стандартного распределения вероятностей, вторая - функция Лапласа 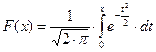 (или интеграл вероятностей). Мы получили, что функция Лапласа представляется рядом
(или интеграл вероятностей). Мы получили, что функция Лапласа представляется рядом
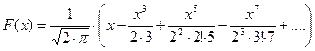 ,
,
который сходится на всей числовой оси.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2131; Нарушение авторских прав?; Мы поможем в написании вашей работы!