Способ последовательного дифференцирования

Приближенное решение дифференциальных уравнений

Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения уравнения можно воспользоваться рядом Тейлора.

Познакомимся с двумя способами решения дифференциальных уравнений с помощью степенных рядов.

Пусть, например, требуется решить уравнение

у" = f(x;y;y'), (9.2)

удовлетворяющее начальным условиям

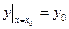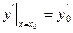, . (9.3)

Решение у = у(х) уравнения (9.2) ищем в виде ряда Тейлора:

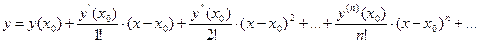, (9.4)

при этом первые два коэффициента находим из начальных условий (9.3). Подставив в уравнение (9.2) значения , , 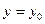, 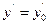находим третий коэффициент: 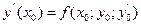. Значения 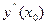, ,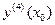..... находим путем последовательного дифференцирования уравнения (9.2) по 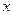и вычисления производных при 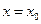. Найденные значения производных (коэффициентов) подставляем в равенство (9.4). Ряд (9.4) представляет искомое частное решение уравнения (9.2) для тех значений х, при которых он сходится. Частичная сумма этого ряда будет приближенным решением дифференциального уравнения (9.2).

Рассмотренный способ применим и для построения общего решения уравнения (9.2), есл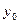и и 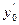рассматривать как произвольные постоянные.

Способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.

Пример 9.4. Методом последовательного дифференцирования найти пять первых членов (отличных от нуля) разложения в ряд решения уравнения

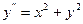, при начальных условиях: , .

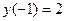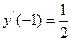Решение: Будем искать решение уравнения в виде

.

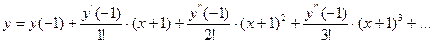Здесь 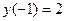, 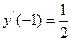. Находим у" (-1), подставив х = - 1 в исходное уравнение: у" (-1) = (-1)² + 2² = 5. Для нахождения последующих коэффициентов дифференцируем заданное дифференциальное уравнение:

,

,

,...

……………………….

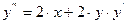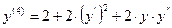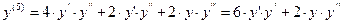При х = - 1 имеем:

,

,

,...

……………………….

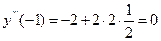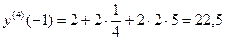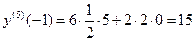Подставляя найденные значения производных в искомый ряд, получим:

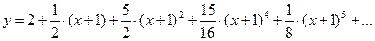
Дата добавления: 2015-06-04