Прогнозирование

Под прогнозированием (в широком смысле) понимают предска­зание поведения и характеристик системы в будущем на основе наших знаний о настоящем и прошлом системы, или, как часто говорят, пред­ыстории. Под прогнозированием (в узком смысле) понимают предска­зание значений входных параметров системы, т.е. характеристик внеш­ней среды или системы в целом. В дальнейшем мы не будем разделять эти понятия, так как в каждом конкретном случае из контекста будет яс­но, что мы имеем в виду.

В простейшем случае прогнозирование основано только на имею­щих­ся данных и проводится лишь один раз. Однако на практике часто от мо­мента при­нятия решения до осуществления операции проходит зна­чи­тель­ное вре­мя, за которое си­туа­ция может заметно измениться. По­это­му разработан ряд методов, пре­дусматривающих возможность по мере по­ступления информации об из­ме­не­нии значений входных параметров кор­ректировать выбор варианта операции.

Важнейшим параметром прогноза является время упреждения, от кото­ро­го сильно зависит надежность (точность) прогноза и дру­гие пара­мет­ры модели. Под временем упреждения понимают величину интер­ва­ла времени между мо­мен­том завершения операции и моментом при­ня­тия решения. Естественно, что, чем больше время упреждения, тем ме­нее на­дежен прогноз и больше не­об­хо­димость его уточнения по мере по­ступ­ления новой информации. Для этого вре­мя упреждения разбивается на n временных интервалов, которые опре­де­ля­ют величину промежутков вре­мени между измерениями входных переменных с целью проверки и уточнения ранее сделанных прогнозов. Величина этих временных интер­валов зависит от характера и от скорости изменения измеряемых вход­ных переменных.

Таким образом, исходные данные часто представляют собой ряд последовательно во времени измеренных значений переменных, которые в литературе называют временными рядами.

Можно выделить два вида прогнозируемых характеристик систе­мы, зависящих от времени: переменные состояния и переменные интен­сивности. Переменная состояния определяется периодически, и ее зна­чение в течение небольшого интервала времени не зависит от времени, прошедшего с момента начала наблюдения. Переменная интенсивнос­ти также определяется периодически, но ее значение пропорционально времени, прошедшему с момента предыдущего наблюдения. Такие ха­рактеристики системы, как температура, скорость, цена являются приме­рами переменной состояния. Примерами переменной интенсивности яв­ляются количество выпавших осадков, проданных экземпляров изделия, спрос и т.п.

Если переменная состояния характеризует количество, то пере­менная интенсивности - скорость его изменения.

Процессы прогнозирования переменных состояния и интенсивнос­ти отличаются друг от друга следующими особенностями:

1) Если измерения характеристик проводятся через разные ин­тервалы времени, то величину интервала необходимо учиты­вать только при оценке переменных интенсивности;

2) Правильный прогноз переменной состояния должен опреде­лять ее значение в конце времени упреждения, а прогноз пере­менной интенсивности должен представлять собой сумму прогнозов на протяжении времени упреждения;

3) Функция распределения во времени вероятностей ошибок прогноза для переменной состояния соответствует функции распределения вероятностей ошибок в исходных данных;

4) для переменной интенсивности закон распределения вероят­ностей ошибок прогноза во времени стремится к нормальному при любом законе распределения вероятностей ошибок в исходных данных, так как эти ошибки представляют собой сумму ошибок прогноза в отдельные интервалы времени.

Методы прогнозирования могут быть разделены на три группы: статистические (описательные), причинно-следственные и комбини­рованные.

Для изучения исследуемого процесса следует задать закон измене­ния входных переменных во времени. Выходные переменные системы могут быть описаны с помощью некоторой модели. По такой модели, включающей описание предыстории системы, прогноз можно составить путем расчета состояния системы для некоторого будущего момента вре­мени. Если удается построить модель окружающей среды, позволяющую выявить причины изменений в системе (вторая группа методов), то прог­ноз, полученный с помощью такой модели, объясняет будущее системы.

Прогнозы на основе анализа причинно-следственных связей ис­пользуются главным образом для предсказания моментов появления экс­тремумов в рассматриваемой временной зависимости переменных систе­мы и значений переменных в экстремальных точках. Пример такого прогноза представляют кривые жизненного цикла любой продукции.

Спрос на любую продукцию имеет фазы начального роста, наи­высшего уровня и спада. Во время последней фазы продукция исчезает с рынка. Подобные модели точно описывают историю спроса на продук­цию, но не дают достаточно твердой основы для предсказания момента перехода из одной фазы спроса в другую.

Статистический прогноз в лучшем случае позволяет делать ве­роятностные утверждения о возможных появлениях экстремумов в рас­сматриваемой временной зависимости переменных системы и о значе­ниях переменных в экстремальных точках.

В задачах прогнозирования предполагают, что в момент времени T задана последовательность результатов наблюдений 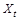для некоторого множества моментов времени 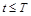. Прогнозирующая модель задает множество выходных переменных 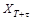, где t>0 - время упреждения. В общем виде выражение для модели можно записать в виде

,

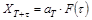где вектор 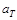представляет собой коэффициенты модели, получаемые по результатам наблюдений до момента T включительно, а матрица F - на­бор аппроксимирующих функций. Строки матрицы соответствуют эле­ментам модели, а столбцы – моментам времени. В большинстве практи­ческих приложений F определяет время относительно момента самого последнего наблюдения, а значения коэффициентов a зависят от выбора начала отсчета времени.

Весьма общий и, пожалуй, наиболее распространенный класс мо­делей составляют полиномиальные, т.е. такие модели которые могут быть представлены с помощью вещественных полиномов

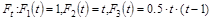и т.д.

Математические методы позволяют представить прогнозирующую модель в виде полинома любого порядка. Однако обычно в экономичес­ких задачах нет необходимости в использовании полиномов высокого по­рядка. Довольно часто для анализа локальных изменений в наблюдаемых данных достаточно использовать полином первой степени (прямую ли­нию). Подгонка прямой линии для конкретного ряда прогнозируемых данных производится путем варьирования величины второго коэффи­циента, отражающего тенденцию изменения временного ряда за длитель­ный период времени (вековой тренд). Если величина этого коэффициен­та мала, то и его можно исключить из модели.

На практике часто встречаются периодические процессы. Так, на­пример, спрос на некоторую продукцию может меняться по циклам, пов­торяющимся каждый торговый сезон. Включение подобных периодичес­ких (сезонных) колебаний в модель повышает эффективность прогноза и позволяет лучше предсказывать ожидаемые высокие и низкие значения прогнозируемых переменных. Соответствующие модели называются сезонными моделями.

Основной подход в сезонных моделях заключается в пред­став­ле­нии циклических изменений прогнозируемой переменной рядами Фурье

,

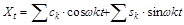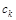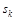где и - коэффициенты, полученные по исходным данным с помо­щью соответствующей регрессии, w=2p¤f - основная частота, f - чис­ло наблюдений в одном сезонном цикле, t - время, за которое должен быть выдан прогноз, а суммирование ведется по всем частотам вплоть до час­тоты Найквиста (наивысшей частоты гармонического разложения диск­ретного ряда, которая определяется половиной интервала между наблю­дениями).

Строгая периодичность в реальных задачах встречается редко. В общем случае необходимо использовать модели, предусматривающие со­четание полиномиальных трендов и циклических изменений.

На практике подобные модели оказываются слишком сложными для ручного счета. Поэтому существуют специальные пакеты программ для ЭВМ, при работе с которыми большинство пользователей не испыты­вают необходимости в понимании существа вычислительных процедур.

В вероятностных моделях наиболее часто используется предпо­ложение о том, что наблюдаемые величины принадлежат некоторому распределению (вид его задается), а параметры этого распределения и их изменение во времени нужно определить.

Другим вероятностным представлением является модель в виде частотного распределения с параметрами для относительной частоты наблюдений, попадающих в j -й интервал. При этом, если в течение при­нятого времени упреждения не ожидается изменения распределения, то решение принимается на основании измеренного эмпирического частот­ного распределения.

Дата добавления: 2015-06-04