
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аксиомы теории принятия решений
|
|
|
|
Теория принятия решений
Лекция № 14
Субъективная вероятность
На практике часто нет достаточной информации о вероятностях и получение ее сопряжено с большими затратами средств и времени или вообще не представляется возможным. В таких случаях вместо объективной вероятности, вводимой как результат соответствующих измерений, используют субъективную вероятность. Субъективная вероятность измеряет степень уверенности «разумного» индивидуума в справедливости утверждения, вероятность которого определяется. При этом не исключается, что два «разумных» индивидуума могут иметь разную степень уверенности в справедливости одного и того же утверждения.
Разработка теории предпочтений для принятия решений в условиях неопределенности привела к созданию моделей ожидаемой полезности, в которых субъективные вероятности последствий различных способов действий и полезность получаются из аксиом предпочтений. Каждая такая модель включает процедуры измерения и «настройки» на определенное лицо и учет его субъективных пристрастий и установок.
Теория принятия решений представляет собой набор понятий и систематических методов, позволяющих всесторонне анализировать проблемы принятия решений в условиях неопределенности. В основе логических построений этой теории лежит ряд аксиом. Если лицо, принимающее решения, рассматривает эти аксиомы как руководство к действию, т.е. считает их разумными, то оно должно принимать решения, следуя результатам, полученным из теории.
В основе теории принятия решений лежит предположение о том, что выбор альтернатив должен определяться двумя факторами:
1) представлениями лица, принимающего решение, о вероятностях различных возможных исходов (последствий), которые могут иметь место при выборе того или иного варианта решения;
2) предпочтениями, отдаваемыми им различным возможным исходам.
Теория принятия решений предписывает лицу, принимающему решение, нормы поведения, которым он должен следовать, чтобы не вступить в противоречие со своими собственными суждениями и предпочтениями.
Прежде, чем сформулировать аксиомы, введем принятые в этой теории обозначения и определения.
Простой лотереей  назовем вероятностное событие, имеющее два возможных исхода
назовем вероятностное событие, имеющее два возможных исхода  и
и  , вероятности наступления которых равны p и (1-p), соответственно.
, вероятности наступления которых равны p и (1-p), соответственно.
Символами  будем, как и прежде, обозначать отношения строгого предпочтения, эквивалентности и нестрогого предпочтения, соответственно. Например, запись
будем, как и прежде, обозначать отношения строгого предпочтения, эквивалентности и нестрогого предпочтения, соответственно. Например, запись 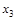 ~
~  означает, что исход
означает, что исход 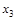 эквивалентен лотерее
эквивалентен лотерее  .
.
Аксиома 1. Существование относительных предпочтений.
Для любой пары исходов  и
и  выполняется одно из соотношений предпочтения:
выполняется одно из соотношений предпочтения:
 ~
~  , или
, или  f
f  , или
, или  f
f  .
.
Аксиома 2. Транзитивность.
Для любых лотерей 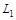 ,
,  и
и 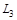 справедливы следующие утверждения:
справедливы следующие утверждения:
а) если 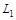 ~
~  и
и  ~
~ 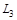 , то
, то 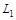 ~
~ 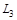 ;
;
в) если 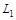 f
f  и
и  ~
~ 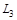 , то
, то 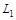 f
f 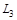 и т.д.
и т.д.
Поскольку исход можно интерпретировать как случай вырожденной лотереи (при p=1), то аксиомы 1 и 2 вместе означают, что лицо, принимающее решения, может произвести ранжирование относительного предпочтения различных возможных исходов. Пусть 
 - исход, который не является более предпочтительным, чем любой другой, а
- исход, который не является более предпочтительным, чем любой другой, а 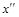 - исход, который не является менее предпочтительным, чем любой другой. Тогда для всех допустимых x выполняются соотношения
- исход, который не является менее предпочтительным, чем любой другой. Тогда для всех допустимых x выполняются соотношения  , т.е.
, т.е.  и
и 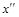 означают соответственно наименее и наиболее предпочтительные исходы. Следует отметить, что это могут быть гипотетические исходы.
означают соответственно наименее и наиболее предпочтительные исходы. Следует отметить, что это могут быть гипотетические исходы.
Аксиома 3. Сравнение простых лотерей.
Если для лица, принимающего решения,  f
f  , то
, то

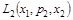 при
при 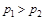 ;
;

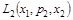 при
при 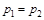 .
.
Аксиома 4. Численная оценка предпочтений.
Каждому возможному исходу x лицо, принимающее решения, может поставить в соответствие число 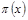 (где
(где 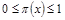 ), такое, что
), такое, что
x ~  .
.
Аксиомы 3 и 4 определяют для лица, принимающего решения, меру относительного предпочтения различных исходов 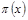 , называемую вероятностью предпочтения.
, называемую вероятностью предпочтения.
Аксиома 5. Численная оценка неопределенности суждений.
Каждому возможному событию E, которое может влиять на исход решения, можно поставить в соответствие число P(E), где 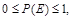 такое, что становятся равноценными лотерея
такое, что становятся равноценными лотерея  и ситуация, при которой лицо, принимающее решения, получает
и ситуация, при которой лицо, принимающее решения, получает  , если происходит событие E, и
, если происходит событие E, и 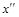 , если событие E не происходит. Значение P(E) определяется лицом, принимающим решения.
, если событие E не происходит. Значение P(E) определяется лицом, принимающим решения.
Аксиома 6. Возможность замены.
Если модифицировать задачу принятия решения путем замены одного исхода (или лотереи) другим исходом (или лотереей), которые равноценны для лица, принимающего решение, то обе задачи (старая и модифицированная) будут равноценны для этого лица.
Аксиома 7. Эквивалентность условного и безусловного предпочтений.
Пусть 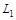 и
и  - лотереи, возможные только при наступлении события Е. Если известно, наступит событие Е или нет, то лицо, принимающее решение, должно иметь те же предпочтения между
- лотереи, возможные только при наступлении события Е. Если известно, наступит событие Е или нет, то лицо, принимающее решение, должно иметь те же предпочтения между 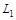 и
и  , как и при отсутствии этой информации.
, как и при отсутствии этой информации.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2256; Нарушение авторских прав?; Мы поможем в написании вашей работы!