Предпочтение и полезность

Хотя теоретические построения предполагают определенные структурные свойства у изучаемых объектов, теория предпочтений исхо­дит только из двух гипотез.

Во-первых, предполагается, что множество вариантов решения, стратегий или способов поведения не является пустым. Часто это множество содержит недопустимые альтернативы вследствие, например, того, что трудно идентифицировать все допустимые альтернативы с по­мощью какой-либо простой процедуры, или потому, что некоторые недо­пустимые альтернативы могут потребоваться при измерении или масшта­бировании полезности.

Во-вторых, предполагается бинарность предпочтений, что нахо­дит выражение во введении отношения «предпочтение - или - безраз­ли­чие» (нестрогого предпочтения) на множестве альтернатив.

Бинарное отношение является фундаментальным понятием теории предпочтений, поэтому изложим некоторые положения теории бинарных отношений.

Бинарное отношение R на непустом множестве X есть подмно­жество всех упорядоченных пар элементов из X. Множествовсех упорядоченных пар задается прямым произведением

Запись 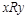(читается " x находится в отношении R к y") означает, что пара (x,y) принадлежит R. Аналогично не 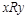(записывается как 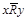) означает что x не находится в отношении R к y, а пара (x,y) не принадлежит R.

Пусть x, y и z являются элементами множества X. Тогда для би­нар­ного отношения R можно ввести восемь свойств, которые обычно разделяют на четыре группы.

I. Рефлексивность и нерефлексивность.

Бинарное отношение R на множестве X является рефлексивным, если для каждого 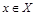; нерефлексивным, если 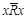для каждого .

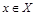II. Симметричность и асимметричность.

Бинарное отношение R на множестве X является симметричным, если из 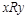следует 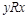; асимметричным, если из 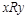следует .

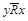III. Транзитивность и отрицательно транзитивность.

Бинарное отношение R на множестве X является транзитивным, если из 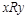и 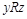следует 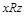; отрицательно транзитивным, если из 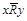и 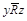следует .

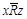IY. Связность и слабая связность.

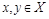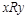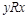Бинарное отношение R на множестве X является связным (сильно связным или полным), если для любых выполняется или ; слабосвязным, если из 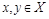и 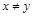следует 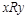или .

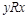Слабосвязное отношение иногда называют полным или прос­то связным.

Два свойства первой группы являются противоречивыми, т.е. не мо­гут выполняться одновременно, но этого нельзя утверждать отно­си­тель­но свойств остальных трех групп. Например, асимметричность и от­ри­ца­тель­ная транзи­тив­ность означают транзитивность; связность влечет сла­бую связность. Сим­мет­рич­ность и асимметричность имеют место од­но­вре­менно, если R пусто; если же R не пусто, то эти свойства являются противоречивыми.

Транзитивное бинарное отношение называется упорядочением или отношением порядка.

Пример

Пусть X - множество всех людей.

Отношение «выше, чем» яв­ляется нерефлексивным, асимметрич­ным, транзитивным и отрицательно транзитивным.

В теории предпочтений используются два основных бинарных от­но­шения на множестве X: отношение предпочтения 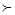и нестрогого предпочтения .

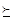Запись 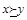читается «x предпочтительнее, чем y, либо безраз­ли­чен к y»; иногда пользуются формулировкой «y не предпочтительнее, чем x». Запись 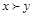читается «x предпочтительнее, чем y».

Выбрав одно из отношений предпочтения в качестве основного на мно­жестве X, не­слож­но ввести и другое. Что взять в качестве основного бинарного отношения зависит от личных вкусов исследователя.

Для того, чтобы отношение предпочтения являлось упоря­до­че­ни­ем, необ­хо­дима его транзитивность, что кажется разумным.

Несмотря на очевидную разумность предположения о транзитив­нос­ти пред­почтений, имеется достаточно много примеров, из которых вид­но, что здра­вомыслящие люди могут иметь нетранзитивные пред­поч­те­ния в некоторых ситуациях. Альтернативы, используемые для ил­люст­ра­ции этого факта, обычно включают несколько критериев или харак­тер­ных признаков.

Пример

Пусть молодому ученому предлагается выбрать место работы из сле­дую­щих альтернатив:

x: ассистента в очень известном университете с окладом 3500 $;

y: доцента в университете штата N с окладом 3800 $;

z: профессора в малоизвестном колледже с окладом 4100 $.

Ученый считает, что , рассудив, что престиж стоит боль­ше, чем 300 $, но, сравнивая x и z, он чувствует, что зани­мае­мый пост и величина оклада перевешивают престижность, и полагает, что 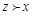. Таким об­ра­зом, в описанной ситуации его предпочтения образуют цикл

.

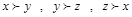Приведенный пример хорошо иллюстрирует проблему, возникаю­щую в теории выбора, а именно то, что бинарное отношение не дает путеводной нити для выхода из цикла, т.е. не позволяет сделать выбор между x, y и z, когда каж­дая альтернатива менее предпочтительна, чем некоторая другая. Здесь нет са­мой предпочтительной альтернативы.

Отношение безразличия тоже может быть как транзитивно, так и не тран­зи­тивно на X.

В случае, если предпочтения не образуют циклов, а безразличие не пред­по­лагается транзитивным, каждое непустое конечное множество X содержит максимально предпочитаемую альтернативу, т.е. одна из аль­тер­натив не менее предпочтительна, чем любая другая из данного мно­жест­ва. В этом случае са­мую предпочтительную альтернативу можно вы­делить с помощью некоторого численного представления предпочте­ний, при котором 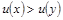, если .

Численное представление предпочтений - функцию 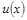назы­ва­ют полезностью.

Говорят, что бинарное отношение f является слабым упорядо­че­нием, если отношения f и ~ транзитивны.

Пусть на множестве X отношение f является слабым упорядо­че­нием. Тогда, поскольку отношение ~ транзитивно, оно является отноше­нием экви­ва­лентности (транзитивным, симметричным, рефлексивным) и, следовательно, может быть использовано для разделения (разбиения) мно­жества X на классы эквивалентности, или классы безразличия. Такие классы представляют собой непустые множества на X,причем, если A и B - два различных класса и xÎA, а yÎB, то x~y тогда и только тогда, когда A=B; если же , то 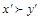для любых .

Пусть u - вещественная функция, определенная на X.

Функция u называется функцией полезности для X, если 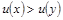для любых x и y, таких, что .

Функция u называется совершенной функцией полезности для отно­ше­ния предпочтения f на X, если для всех x и y из X справедливо неравенство 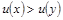тогда и только тогда, когда .

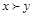Пусть отношение f на X является слабым упорядочением, для ко­торого определена совершенная функция полезности u. Тогда x~y, если и только . Отсюда следует, что классы безразличия на X совпадают с под­мно­жествами альтернатив, имеющими равную полез­ность. Экономисты иногда используют термин «карта безразличия», или «карта обмена», понимая под этим набор классов безразличия.

Множество X называется исчислимым, если оно конечно или счетно (т.е. его элементам можно поставить во взаимно однозначное со­ответствие натуральные числа).

Неисчислимым называется множество, которое не является ис­чис­лимым, т.е. ни конечным, ни счетным.

Пусть множество X исчислимо. Тогда для отношения f наXфункция полезности существует тогда и только тогда, когда отноше­ние f ациклично (т.е. нет такого набора 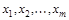из X, для которого выполняется ).

Совершенная функция полезности для отношения f наXсу­щест­вует тогда и только тогда, когда отношение f - слабое упорядочение.

Если отношение f является слабым упорядочением, функция по­лезности наXсуществует тогда и только тогда, когда существует совершенная функция полезности для отношения f наX, причем это утверждение справедливо для множества X любых размеров (исчислимо­го или неисчислимого).

Если u - совершенная функция полезности для отношения пред­поч­тения f на X, некоторая функция v также является совершенной функ­цией полезности для отношения пред­поч­тения f на X тогда и только тогда, когда для любых x и y из X неравенство 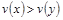справедливо тогда и только тогда, когда

.

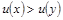Пример.

Пусть

Тогда u и v - совершенные функции полезности отношения f на X. То, что в одном случае полезность y равна 99, а в другом случае только 1, не имеет принципиального значения.

Дата добавления: 2015-06-04