Игры n лиц

В играх n лиц, как и в играх двух лиц с ненулевой суммой, разли­чают кооперативные игры и игры без кооперации.

Если кооперация запрещена, то игра n лиц очень похожа на игру двух лиц.

В кооперативных играх n лиц главное – это формирование коали­ций, а не поиск стратегий в самой игре. Такие игры обычно изучают в фор­ме характеристической функции.

По существу, характеристическая функция указывает, какую по­лез­ность чле­ны коалиции могут себе гарантировать (если коалиция сфор­ми­рована). При этом предполагается, что полученную полезность можно поделить между чле­на­ми коалиции любым желаемым способом (условие побочных платежей).

Обозначим через 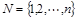множество игроков в игре n лиц. Тог­да характеристической функцией называется функция v, которая каж­дому подмножеству 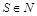ставит в соответствие действи­тель­ное число v(S) и удовлетворяет условиям

.

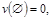
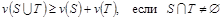Второе условие, известное как супераддитивность функции, иног­да за­ме­няют более слабым

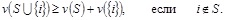
Игру отождествляют с функцией v. Элементы множества N – это игроки, а непустые подмножества из N называются коалициями.

Дележом для игры n лиц с характеристической функцией v на­зы­вается вектор 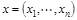, удовлетворяющий условиям

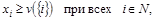
Из определения характеристической функции следует, что

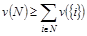. (1)

Если в формуле (1) имеет место равенство, то игра имеет только один дележ, и такую игру будем называть несущественной, так как фор­ми­рование коалиций в ней не имеет значения. Если в формуле (1) вы­пол­няется строгое не­ра­венство, то игра называется существенной и в ней су­щест­вует бес­ко­неч­ное количество дележей.

S-эквивалентная нормализация.

Две игры u и v называются S-эк­ви­ва­лентными, если существует строго положительное число α>0 и вектор 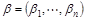, такие, что для любого 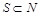справедливо равенство

.

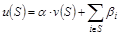Все свойства допустимого решения сохраняются при S -эквива­лент­ности. Таким образом, достаточно изучить по одной игре для каж­дого S -эквивалент­но­го класса.

Игра v нормализована в форме (0,1), если

.

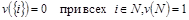Теорема. Любая существенная игра S - эквивалентна одной и толь­ко одной игре в нормализованной (редуцированной) форме (0,1).

Эта теорема позволяет ограничиться рассмотрением только (0,1) нормали­зованных игр.

Пусть задана игра v. Будем говорить, что дележ x доминирует другой дележ y (обычно обозначается как 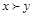), если существует не­пус­тое мно­жес­т­во 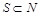, такое, что

.

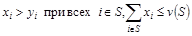Ядром игры называется множество всех недоминируемых де­ле­жей.

К сожалению, широкий класс игр имеет пустое ядро.

Устойчивым множеством (решением фон Неймана - Морген­штерна) на­зывается множество дележей V такое, что:

а) из 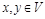следует, что 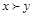не может иметь места;

б) если z является дележом, но 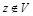, то существует платеж 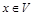такой, что .

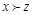Следует отметить, что, хотя большинство игр имеет много устой­чи­вых множеств, существуют игры, у которых нет устойчивых множеств.

В общем случае ядро является подмножеством каждого устой­чи­вого множества.

Если же ядро само устойчиво, то оно представляет собой един­ст­венное устойчивое множество.

Значением игры по Шепли является априорное матема­ти­чес­кое ожи­да­ние выигрыша, который игрок предполагает получить, участ­вуя в игре.

Значение игры по Шепли вводится аксиоматически как отобра­же­ние мно­жества игр n лиц на множество n -мерных векторов (платежей), которое име­ет следую­щие свойства: симметрия (если игра симметрична, ее значение дол­жно быть симметрично); эффективность (множество всех игроков, которые делают вклады для участия в игре, полностью отоб­ражается во множество пла­те­жей, получаемых игроками); аддитив­ность (значение суммы двух игр равно сумме их значений). Можно доказать, что только одно значение игры удовлетворяет аксиомам Шепли, а именно вектор 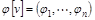, задаваемый формулой

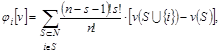
где s и n - числа игроков в S и N соответственно.

Множество сделок представляет собой еще один подход к пост­рое­нию устойчивых множеств. При этом предполагается, что коа­лиции сфор­ми­рованы, после чего рассматриваются векторы выигры­шей, кото­рые бу­дут ус­тойчивыми в особом смысле: ни одному игроку нельзя пригрозить так, чтобы в результате уменьшилась его доля выиг­рыша.

Коалиционной структурой в игре n лиц называется разбиение мно­жест­ва игроков N на взаимно непересекающиеся подмножества, объединение ко­то­рых дает N:

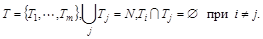
Индивидуально-рациональной конфигурацией выигрыша на­зы­вает­ся пара 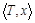, где T – коалиционная структура, а 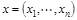- вектор, удов­летворяющий условиям

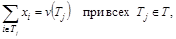
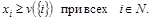
Если T – коалиционная структура и 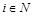, то партнерами игрока i в T является множество игроков 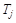, такое, что 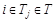. Записывается это в виде .

Пусть 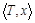- индивидуально-рациональная конфигурация и k и l явля­ются партнерами в T. Тогда угрозой игрока k против lназывается другая индивидуально-рациональная конфигурация такая, что

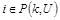а) если , то ;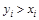

б) .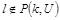

Контругрозой игрока l против k называется некоторая третья инди­ви­дуально-рациональная конфигурация 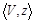, такая, что

а) если 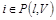, то ,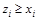

б) если 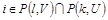, то ,

в) .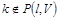

Индивидуально-рациональная конфигурация выигрыша, при кото­рой для каждой угрозы kпротив l у игрока l имеется контругроза против k, называется устойчивой.

Множеством сделок 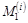называется множество всех устойчи­вых ин­ди­ви­дуально-рациональных конфигураций выигрыша.

Это множество не пусто в строгом смысле, т.е. для любой коали­цион­ной структуры T существует по крайней мере один дележ x, такой, что .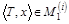

Различные множества сделок можно получить, изменяя виды уг­роз. Так, например, можно вводить в рассмотрение угрозы одной группы игроков против некоторой другой группы или угрозы отдельного игрока против некоторого иг­рока, который не является его партнером по коалиции.

Дата добавления: 2015-06-04