Смешанные стратегии

Лекция № 10

Большинство матричных игр не имеет седловых точек. В такой ситуации игроку важно, чтобы противник не угадал, какую стратегию он будет использовать. Для осуществления этого плана следует пользовать­ся смешанной стратегией. Смешанная стратегия представляет собой схему случайного выбора чистой стратегии. Математически ее можно представить как вероятностное распределение на множестве чистых стра­тегий игрока.

Def. Пусть R – платежная матрица игры размера m×n. Тогда смешанная стратегия игрока Апредставляет собой вектор , удовлетворяющий условиям

,

а смешанная стратегия для игрока Бесть вектор 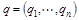, такой, что

.

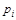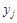Данное определение имеет следующий смысл: когда игрок А ис­пользует смешанную стратегию p, он применяет случайный способ вы­бора стратегии, при котором чистая стратегия выбирается с вероят­ностью , где . Аналогично игрок Б, используя смешанную стратегию q применяет случайный способ выбора стратегии, при кото­ром чистая стратегия выбирается с вероятностью , где 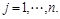Эти две схемы рандомизации будем предполагать независимыми, так что вероятность того, что в партии игрок А выберет стратегию , а игрок Б - 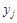, равна 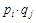. Так как платеж в этом случае равен , математи­ческое ожидание результата игры (средний платеж игрока А при розыг­рыше большого числа партий) выражается формулой

,

или в матричных обозначениях

,

где значок t означает транспонирование.

Для смешанных стратегий седловая точка определяется как пара стратегий удовлетворяющих условию

для любых стратегий , где P и Q - множества допустимых смешанных стратегий игроков А и Б, соответственно.

Теорема. Каждая матричная игра имеет, по крайней мере, одну седловую точку в смешанных стратегиях.

Эта теорема носит название теоремы о минимаксе. Из нее следует, что для любой матричной игры

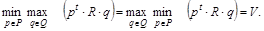
Величина V обычно называется ценой или значением игры.

Def. Оптимальной называется такая стратегия игрока, которая гарантирует ему (в смысле математического ожидания) выигрыш, равный цене игры.

Таким образом, стратегия оптимальна для игрока А, если

,

и стратегия оптимальна для игрока Б, если

.

Теорема о минимаксе гарантирует существование, по крайней ме­ре, одной оптимальной стратегии для каждого из игроков, т.е. матричные игры всегда имеют решение в смешанных стратегиях, и ниже мы рассмотрим алгоритмы его нахождения.

Дата добавления: 2015-06-04