Итерационный метод решения игр

Рассмотрим один из наиболее простых итерационных методов решения игр – метод Брауна - Робинсона. Основная идея метода заклю­чается в том, что игроки при многократном повторении игры при выборе стратегии в каждой конкретной партии используют весь накопленный в предыдущих партиях опыт.

Пусть 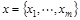- множество чистых стратегий игрока А, а - множество чистых стратегий игрока Б. Соответственно назо­вем эмпирическими смешанными стратегиями игроков А и Б после проведения k партий векторы

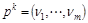и ,

где 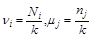- частота использования стратегий 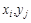в k пар­тиях, а 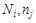- соответственно число использования стратегий 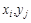в k партиях.

Алгоритм построения решения заключается в том, что разыгры­ва­ет­ся боль­шое число партий, причем в каждой партии каждый игрок вы­би­рает такую чистую стратегию, которая обеспечивает наилучший ре­зуль­тат для эмпи­ри­чес­кой смешанной стратегии, использованной против­ни­ком в предыдущихпар­тиях. После каждой партии значения 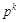и 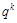пе­ре­считываются (так как изме­ня­ет­ся число сыгранных партий k). Выбор игроками стратегий в первой партии произволен, например, можно ис­пользовать минимаксные стратегии.

Доказано, что

и ,

где и - оптимальные стратегии игроков А и Б соответственно, а выиг­рыш игрока Б (проигрыш игрока А) стабилизируется и стремится к цене игры.

При практической реализации метода вычисления прекращаются, когда

,

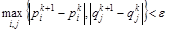где ε - заданная точность.

При использовании метода Брауна - Робинсона следует иметь в виду, что он сходится медленно, но прост в реализации на ЭВМ, причем уве­личение раз­мер­ности игры не приводит к ощутимому увеличению объ­ема вычислений, чего нельзя сказать о методе сведения к задачам линейного программирования.

Дата добавления: 2015-06-04