Распределение молекул газа по компонентам скорости

Распределение Больцмана

Барометрическая формула

Барометрическая формула. Распределение Больцмана

Для термодинамического равновесного состояния температура во всех частях системы одна и та же.

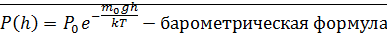
При соударении друг с другом или со стенками вакуумной камеры молекулы газа изменяют свои скорости, как по величине, так и по направлению. Тем не менее, в состоянии равновесия систему молекул можно описать с вероятностной точки зрения. Математически такое описание определяется заданием функции плотности вероятности распределения молекул по скоростям.

Рассмотрим объем идеального газа, находящийся при температуре T. Функция распределения молекул по скоростям определяется формулой Максвелла: 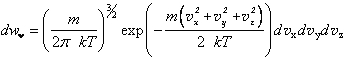, где υ x, υ y, υ z — декартовы компоненты скорости частицы, k — постоянная Больцмана, которая осуществляет связь между температурой и энергией, m — масса частицы.

Формула (1.11) определяет вероятность того, что молекула газа имеет скорость с декартовыми компонентами в интер-ах от υx до υx+dυx; от υy до υy+dυy; от υz до υz+υz.

Формула (1.11) может быть представлена в виде произведения трех независимых сомножителей, каждый из которых определяет распределение по соответствующей декартовой компоненте скорости, например, для компоненты x: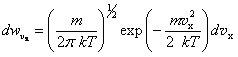

Интервалу абсолютных скоростей от υ до υ+dυ в пространстве скоростей υx, υy, υz соответствует сферический слой объемом 4πdυ2dυ. Тогда вероятность того, что скорость молекулы лежит в диапазоне от dυ до dυ+dυ, определяется формулой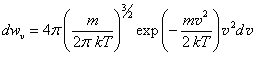

Формулу (1.13) можно также получить, сделав в (1.11) переход от декартовых координат к сферическим и выполнив интегрирование по углам. В заключение получим распределение молекул по энергии. Для этого заменим в формуле (1.13) mυ 2/2 на E, а dυ на 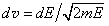соответственно: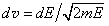

Формулы (1.12) и (1.14) удобно представить в инвариантном виде, вводя безразмерную энергию 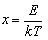и безразмерную скорость : 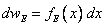, , 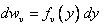где , .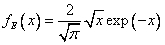

Максимум функции fυ(y) соответствует значению y=1, поэтому наиболее вероятная скорость равна 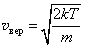. Среднюю скорость молекул можно найти, воспользовавшись формулой (1.9) с учетом (1.13). В результате вычисления интеграла получим 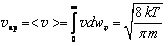, что в безразмерных единицах соответствует .

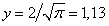Аналогично можно выразить среднеквадратичную скорость: , что в безразмерных единицах соответствует.

Для того чтобы найти среднюю энергию, воспользуемся распределением (1.14). В результате получим

Дата добавления: 2015-06-04