Плоская система произвольно расположенных сил 2 страница

Пример выполнения задания

Дано: схема фермы (рис. 16). Р₁=10 кН; Р₂= 20 кН; Р₃=10 кН; а=2 м.

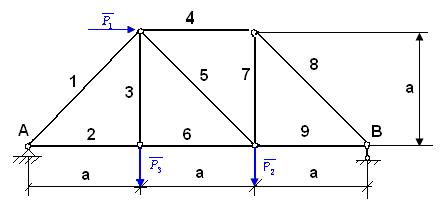
Рисунок 16

Решение:

1. Производим проверку условия геометрической неизменяемости и статической определимости фермы по формуле

S = 2n – 3,

где S – число стержней фермы;

n – число узлов фермы.

Подставляя S = 9 и n = 6, получаем, что

9 = 2 · 6 – 3 = 9 → 9 = 9

Это означает, что форма статически определяемая.

2. Определение реакций опор А и В (т. е. уравновесить ферму внешне) – рис. 17.

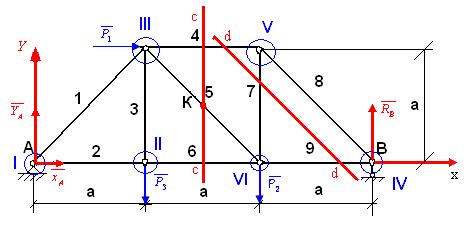
Рисунок 17

Освобождаем ферму от связей, заменяя их действие соответствующими силами реакции: 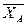, 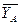- две составляющие реакции неподвижной шарнирной опоры А; 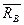- реакция опорного стержня В (направлена вдоль стержня) – рис. 17.

Заданные силы - 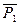, , 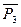(активные) и реакции опор - 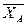, , 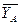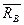(реактивные) образуют плоскую произвольную систему сил, для которой можно составить три уравнения равновесия:

1. ∑ F_kx = 0; X_A + P₁ = 0 → X_A = – P₁ = – 10 кН;

2. ∑ F_ky = 0; Y_A – P₃ – P₂ + R_B = 0

3. ∑ M_A (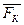) = 0; – aP₃ – aP₁ – 2aP₂ + 3aR_B = 0 =>

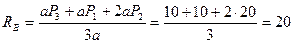кН.

Подставляем найденное значение реакцию 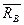в уравнение 2 и определяем реакцию Y_A:

Y_A = Р₃ + Р₂ – R_B = 10 + 20 – 20 = 10 кН

Проверка: точка К находится на середине вертикального и горизонтального размеров фермы.

∑ M_A (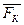) = 0; -15аY_A + 0,5aX_A – 0,5aP₁ – 0,5aP₂ + 0,5aP₃ + 1,5aR_B = 0; => –1,5 · 2 · 10 + 0,5·2 ∙(–10) – 0,5·2·10 +0,5·2·10 – 0,5·2·20 + 1,5·2·20 = 0 => –30 – 10 – 10 – 20 + 10 + 60 = 0; –70 + 70 = 0; 0 ≡ 0.

Знак «–» в значении реакции 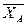указывает на то, что она направлена противоположно, чем показано на рис. 17, чтобы обеспечить равновесие полученной плоской произвольной системы сил.

Итак, Х_А = -10 кН; Y_A = 10 кН; R_B = 20 кН.

3. Определение усилий в стержнях фермы

а) способ вырезания узлов (аналитический).

Введем следующую нумерацию узлов и стержней фермы (узлы обозначены римскими, а стержни – арабскими цифрами) – рис. 17.

Вырезаем сначала узел I, в котором сходятся только 2 стержня с неизвестными усилиями. Усилия в стержне обозначим соответственно через 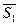, 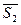…. . 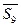Действия перерезанных стержней 1 и 2 заменим усилиям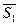и и 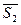, направленные от узла, предполагая, что все стержни растянуты – рис. 17. Силы, действующие на узел I, образуют плоскую систему сходящихся сил, поэтому можно составить уравнения равновесия.

Узел I.

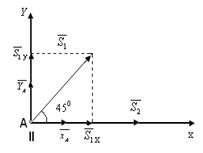∑ F_kx = 0; X_A + S₁cos45⁰ + S₂ =0 (1)

∑ F_ky = 0; Y_A + S₁cos 45⁰ = 0 (2)

Решая полученную систему уравнений, находим усилия в стержнях 1 и 2:

Рисунок 18

Из 2): S₁ = – y_A / sin45^o = – 10 / (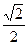) = – 14,14 кН (сжат)

Подставляем найденные значения S₁ в уравнение 1) и вычисляем S₂:

S₂ = – x_A – S₁ cos 45^o = – ( – 10) – ( – 14,14) 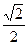^. () = 10 + 10 = 20 кН (растянут)

Положительный знак в значении S₂ показывает, что стержень 2, из выше принятого предположения, действительно растянут, а отрицательный знак в значении S₁ – что стержень сжат.

Следующим вырезаем узел II, в котором сходятся не более 2-х стержней (3 и 6) с неизвестными усилиями. Усилие S₂ направляем соответственно тому, что это внутреннее усилие в стержне (простейшая уравновешенная система сил).

Узел II:

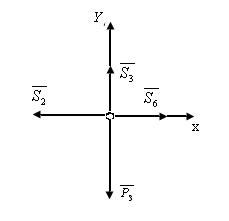∑Fkx = 0; S₆ – S₂ = 0 (1)

=> S₆ = S₂ = 20 кН (растянут).

∑Fky = 0; S₃ – P₃ = 0 (2)

=> S₃ = P₃ = 10 кН (растянут).

Рисунок 19

Аналогично вырезаем все остальные узлы.

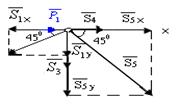Узел III:

∑Fkx = 0; -S₁ ^.cos 45^o + P₁ + S₄ + S₅ ^. cos 45^o = 0; (1)

Рисунок 20 ∑Fky = 0; -S₁ ^. sin45^o – S₃ – S₅ 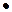^. sin45^o = 0 (2) => S₅ = 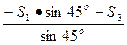= =0 => (нулевой стержень).

Подставляем S₅ в 1) и находим значение усилия S₄:

S_{4 =} S₁ cos 45^o – P₁ – S₅ cos 45^o = - 14,14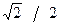^. () – 10 = - 10 - 10 = − 20 кН (сжат).

Узел IV:

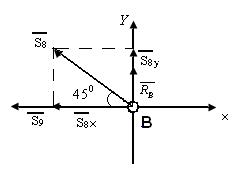∑Fkx = 0; − S₉ − S₈^.cos 45⁰ = 0 (1)

∑Fky = 0; R_в + S₈^.sin 45⁰ = 0 (2) =>

=> S_{8 =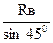} − = − = − 28,28 кН (сжат).

Рисунок 21

Из 1): S_{9 =} −S₈^.cos 45⁰ = − (−28,28)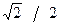^. () = 20 кН (растянут).

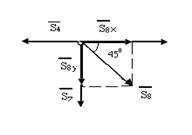Узел V:

∑Fkx = 0; −S₄ + S₈^.cos 45⁰ = 0 (1)

− (−20) – 28,28 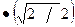=0; 20 – 20 = 0; 0 = 0

Рисунок 22

∑Fky = 0; –S₈^.sin 45⁰ – S₇ = 0

=> S₇ = –S₈^.sin 45⁰ = – (– 28,28) 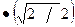= 20 кН (растянут).

Узел VI (проверочный):

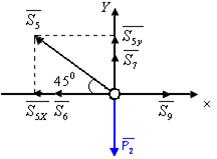∑Fkx = 0; –S₅ · cos 45⁰ – S₆ +S₉ = 0; (1)

–0 – 20 + 20 = 0; 0 ≡ 0

∑Fky = 0; S₅ · sin 45⁰ + S₇ – P₂ = 0; (2)

0 · (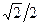) + 20 – 20 = 0; 0 ≡ 0;

Рисунок 23

б) способ Риттера (способ сечений) – определение усилий в стержнях 5, 6, 9.

Мысленно рассекаем ферму на две части так, чтобы число рассеченных стержней, в которых усилия еще не известны, не превышало трех.

Для стержней 5 и 6 сечение С-С (рис. 17). Рассматриваем равновесие левой от сечения С-С части фермы – рис. 24. Действие рассеченных стрежней 4, 5, 6 заменяем их внутренними усилиями S₄, S₅, S₆ соответственно, направленными по стержням от узлов, предполагая, что стержни растянуты. Для полученной плоской произвольной системы сил можно составить 3 уравнения равновесия. Точка Риттера – это моментная точка.

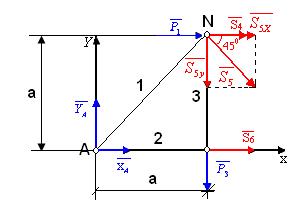Для стержня 6 точка N – точка Риттера – точка пересечения линий действия усилий S₄ и S₅.

∑M_N(F_K) = 0; a S₆ + aX_A – a Y_A = 0 => S₆ = = 10- (-10) = 20 кН (растянут).

Рисунок 24

Для стержня 5 точки Риттера нет.

∑Fky = 0; –S₅ sin45⁰ – P₃ + Y_A = 0; => S₅ = 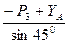= = 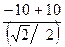0 (нулевой стержень)

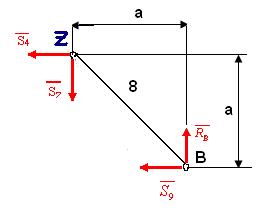Для определения внутреннего усилия в стержне 9 мысленно рассекаем ферму сечением d-d (рис. 17) и рассматриваем равновесие правой от сечения части фермы – рис. 25.

Точка Z – точка Риттера для стержня 9.

∑M_Z(F_K) = 0; –a S₉ + aR_B = 0 => S₉ = Рисунок 25 = 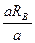= R_B = 20кН (растянут).

Численные значения внутренних усилий S_5, S₆, S₉ соответственно стержней 5, 6, 9,определенные по методу вырезания узлов фермы и способом сечений (метод Риттера) абсолютно равны. Схема фермы с фактической картиной сил

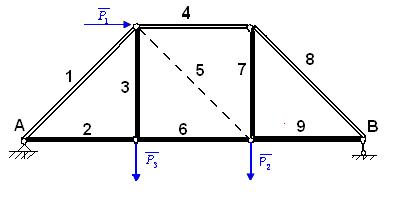сжатый стержень

растянутый стержень

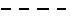стержень, сила которого равна нулю (нулевой стержень) Рисунок 26

Результаты расчетов внутренних усилий в стержнях фермы сводим в таблицу 4.

Таблица 4.

Номер стержня	1	2	3	4	5	6	7	8	9
Знак силы	–	+	+	–	0	+	+	–	+
Сила, кН	14,14	20	10	20	0	20	20	28,28	20

Ниже приводятся схемы расчётных заданий – рис. 27 – 33 (стр.36 – 42).

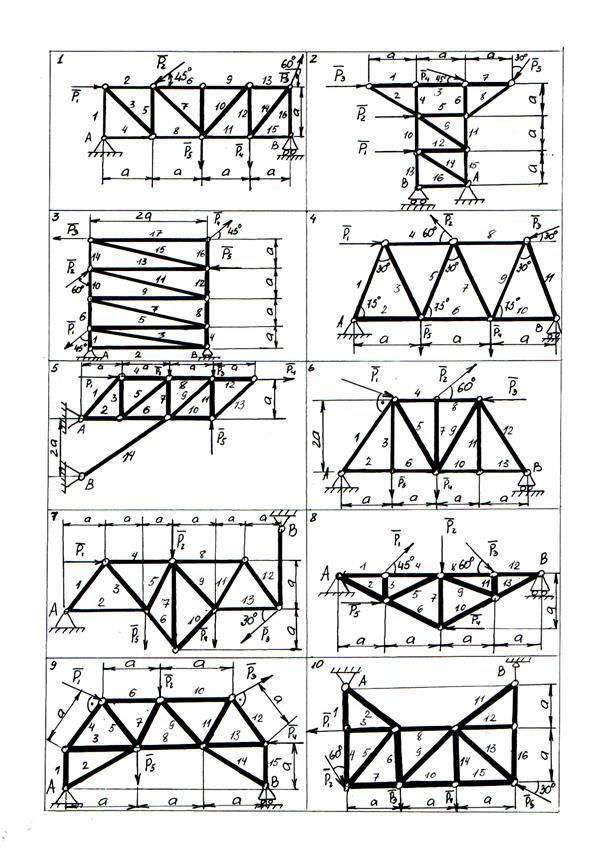
Рисунок 27

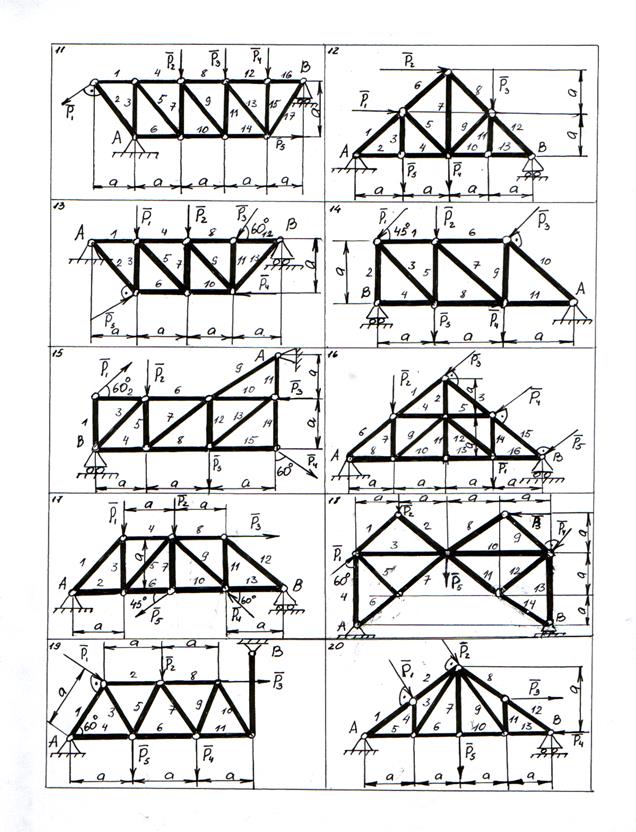
Рисунок 28

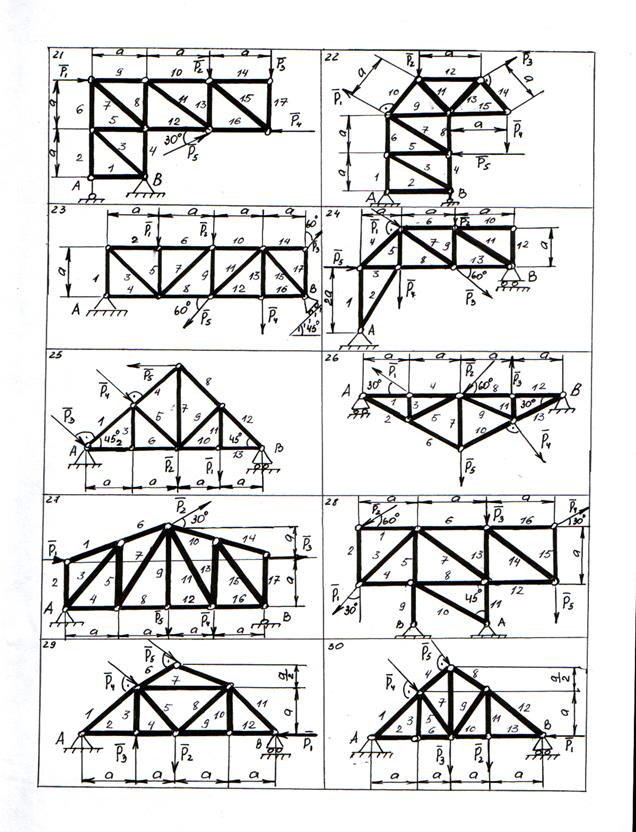
Рисунок 29

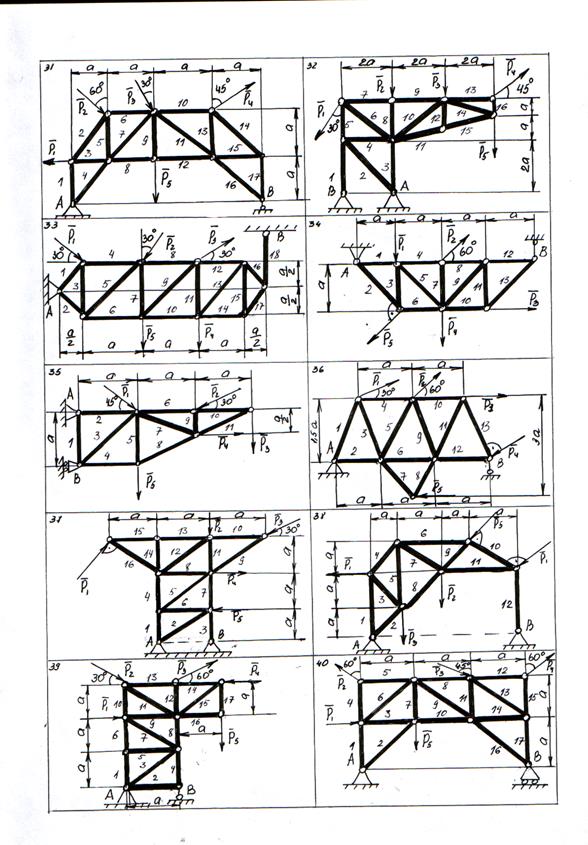
Рисунок 30

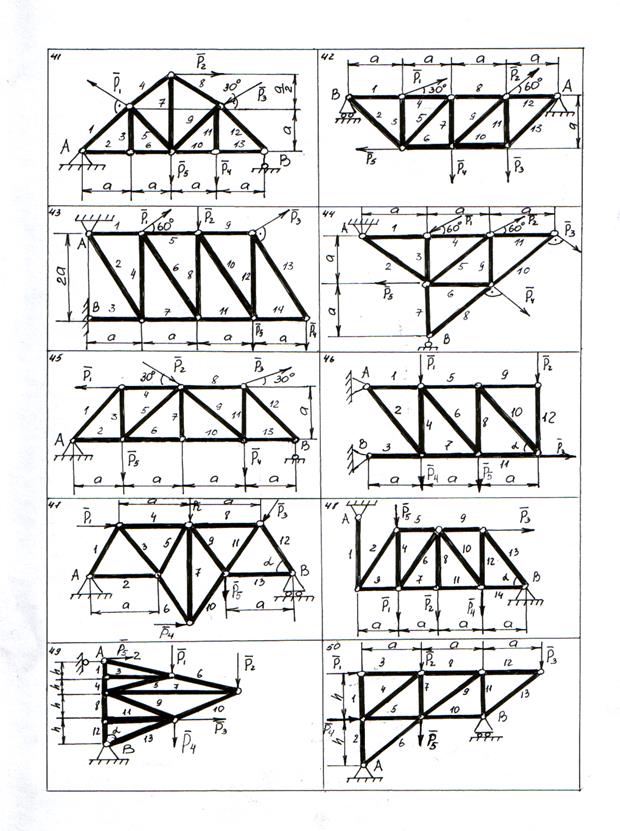
Рисунок 31

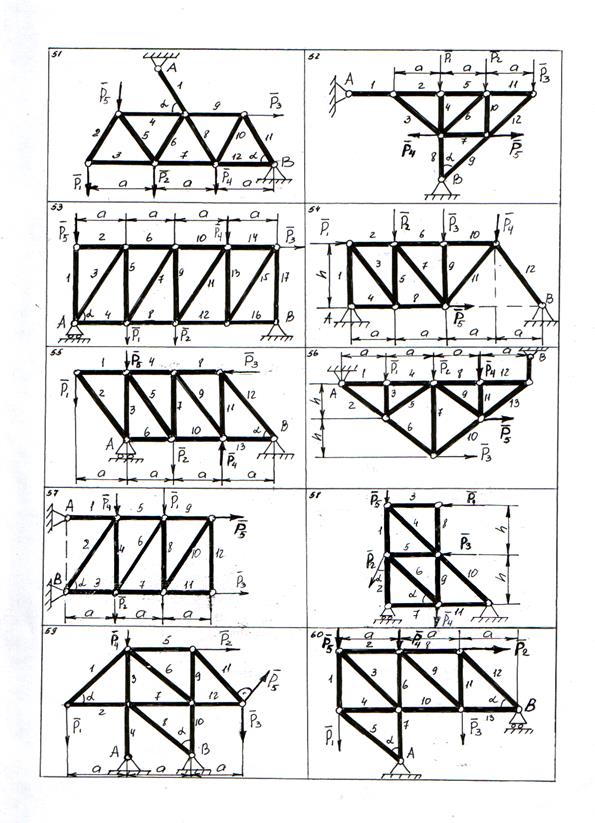
Рисунок 32

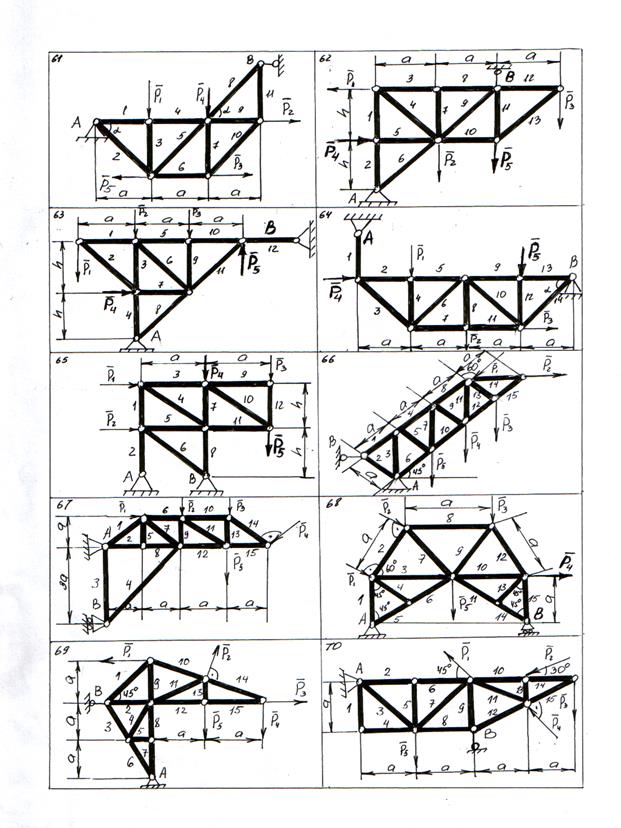
Рисунок 33

Вопросы для самопроверки:

1. Что такое ферма?

2. Где используются фермы?

3. Алгоритм расчета фермы?

4. Методы расчета ферм:

а) метод вырезания узлов;

б) метод Риттера.

5. Какая зависимость существует между числом стержней и числом узлов фермы?

6. Как определяется статическая определимость фермы?

7. Уравнения равновесия плоской системы: а) сходящихся сил? б) произвольной системы сил?

8. Определение и свойства простейшей уравновешенной системы сил?

9. Определение и свойства внутренних усилий?

Задание С – 3. Определение реакции опор составной конструкции

(система двух тел)

Конструкция состоит из двух частей, соединенных шарнирно. С – промежуточный шарнир конструкции. Прямые и изогнутые балки определяют геометрический контур конструкции. Размеры указаны на рис. 38 - 47 (№ 1 – 60) – с. 50 - 59. На конструкцию действуют: сосредоточенные силы 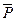_{1, 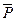2} ; равномерно - распределенная нагрузка интенсивностью 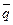; пара сил с моментом М. Исходные данные для расчетов приведены в таблице.5. Весом балок пренебречь.

Определить реакции опор конструкции и реакции промежуточного шарнира С.

Таблица 5.

№ варианта	Р1, кН	Р2, кН	М, кН ∙ м	q, кН/ м
1	2	3	4	5
1	5	-	24,0	0,8
2	6,0	10,0	22,0	1,0
3	7,0	9,0	20,0	1,2
4	8,0	-	18,0	1,4
5	9,0	-	16,0	1,6
6	10,0	8,0	25,0	1,8
7	11,0	7,0	20,0	2,0
8	12,0	6,0	15,0	2,2
9	13,0	-	10,0	2,4`
10	14,0	-	12,0	2,6
11	15,0	5,0	14,0	2,8
12	12,0	4,0	16,0	3,0
13	9,0	6,0	18,0	3,2
14	6,0	-	20,0	3,4
15	5,0	8,0	22,0	3,6
16	7,0	10,0	14,0	3,8
17	9,0	12,0	26,0	4,0
18	11,0	10,0	18,0	3,5
19	13,0	9,0	30,0	3,0
20	15,0	8,0	25,0	2,5
21	10,0	7,00	20,0	2,0
22	5,0	6,0	15,0	1,5
23	8,0	5,0	10,0	1,4
24	11,0	4,0	5,0	1,3
25	14,0	6,0	7,0	1,2
26	12,0	8,0	9,0	1,1
27	10,0	7,0	11,0	1,0
28	8,0	9,0	13,0	1,2
29	6,0	10,0	15,0	1,4
30	10,0	12,0	17,0	1,6
31	15,0	14,0	10,0	3
32	13,0	12,0	6,0	2
33	11,0	10,0	5,0	1,0
34	9,0	8,0	14,0	3,0
35	7,0	6,0	12,0	2,0
36	8,0	5,0	4,0	1,0
37	7,0	4,0	10,0	2,0
38	6,0	6,0	7,0	1,0
39	5,0	8,0	8,0	3,0
40	4,0	10,0	6,0	2,0
41	12,0	11,0	12,0	1,0
42	10,0	6,0	10,0	2,0
43	9,0	5,0	6,0	1,0
44	7,0	10,0	13,0	2,0
45	6,0	8,0	5,0	1,0
46	3,0	10,0	10,0	2,0
47	1,0	8,0	8,0	1,0
48	3,0	6,0	6,0	3,0
49	5,0	4,0	7,0	2,0
50	7,0	2,0	5,0	1,0
51	10,0	9,0	4,0	2,0
52	8,0	7,0	7,0	1,0
53	6,0	5,0	8,0	2,0
54	4,0	3,0	3,0	1,0
55	2,0	1,0	2,0	2,0
56	7,0	1,0	7,0	2,0
57	6,0	2,0	5,0	1,0
58	5,0	3,0	10,0	2,0
59	4,0	4,0	5,0	1,0
60	3,0	5,0	10,0	2,0

Пример выполнения задания: На конструкцию (рис. 34), состоящую из балок АС и СВ действует сосредоточенная сила 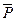₁, равномерно – распределённая нагрузка интенсивностью 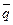;, пара сил с моментом М.

Дано: Р₁ = 2 кН; q = 2 кН/м; М = 6 кН∙м; α = 60⁰; Определить реакции опор А и В и реакции промежуточного шарнира С.

Рисунок 34

Решение: 1- й способ: Рассмотрим равновесие всей конструкции (рис. 35) Равномерно – распределённую нагрузку интенсивностью q заменяем равнодействующей 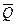, численно равной Q = 6 ∙q = 6 ∙ 2 = 12 [м ∙ (кН/м)] = кН и приложенной в центре тяжести прямоугольника – на пересечении диагоналей. Вводим систему отчёта ХАУ.

Сосредоточенную силу 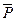₁ разлагаем по правилу параллелограмма на две составляющие по осям Х и У – 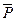_1хи 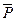_1у, численно равные:

P_1х = P₁ ∙ cos60⁰ =2 ∙ (½) = 1 кН

P_1у = P₁ ∙ sin60⁰ = 2 ∙ (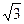 / 2) = 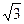= 1,73 кН.

Применяя принцип освобождаемости от связей отбрасываем опору А (жесткая заделка) и опору В (невесомый стержень) и заменяем их реакциями опор (рис. №2). Реакции опоры 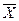А – _А, 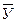_А, Ма; реакция опоры В – 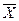_В (направлена вдоль стержня). Рассмотрим систему уравновешивающихся сил, приложенных к конструкции.

Для полученной плоской произвольной системы сил (рис. 35) можно составить три уравнения равновесия:

∑ F_кх = 0; X_в + X_а – P_1х = 0; (1)

∑ F_ку = 0; Y_а – Q – P_1у = 0; (2) => Y_а = Q + P_1у = 12 + 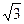= 13,73 kH;

∑ Mа (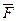 _к) = 0; Ma +М – 5Q – 8P_1у + 2P_1х = 0; (3)

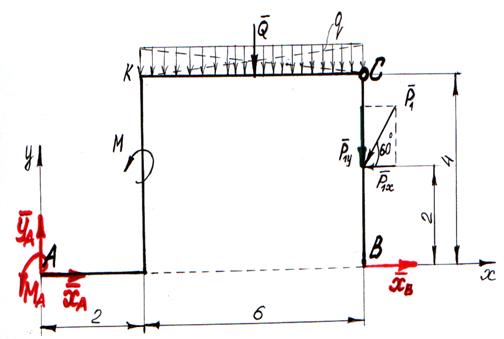
Рисунок 35

Из 3) => Ma = – M + 5Q + 8P_1у – 2P_1х = – 6 + 5 ∙ 12 + 8 ∙ 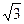– 2 ∙ 1 = 65,84 kH ∙ м.

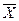Расчленяем конструкцию на две составные части в точке подвижного соединения – шарнир С – и рассматриваем равновесие правой от шарнира С части конструкции (рис. 36). Реакцию шарнира С разлагаем на две составляющие – _с, 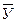_с. Эти реактивные силы отражают действие отброшенной левой части конструкции на рассматриваемую правую. Для полученной плоской произвольной системы сил (рис. 36) можно составить 3 уравнения равновесия:

∑ Fkx = 0; X_в + X_с – P_1х = 0; (4)

∑ Fky = 0; Y_с – P_1у = 0; => Y_с = P_1у = 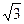kH; (5)

∑ Mc (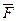 _к) = 0; – 2P_1х + 4X_в = 0 (6) =>

=> X_в = (2P_1х ) / 4 = P_1х / 2 = 1/2 = 0,5 kH;

Рисунок 36

Зная Хв из уравнения 4) находим Хс: Хс = Р_1х – Хв = 1 – 0,5 = 0,5 kH;

Подставляем найденную Хв в уравнение 1) и определяем Ха: Ха = Р_1х – Хв = 1 – 0,5 = 0,5 kH;

Выполним проверку правильности вычисления реакций опор.

∑ Мк (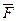 _к) = 0; – (рис. 35)

–2Уа + Ма + 4Ха + М – 3Q – 6P_1у – 2P_1х + 4Xв = 0

–2 ∙ 13, 73 + 65,84 + 4 ∙ 0,5 + 6 – 3 ∙ 12 – 6 ∙ 1,73 – 2 ∙ 1 + 4 ∙ 05 = 0

–27,46 + 65,84 + 2 + 6 –36 – 10,38 – 2 + 2 = 0

–73,84 + 73,84 = 0; 0 ≡ 0

Второй способ решения: Расчленяем конструкцию на две составные части в точке подвижного соединения – шарнир С – и рассматриваем равновесие каждой (левой и правой) части конструкции отдельно. Рассмотрим равновесие левой от шарнира С – АС – части конструкции - (рис. 37). Реакцию шарнира С (действие отброшенной правой части на левую) разлагаем на две составляющие 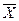'_с, 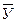'_с. Причём 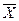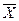'_с = – _с, 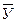'_с = – 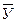_с. Для полученной плоской произвольной системы сил можно составить три уравнения равновесия:

Дата добавления: 2015-06-04