
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пространственная система произвольно расположенных сил. 2 страница
|
|
|
|
Из уравнения 6/),подставляя найденное значение  ,определяем величину реакции
,определяем величину реакции 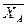 :
:
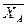 =
= 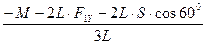 =
= 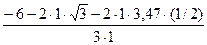 = – 4,31 кН;
= – 4,31 кН;
Зная  и
и 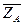 ,из уравнения 3/) определяем величину реакции
,из уравнения 3/) определяем величину реакции 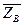 :
:
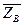 = – ZA+P – F2+F1Z – S·sin600 = – 0,5+8– 4+1– 3,47·(
= – ZA+P – F2+F1Z – S·sin600 = – 0,5+8– 4+1– 3,47·( /2) = 1,49 кН;
/2) = 1,49 кН;
Из уравнения 2/), зная  , вычисляем значение реакции
, вычисляем значение реакции  :
:
 = F1Y+S·cos600 =
= F1Y+S·cos600 =  +3,47·
+3,47· 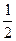 = 3,47 кН:
= 3,47 кН:
Зная 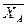 , из уравнения 1/)
, из уравнения 1/) 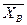 = –
= – 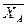 = – (– 4,31) = 4,31 кН;
= – (– 4,31) = 4,31 кН;
Проверка:
∑FAX=0; XA+XB=0;
4,31 – 4,31=0;
0 ≡ 0;
∑FAY=0; YA – F1Y – S·cos600=0;
3,47–  – 3,47·
– 3,47· 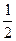 =0;
=0;
3,47– 3,47=0;
0 ≡ 0,
∑FAZ=0; ZA+ZB – P+F2 – F1Z+S·sin600=0;
0,5+1,49 – 8+4 – 1+3,47·( /2)=0;
/2)=0;
0 ≡ 0 
Результаты расчётов сводим в таблицу 12.
Таблица 12.
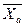 , кН , кН
| 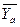 , кН , кН
| 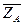 , кН , кН
| 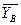 , кН , кН
| 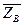 , кН , кН
|  , кН , кН
|
| - 4,31 | 3,47 | 0,5 | 4,53 | 1,49 | 3,47 |
Пример 2 (к вариантам 11-20):
Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром в точке А, цилиндрическим шарниром (подшипником) в точке В и невесомым стержнем 1 (рис.1).
Вес большой плиты Р1 = 5 кН; вес меньшей плиты Р2 = 3 кН. На плиты действует пара сил (параллельная плоскости XY) с моментом М = 4 кН·м; сила  (
(
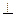 AY) и ее составляющие F2X = F2·sin600; F2Z = F2·cos600; F2 = 8 кН; а = 0,6 м; F1 = 6 кН (
AY) и ее составляющие F2X = F2·sin600; F2Z = F2·cos600; F2 = 8 кН; а = 0,6 м; F1 = 6 кН ( 1//AY): Определить реакции опор А и В и стержня 1.
1//AY): Определить реакции опор А и В и стержня 1.
Решение:
1. Рассмотрим равновесие плит. На плиты действуют заданные силы 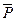 1 и
1 и 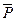 2, пара с моментом М,
2, пара с моментом М, 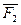 и ее составляющие F2X = F2sin600 = 8·
и ее составляющие F2X = F2sin600 = 8· 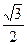 = 6,93 кН; F2Z = F2cos600 = 8·
= 6,93 кН; F2Z = F2cos600 = 8· 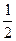 = 4 кН; и реакции связей: реакцию сферического шарнира А разложим на три составляющие
= 4 кН; и реакции связей: реакцию сферического шарнира А разложим на три составляющие 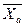 ,
, 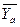 ,
, 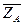 ; цилиндрического подшипника В – на две составляющие
; цилиндрического подшипника В – на две составляющие 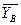 и
и 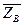 (в плоскости,перпендикулярной оси подшипника), реакцию
(в плоскости,перпендикулярной оси подшипника), реакцию  стержня направляем вдоль стержня (рис.2).
стержня направляем вдоль стержня (рис.2).

1.
2.
3.
4.
Для полученной пространственной произвольной системы сил можно составить шесть уравнений равновесия:
∑FAX=0; XA+F2X = 0 => 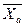 = – F2X = – 6,93 кН; (1)
= – F2X = – 6,93 кН; (1)
∑FAY=0; YB+YA+F1=0; (2)
∑FAZ=0; ZA – P2+ZB – P1+F2Z+S=0; (3)
∑МАХ(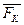 )=0; – 3аF1+4a·F2Z+4a·S – 2a·P1=0; (4)
)=0; – 3аF1+4a·F2Z+4a·S – 2a·P1=0; (4)
∑МAY(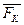 )=0; – 2a·ZA+a·P2 – a·P1+3a·F2X – a·F2Z=0; (5)
)=0; – 2a·ZA+a·P2 – a·P1+3a·F2X – a·F2Z=0; (5)
∑МAZ(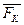 )=0; 2a·YB+2a·F1+M – 4a·F2X=0; (6)
)=0; 2a·YB+2a·F1+M – 4a·F2X=0; (6)
Из (6) находим 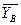 :
:
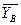 =
= 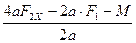 =
= 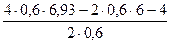 =
= 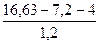 = 4,53 кН;
= 4,53 кН;
Из (5) находим  :
:
 =
= 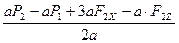 =
= 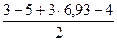 = 7,39 кН;
= 7,39 кН;
Из (4) находим  :
:
 =
= 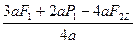 =
= 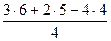 =
= 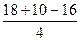 = 3 кН;
= 3 кН;
Из (3) находим 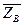 :
:
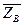 = – ZA+P2+P1 – F2Z – S = – 7,39+3+5 – 4– 3 = – 6,39 кН;
= – ZA+P2+P1 – F2Z – S = – 7,39+3+5 – 4– 3 = – 6,39 кН;
Из (2) находим 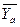 :
:
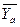 = – YB – F1 = – 4,53 – 6 = – 10,53 кН;
= – YB – F1 = – 4,53 – 6 = – 10,53 кН;
Результаты расчётов сводим в таблицу 13:
Таблица 13.
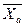 , кН , кН
| 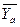 , кН , кН
| 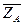 , кН , кН
| 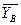 , кН , кН
| 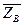 , кН , кН
|  , кН , кН
|
| - 6,93 | - 10,53 | 7,39 | 4,53 | - 6,39 | 3 |
Пример 3 (к вариантам 21 – 35)
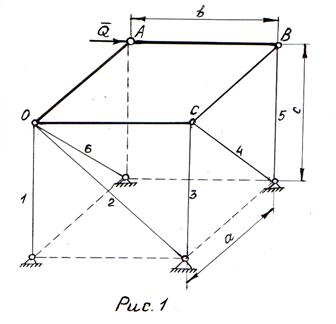
Однородная прямоугольная пластина АОВС весом 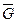 удерживается в горизонтальной плоскости, опираясь на стержневой параллелепипед. Стержни соединены друг с другом шарнирно. В узле А приложена сила
удерживается в горизонтальной плоскости, опираясь на стержневой параллелепипед. Стержни соединены друг с другом шарнирно. В узле А приложена сила 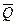 . Размеры параллелепипеда указаны на рисунке. (рис. 1)
. Размеры параллелепипеда указаны на рисунке. (рис. 1)
Дано: 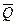 = 20 кН;
= 20 кН; 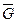 = 18 кН; а = 400 см; в = 400 см; с = 450 см.
= 18 кН; а = 400 см; в = 400 см; с = 450 см.
Определить усилия в стержнях, обозначенных на рис.1 – 1, 2, 3, 4, 5, 6.
Решение:
1. Рассмотрим равновесие конструкции, состоящей из однородной прямоугольной пластины, закреплённой на стержневом параллелепипеде. В узле А приложена сила 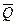 . Вес пластины
. Вес пластины 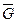 приложен в центре тяжести пластины (на пересечении диагоналей). Усилия в стержнях 1, 2, 3, 4, 5, 6 обозначаем соответственно
приложен в центре тяжести пластины (на пересечении диагоналей). Усилия в стержнях 1, 2, 3, 4, 5, 6 обозначаем соответственно  1,
1,  2,
2,  3,
3,  4,
4,  5,
5,  6, направляя их по стержням от узла, предполагая, что стержни растянуты. Вводим систему отсчёта ХОУZ.
6, направляя их по стержням от узла, предполагая, что стержни растянуты. Вводим систему отсчёта ХОУZ. 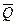 ||
|| 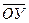 ;
; 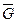 ||
|| 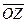 – (рис. 2).
– (рис. 2).
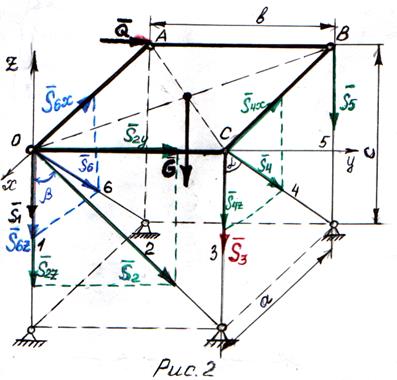
2. Для полученной пространственной произвольной системы сил можно составить шесть уравнений равновесия для определения шести неизвестных реакций опор – усилий в стержнях -  1,
1,  2,
2,  3,
3,  4,
4,  5,
5,  6. Конструкция статически определима.
6. Конструкция статически определима.
Вычислим направляющие косинусы наклонных стержней параллелепипеда – cos α, cos β, sin α, sin β. Так как а = в, то
cos α = cos β = 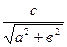 =
= 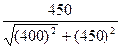 = 0, 7474
= 0, 7474
sin α = sin β = 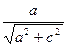 =
= 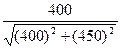 = 0,6644
= 0,6644
Σ Fох = 0; – S4 ·sin α – S6 ·sin α = 0; (1)
Σ Fоу = 0; S2· sin β + Q = 0; (2)
Σ Fоz= 0; – S1 – S2 · cos β – S4· cos α – S5 – S6 ·cos α – G = 0; (3)
Σ Мох ( к) = 0; – S3 · b – S4 · cos α ·b – S5· b – G · (1/2b) = 0; (4)
к) = 0; – S3 · b – S4 · cos α ·b – S5· b – G · (1/2b) = 0; (4)
Σ Моу ( к) = 0; – S5 · а – G · (1/2а) = 0; (5)
к) = 0; – S5 · а – G · (1/2а) = 0; (5)
Σ Моz( к) = 0; S4 · sin α · b – Q ·а = 0. (6)
к) = 0; S4 · sin α · b – Q ·а = 0. (6)
Из уравнения 6) находим численное значение  4:
4:
 4 =
4 = 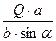 =
= 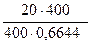 = 30, 10 кН;
= 30, 10 кН;
Из уравнения 5) определяем величину реакции стержня 5 –  5:
5:
 5 = –
5 = – 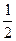 G = –
G = – 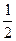 · 18 = – 9 кН;
· 18 = – 9 кН;
Из уравнения 2) находим численное значение усилия стержня
2 –  2 :
2 :
 2 =
2 =  =
= 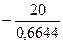 = – 30,10 кН;
= – 30,10 кН;
Из уравнения 1) определяем величину реакции стержня 6 –  6 :
6 :
 6 = – S4 = 30, 10 кН;
6 = – S4 = 30, 10 кН;
Из уравнения 4) находим численное значение усилия стержня 3 –  3 :
3 :
 3 = – S4 · cos α – S5 –
3 = – S4 · cos α – S5 – 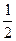 G = – 30,10 ∙ 0,7474 + 9 –
G = – 30,10 ∙ 0,7474 + 9 – 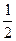 ∙ 18 = – 22,498 кН;
∙ 18 = – 22,498 кН;
Из уравнения 3) определяем величину реакции стержня 1 –  1 :
1 :
 1 = – S2 · cos β – S3 – S4 · cos α – S5 – S6 ·cos α – G = – 30,10 · 0,7474 + 22,498 – 30,10 · 0,7474 + 9 + 30,10 · 0,7474 – 18 = 36 кН.
1 = – S2 · cos β – S3 – S4 · cos α – S5 – S6 ·cos α – G = – 30,10 · 0,7474 + 22,498 – 30,10 · 0,7474 + 9 + 30,10 · 0,7474 – 18 = 36 кН.
Знак «– «в значениях реакций  5,
5,  2,
2,  6 ,
6 ,  3 указывает на то, что истинное направление этих реактивных сил соответствует противоположному, чем показано на рис. 2, чтобы обеспечить равновесие конструкции.
3 указывает на то, что истинное направление этих реактивных сил соответствует противоположному, чем показано на рис. 2, чтобы обеспечить равновесие конструкции.
Результаты расчётов сводим в таблицу 14:
Таблица 14
 1, кН 1, кН
|  2 , кН 2 , кН
|  3, кН 3, кН
|  4, кН 4, кН
|  5, кН 5, кН
|  6, кН 6, кН
|
| 36 | – 30,10 | – 22,498 | 30, 10 | –9 | –30, 10 |
Пример 4 (к схемам №36 – 40)
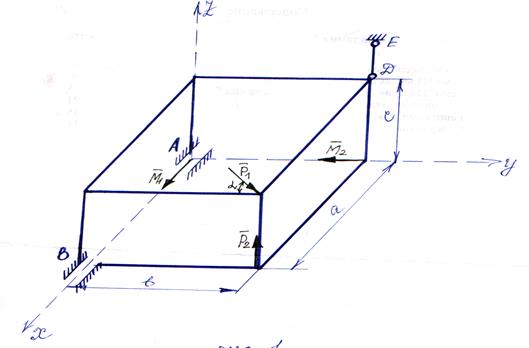
Рис. 1
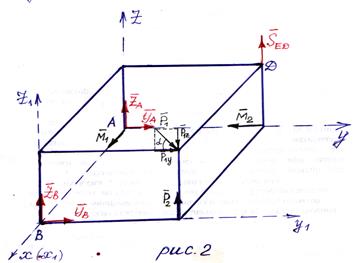
Однородное тело под действием наложенных на него связей и приложенных к нему сил находится в равновесии. (рис. 1)
Пренебрегая трением в местах сочленений определить опорные реакции в точках А и В, а также усилия стержня ЕD, поддерживающего тело. Вес стержня не учитывать.
Дано: Р1= 200 Н; Р2 = 400; М1 = 200 Н ∙м; М2 =400 Н∙м; 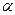 = 45◦; а = 0,8 м; в = 0,6м; с = 0,4м
= 45◦; а = 0,8 м; в = 0,6м; с = 0,4м
Решение:
1. Выполним рис. 2, на котором изображаем все активные (заданные по условию задачи) и реактивные (реакции опор) силы. На тело действуют: сосредоточенная сила 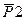 (
(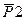 // АZ); сосредоточенная сила
// АZ); сосредоточенная сила 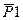
(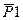 // YZ) и её составляющие
// YZ) и её составляющие 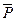 1у = Р1 cos 45◦ = 200 ∙
1у = Р1 cos 45◦ = 200 ∙ 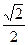 = 141 Н; Р1z = P1 ∙ sin 45◦ = 200 ∙
= 141 Н; Р1z = P1 ∙ sin 45◦ = 200 ∙ 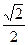 = 141 Н; пара сил с моментом М1 (М1 //АX) и М2 (М2//АY)
= 141 Н; пара сил с моментом М1 (М1 //АX) и М2 (М2//АY)
По принципу освобождаемости от связей мысленно отбрасываем опоры, заменяя их реакциями связей (опор): реакции цилиндрических шарниров (подшипников) А и В разлагаем на две составляющие
(перпендикулярные оси подшипника) – 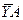 ,
, 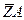 и
и 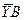 ,
, 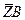 соответственно. Предполагаем, что стержень ED растянут и направляем усилие
соответственно. Предполагаем, что стержень ED растянут и направляем усилие  вдоль стержня от D к E. (рис. 2)
вдоль стержня от D к E. (рис. 2)
1. Для полученной пространственной произвольной системы сил для определения пяти неизвестных реакций опор –  ,
,  и
и  ,
, 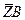 ,
,  можно составить шесть уравнений равновесия:
можно составить шесть уравнений равновесия:
1-й способ решения:
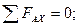 (1) – уравнение не имеет смысла для данной системы сил
(1) – уравнение не имеет смысла для данной системы сил
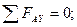
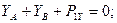 (2)
(2)
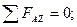
 (3)
(3)
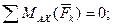 М1 + b∙SЕД – с∙Р1у – b∙Р1z + b∙Р2 = 0; (4)
М1 + b∙SЕД – с∙Р1у – b∙Р1z + b∙Р2 = 0; (4)
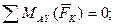 – М2 + а∙ Р1z – а∙Р2 – а∙ZВ = 0; (5)
– М2 + а∙ Р1z – а∙Р2 – а∙ZВ = 0; (5)
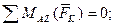 а∙Р1у + а∙УВ = 0 (6)
а∙Р1у + а∙УВ = 0 (6)
Изуравнения 6) вычисляем реакцию 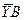 :
:
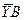 = –
= – 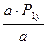 = – Р1у = – 141 Н;
= – Р1у = – 141 Н;
Подставляем найденную 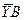 в уравнение 2) и определяем численное значение реакции
в уравнение 2) и определяем численное значение реакции 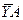 :
: 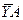 = –Y
= –Y 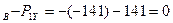
Из уравнение 4) вычисляем реакцию 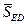 стержня ЕD:
стержня ЕD:
 =
= 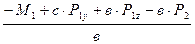 =
= 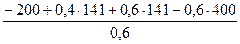 =
=
= – 498,33 Н;
Из уравнения 5) определяем численную величину реакции  :
:
 =
= 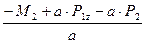 =
= 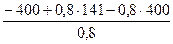 = – 759 Н
= – 759 Н
Подставляем найденные 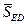 и
и 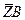 в уравнение 3) и вычисляем
в уравнение 3) и вычисляем 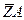 :
:
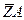 = –SЕД + Р1z – ZВ = – (– 498,33) + 141 – (–759) = 1398,33 Н
= –SЕД + Р1z – ZВ = – (– 498,33) + 141 – (–759) = 1398,33 Н
Проверка:
∑ FВУ1 = 0; 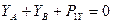
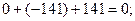
0≡0;
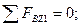 ZА + SЕД – Р1z + ZВ = 0
ZА + SЕД – Р1z + ZВ = 0
1398,33 – 498,33 – 141 –759 = 0
1398,33 – 1398,33 = 0
0≡0;
2-й способ решения:
Вводим систему отсчёта BX  Y
Y  Z
Z  с центром пересечения осей – В.
с центром пересечения осей – В.
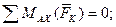 М1 + b ∙ SЕД – с ∙ Р1у – b ∙ Р1z + b ∙ Р2 = 0; (1َ)
М1 + b ∙ SЕД – с ∙ Р1у – b ∙ Р1z + b ∙ Р2 = 0; (1َ)
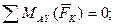 – М2 + а∙ Р1z – а ∙ Р2 – а ∙ ZВ = 0; (2َ)
– М2 + а∙ Р1z – а ∙ Р2 – а ∙ ZВ = 0; (2َ)
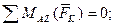 а∙Р1у + а∙УВ = 0 (3َ)
а∙Р1у + а∙УВ = 0 (3َ)
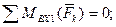 М1 + b ∙ SЕД + b ∙ Р2 – с ∙ Р1у – b ∙ Р1z = 0; (4َ)
М1 + b ∙ SЕД + b ∙ Р2 – с ∙ Р1у – b ∙ Р1z = 0; (4َ)
 а∙ZА – М2 + а ∙ SЕД = 0; (5َ)
а∙ZА – М2 + а ∙ SЕД = 0; (5َ)
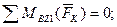 – а ∙ УА = 0 (6َ)
– а ∙ УА = 0 (6َ)
Из уравнения 6َ) Y 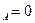 ;
;
Из уравнения 1َ) находим численное значение реакции стержня ED -  :
:
 =
= 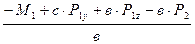 =
= 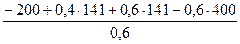 = – 498,33 Н;
= – 498,33 Н;
Уравнения 1َ) и 4َ) дублируют друг друга
Из уравнения 2َ) определяем численную величину реакции 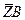 :
:
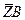 =
= 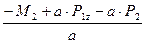 =
= 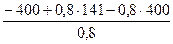 = – 759 Н;
= – 759 Н;
Из уравнения 3َ) вычисляем реакцию 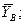
УВ =  = – Р1у = – 141 Н;
= – Р1у = – 141 Н;
Подставляем найденную  в уравнение 5َ) находим реакцию
в уравнение 5َ) находим реакцию 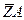 :
:
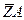 =
= 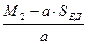 =
= 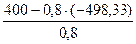 = 1398,33 Н
= 1398,33 Н
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2545; Нарушение авторских прав?; Мы поможем в написании вашей работы!