
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пространственная система произвольно расположенных сил. 3 страница
|
|
|
|
Проверка:
∑ FАУ = 0; 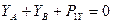
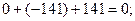
0≡0;
∑ FАZ = 0; ZА + SЕД – Р1z + ZВ = 0
1398,33 – 498,33 – 141 – 759 = 0
1398,33 – 1398,33 = 0
0≡0;
Результаты расчётов сводим в таблицу 15:
Таблица 15.
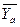 , кН , кН
| 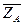 , кН , кН
| 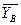 , кН , кН
| 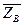 , кН , кН
|  ЕД, кН ЕД, кН
|
| 0 | 1398,33 | – 141 | – 759 | – 498,33 |
 Пример 5 (к вариантам 41-60)
Пример 5 (к вариантам 41-60)
Ступенчатый вал (рис.1) закреплен двумя цилиндрическими шарнирами (подшипниками) – опора А и В. Диск радиуса R и два стержня длиной а жестко закреплены к валу. На конструкцию действуют: сосредоточенная сила 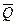 (
(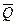 //AX); сосредоточенная сила
//AX); сосредоточенная сила 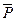 2 (
2 (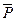 2 //АZ); сосредоточенная сила
2 //АZ); сосредоточенная сила 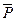 1 под углом α к оси АХ (
1 под углом α к оси АХ (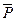 1
1 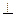 AY); пара сил с
AY); пара сил с
моментом М, лежащая в плоскости ХY (в плоскости вала),
Дано: P1 = 4 кН; Р2 = 8 кН; М = 6 кН·м; а = 4м; в = 6м; с = 2м; R = 2м; α =600
Определить реакции опор А, В, силу Q из условий равновесия конструкции.
Решение:

Рассмотрим равновесие конструкции. На нее действуют: заданные силы – сосредоточенная сила 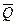 ||АХ; сосредоточенная сила
||АХ; сосредоточенная сила 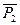 || AZ; сосредоточенная сила
|| AZ; сосредоточенная сила 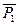 под углом α к оси АХ (разлагаем её на две составляющие
под углом α к оси АХ (разлагаем её на две составляющие 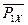 и
и 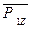 , учитывая, что
, учитывая, что 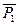
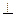 АY)
АY)
P1Х = Р1·cos α = 4· 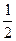 = 2 кН;
= 2 кН;
Р1Z = Р1·sin α = 4· 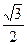 = 3,46 кН;
= 3,46 кН;
Пара сил с моментом М, лежащая в плоскости вала (ху) и реактивные силы (реакции опор) – реакцию цилиндрического шарнира (подшипника) разложим на две составляющие - 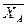 ,
, 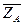 и
и 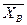 ,
, 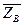 соответственно (в плоскости, перпендикулярной оси подшипника) – рис. 2.
соответственно (в плоскости, перпендикулярной оси подшипника) – рис. 2.
Для определения пяти неизвестных 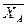 ,
, 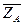 ,
, 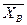 ,
, 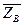 и
и 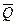 для полученной пространственной произвольной системы сил можно составить шесть уравнений равновесия:
для полученной пространственной произвольной системы сил можно составить шесть уравнений равновесия:
Первый способ решения:
∑ FAX = 0; –Q +XA – P1X + XB = 0; (1)
∑ FAY = 0; (2) – уравнение не имеет смысла для данной системы сил;
∑ FAZ = 0; ZA – P1Z + P2 + ZB = 0; (3)
∑ MAX (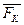 ) = 0; – a· P1Z + (a + b)· P2 + (a + b + c) · ZB = 0; (4)
) = 0; – a· P1Z + (a + b)· P2 + (a + b + c) · ZB = 0; (4)
∑ MAY (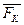 ) = 0; –R·Q + a· P1Z + a· P2 = 0; (5)
) = 0; –R·Q + a· P1Z + a· P2 = 0; (5)
∑ MAZ (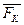 ) = 0; –a·Q + a· P1X + M – (a + b + c)· XB = 0 (6)
) = 0; –a·Q + a· P1X + M – (a + b + c)· XB = 0 (6)
При вычислении моментов относительно осей АХ и АZ силы 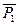 применяем теорему Вариньона:
применяем теорему Вариньона:
MAX (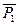 ) = MAX (
) = MAX (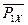 ) + MAX (
) + MAX (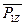 );
);
MAZ (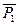 ) = MAZ (
) = MAZ (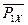 ) + MAZ (
) + MAZ (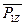 );
);
MAX (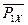 ) = 0 т.к.
) = 0 т.к. 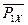 || AX;
|| AX;
MAZ (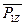 ) = 0 т.к.
) = 0 т.к. 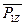 || AZ;
|| AZ;
Из уравнения 5) определяем численное значение силы 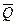 :
:
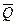 =
= 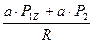 =
= 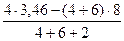 = – 5,51 кН;
= – 5,51 кН;
Подставляя найденную 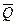 , из уравнение 6) находим величину реакции
, из уравнение 6) находим величину реакции 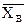 :
:
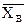 =
= 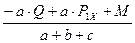 = –
= – 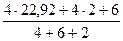 = – 6,47 кН;
= – 6,47 кН;
Из уравнения 4) находим численное значение реакции 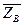 :
:
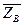 =
= 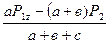 =
= 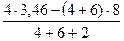 = – 5,51 кН;
= – 5,51 кН;
Подставляя найденную 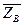 , из уравнения 3) находим численное значение
, из уравнения 3) находим численное значение 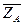 :
:
ZA = P1Z – ZB = 3,46 – 8– (–5,51) = 0,97 кН;
Подставляя найденные 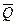 и
и 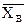 , из уравнения 1) вычисляем реакцию
, из уравнения 1) вычисляем реакцию 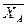 :
:
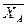 = Q + P1X – XB = 22,92 + 2 – (–6,47) = 31,39 кН;
= Q + P1X – XB = 22,92 + 2 – (–6,47) = 31,39 кН;
2-й способ решения:
∑МAX(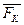 )=0; – а·P1Z+(a+в)P2+(a+в+c)ZB=0; (1)
)=0; – а·P1Z+(a+в)P2+(a+в+c)ZB=0; (1)
∑МAY(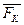 )=0; –R·Q+a·P1Z+aP2=0; (2)
)=0; –R·Q+a·P1Z+aP2=0; (2)
∑МAZ(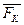 )=0; –aQ+a·P1X+M– (a+в+c)XВ=0; (3)
)=0; –aQ+a·P1X+M– (a+в+c)XВ=0; (3)
∑МВХ(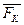 )=0; –с·Р2+(в+с)·P1Z – (a+в+с)ZA=0; (4)
)=0; –с·Р2+(в+с)·P1Z – (a+в+с)ZA=0; (4)
∑МBY(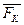 )=0; –R·Q+a·P1Z+a·P2=0; (5)
)=0; –R·Q+a·P1Z+a·P2=0; (5)
∑МBZ(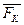 )=0; М – (в+с)·Р1Х+(а+в+с)ХА – (2а+в+с)·Q=0; (6)
)=0; М – (в+с)·Р1Х+(а+в+с)ХА – (2а+в+с)·Q=0; (6)
Из уравнения 1) определяем численное значение реaкции 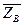 :
:
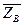 =
= 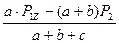 =
= 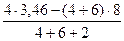 = – 5,51 кН;
= – 5,51 кН;
Из уравнения 4) вычисляем реакцию 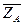 :
:
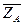 =
= 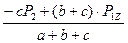 =
= 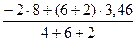 = 0,97 кН;
= 0,97 кН;
Уравнения 2) и 5) дублируют друг друга => численное значение 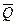 находим из уравнения 2):
находим из уравнения 2):
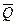 =
= 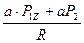 =
= 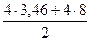 = 22,92 кН;
= 22,92 кН;
Подставляя найденную 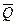 из уравнения 3) вычисляем реакцию
из уравнения 3) вычисляем реакцию 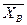 ;
;
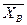 =
= 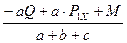 =
= 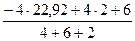 = – 6,47 кН;
= – 6,47 кН;
Подставляя найденную 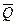 ,из уравнения 6) находим численное значение реакции
,из уравнения 6) находим численное значение реакции 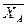 :
:
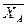 =
= 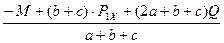 =
= 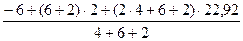 = 31,39 кН;
= 31,39 кН;
Проверка:
∑FKcx1=0; – Q+XA – P1X+XB=0;
–22,92+31,39 –2 – 6,47=0
–31,39+31,39=0
0 ≡ 0
∑FKcz1=0: ZA – P1Z+P2+ZB=0;
0,97 – 3,46+8 – 5,51=0;
8,97 – 8,97=0
0 ≡ 0
Результаты расчётов сводим в таблицу 16:
Таблица 16.
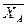 , кН , кН
| 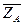 , кН , кН
| 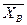 , кН , кН
| 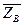 , кН , кН
| 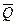 , кН , кН
|
| 31,39 | 0,97 | – 6,47 | – 5,51 | 22,92 |
Вопросы для самопроверки:
1. Виды связей и их реакции (пространственные опоры)?
2. Всякая ли система имеет равнодействующую?
3. Аналитическая форма условий равновесия пространственной системы: а) сходящихся сил? б) параллельных сил? в) произвольной системы сил?
4. Алгебраический момент силы относительно оси? Основные свойства момента?
5. Вектор – момент силы относительно оси и его свойства?
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 732; Нарушение авторских прав?; Мы поможем в написании вашей работы!