Распределение эмпирических данных

В психологических измерениях

Применение статистических методов

В каждой метрической шкале применяются определенные статистические методы. Параметрическая статистика применяется в интервальной и более мощных шкалах.

В ходе любого социального исследования, связанного с применением статистики и теории вероятностей, проводится изучение большого числа людей, их признакового пространства, для того чтобы сделать обобщения и типологические выводы относительно всей или части наблюдаемой популяции. Эта популяция в психометрии (и в других точных математических дисциплинах) называется генеральной совокупностью. Психолог не в состоянии изучить свойства всей популяции. Поэтому он работает с выборкой (частью популяции, группой), а выводы с учетом определенных процессуальных правил распространяет на всю генеральную совокупность. Таким образом, исследователь, изучая свойства относительно небольшой группы, получает знание о свойствах генеральной совокупности. Согласно теореме Бернулли «при бесконечном увеличении объема выборки эмпирическое распределение по вероятности стремится к распределению теоретическому»*.

Характеристики распределения генеральной совокупности называются параметрами, а характеристики выборочного распределения — оценками параметров. Для применения методов параметрической статистики осуществляется процедура определения вида статистического распределения эмпирических данных.

Метод наименьших квадратов в сочетании с гауссовским (нормальным) распределением эмпирических данных служит основой классической статистики. Предположения о нормальном распределении данных имеют "модельный" характер. На деле они не могут выполняться абсолютно точно.

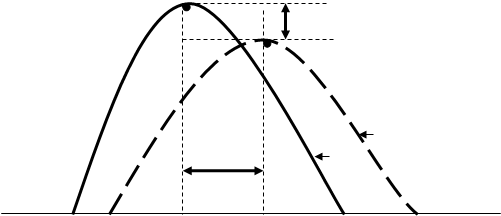
Статистические выводы, составленные на основе модели, приближенной к нормальному распределению, также имеют более или менее приближенный характер. Оценка "приближенности" практической кривой к параметрам нормали** осуществляется при помощи расчета а) асимметрии и эксцесса и б) критериев согласия Пирсона (Хи-квадрат), Колмогорова (1933) и Ястремского (1949). В первом случае оценивается положение вершины практической кривой относительно теоретической, во втором — определенных "участков" (групп частот) практической кривой относительно теоретической нормали.

Коэффициент асимметрии (A_s) показывает величину смещения вершины эмпирической кривой относительно расчетной вершины по горизонтали (вправо "+"; влево "-"). Коэффициент эксцесса (E_x) определяет "крутизну" практической кривой (то есть смещение по вертикали — вверх "+"; вниз "-") (рис. 6).

Коэффициент асимметрии рассчитывается по следующим формулам:

1) A_s = 1 /(nG³)*[ ∑x_i³ — ∑ x_i/n (3∑ x_i² — 2 ((∑x_i)²/n) ], [2]

где n — количество испытуемых, подвергнутых процедуре тестирования;

G = √ [∑x_i ² — (∑ x_i)² / n]/(n — 1),

где x_i — конкретный тестовый балл i-го тестируемого.

Е_х

Дата добавления: 2015-06-04