Дифракция Фраунгофера на щели

Рассмотрим дифракцию плоских волн на щели. Уравнение падающей на преграду плоской волны

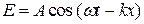, (5.1)

где 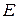и 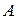– мгновенное и максимальное (амплитудное) значения векторов напряженности электрической составляющей электромагнитной волны.

Рис. 5.1 Схема наблюдения дифракции Фраунгофера на щели

Для аналитического расчета интенсивности света, распространяющегося по разным направлениям за щелью, напишем выражение для волны, посылаемой каждым элементом волнового фронта, и просуммируем действие всех элементов. Согласно волновому принципу Гюйгенса-Френеля световое поле за щелью найдется как результат интерференции когерентных вторичных волн, исходящих из различных точек волнового фронта на щели ширины b (рис. 5.1).

Участок фронта волны шириной 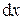испускает вторичные волны. При расчете колебаний, возбуждаемых этими вторичными волнами в произвольной точке на экране необходимо учесть разность фаз между волнами, исходящими из различных элементарных зон.

Световое возмущение в соответствующем участке щели выразится следующим соотношением:

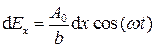, (5.2)

где A ₀ – амплитуда волны, посылаемой всей щелью по направлению 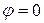, b – ширина щели.

Тогда, колебание, возбуждаемое элементарной зоной 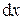с координатой x в точке P, положение которой определяется углом дифракции j, описывается следующим уравнением

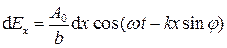(5.3)

Результирующее возмущение в точке P определится как сумма этих возмущений, т.е. интегралом по всей ширине щели b:

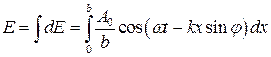. (5.4)

После интегрирования получаем

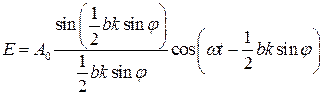. (5.5)

Из выражения (5.5) следует, что амплитуда результирующей волны, идущей в направлении j, описывается следующим уравнением

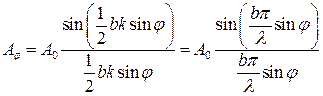. (5.6)

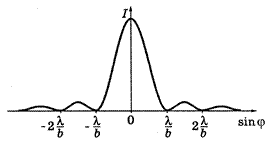
Рис. 5.2. График функции (5.7)

Энергия волны пропорциональна квадрату амплитуды, поэтому интенсивность света в точке P на экране:

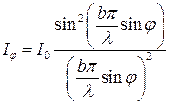, (5.7)

где 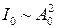, 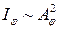. График функции 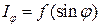представлен на (рис5.2)

Условия максимумов и минимумов интенсивности следуют из (5.7):

а) главный максимум 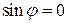при этом ;

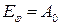б) максимумы первого, второго и других порядков

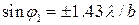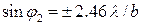, , …; (5.8)

в) минимумы m -го порядка

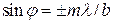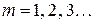, (5.9)

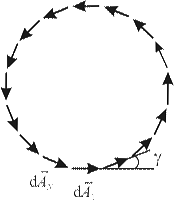
Получим условие минимумов методом векторной диаграммы (метод амплитуд). Разобьем мысленно щель на N очень узких одинаковых по ширине зон-полосок, параллельных прямолинейным краям щели. Колебания, приходящие в точку Р от каждой такой зоны-полоски имеют одинаковую амплитуду d A, разность фаз между колебаниями, приходящими от соседних зон-полосок, так же будет одинакова.

Рис. 5.3. Векторная диаграмма.

Отсюда следует, что при графическом изображении мы получим цепочку векторов 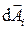одинаковых по модулю и повернутых относительно друг друга на один и тот же угол . Если разность хода крайних лучей составляет 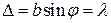, то при 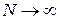разность фаз колебаний, приходящих от первой и последней зоны, 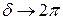. По сути угол 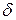– это угол между векторам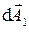и и 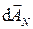. При этом цепочка векторов оказывается замкнутой и амплитуда результирующего колебания обращается в нуль (рис.5.3). Это первый минимум дифракционной картины.

Результирующая амплитуда обращается в нуль и тогда, когда разность фаз от крайних элементов щели 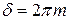, где 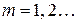Цепочка при этом замыкается после m оборотов. При этом разность хода крайних лучей будет определяться по формуле 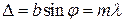, что и является условием минимума.

Дата добавления: 2015-06-04