
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретическое введение. Изучение магнитного поля соленоида с помощью датчика Холла
|
|
|
|
Изучение магнитного поля соленоида с помощью датчика Холла
Цель работы - познакомиться с холловским методом измерения индукции магнитного поля.
В пространстве, окружающем проводники с током или движущиеся заряда, возникает магнитное поле, которое можно обнаружить по воздействию его на другой проводник с током или магнитную стрелку. Магнитной поле в каждой точке пространства количественно может быть описано с помощью вектора напряженности магнитного поля  или с помощью вектора индукции магнитного поля
или с помощью вектора индукции магнитного поля 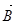 . В вакууме векторы
. В вакууме векторы 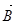 и
и 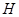 связаны соотношением
связаны соотношением
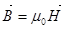 (4.1)
(4.1)
где  Гн/м – магнитная постоянная.
Гн/м – магнитная постоянная.
Для вычисления напряженности и индукции магнитного поля используют закон Био - Савара - Лапласа, согласно которому элементарная напряженность магнитного поля  , создаваемая элементом проводника с током
, создаваемая элементом проводника с током  в некоторой точке пространства на расстоянии
в некоторой точке пространства на расстоянии  , определяется выражением
, определяется выражением
 (4.2)
(4.2)
Для нахождения результирующей напряженности, создаваемой проводником конечных размеров, надо воспользоваться принципом суперпозиции магнитных полей и найти векторную сумму элементарных напряженностей 
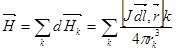 (4.3)
(4.3)
 В пределе сумма записывается в виде интеграла по контуру проводника с током. Применим формулу (4.3) для вычисления напряженности магнитного поля на оси соленоида. Каждый виток соленоида - это круговой ток, поэтому первоначально вычислим напряженность поля на оси кругового витка с током (рис. 4.1). При сложении составляющих магнитного поля
В пределе сумма записывается в виде интеграла по контуру проводника с током. Применим формулу (4.3) для вычисления напряженности магнитного поля на оси соленоида. Каждый виток соленоида - это круговой ток, поэтому первоначально вычислим напряженность поля на оси кругового витка с током (рис. 4.1). При сложении составляющих магнитного поля 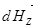 , перпендикулярных оси ОА, они компенсируют друг друга вследствие симметрии контура. Поэтому результирующая напряженность магнитного поля в точке А направлена вдоль оси кругового тока и равна по модулю:
, перпендикулярных оси ОА, они компенсируют друг друга вследствие симметрии контура. Поэтому результирующая напряженность магнитного поля в точке А направлена вдоль оси кругового тока и равна по модулю:
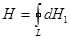 (4.4)
(4.4)
 (4.5)
(4.5)
В (4.5) учтено, что векторы  и
и  взаимно перпендикулярны. Подставляя (4.5) в (4.4) и учитывая, что величины
взаимно перпендикулярны. Подставляя (4.5) в (4.4) и учитывая, что величины  и
и  постоянны, имеем
постоянны, имеем
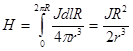 (4.6)
(4.6)
Перейдем теперь к вычислению поля соленоида, изображенного на рис. 4.2. Пусть на единицу длины соленоида приходится  . витков, тогда на участке
. витков, тогда на участке 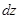 будет
будет 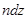 витков, которые в точке 0 соленоида согласно (4.6) создадут напряженность
витков, которые в точке 0 соленоида согласно (4.6) создадут напряженность
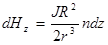 (4.7)
(4.7)
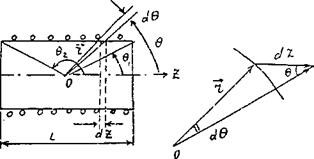
Рис. 4.2 Рис. 4.3
На рис. 4.3 отдельно изображены элемент 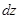 , радиус-вектор
, радиус-вектор  и углы
и углы  и
и 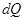 . Из геометрических построений рис. 4.2 и 4.3 следует:
. Из геометрических построений рис. 4.2 и 4.3 следует:
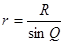 ,
,  (4.8)
(4.8)
Подставляем (4.8) в (4.7) и интегрируем в пределах от 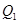 до
до  :
:
 (4.9)
(4.9)
В случае бесконечного соленоида
 ,
,  ,
,  (4.10)
(4.10)
ПРИБОРЫ И ОБОРУДОВАНИЕ
ИП - источник питания,
PV - цифровой вольтметр,
ФПЗ-04 - модуль,
С - соленоид,
Ш - шток с нанесенной шкалой и закрепленным на торце датчиком Холла.
МЕТОД ИЗМЕРЕНИЯ
 Для экспериментального исследования напряженности магнитного поля на оси соленоида в настоящей работе используется метод, оснований на явления Холла. Если через проводящую пластинку поперечным сечением
Для экспериментального исследования напряженности магнитного поля на оси соленоида в настоящей работе используется метод, оснований на явления Холла. Если через проводящую пластинку поперечным сечением  пропустить ток плотностью
пропустить ток плотностью  и поместить ее в поперечное магнитное поле с индукцией
и поместить ее в поперечное магнитное поле с индукцией 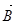 , то перпендикулярно векторам
, то перпендикулярно векторам  и
и 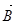 создается электрическое пола напряженностью
создается электрическое пола напряженностью 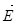 (рис. 4.4). Возникающая при этом разность потенциалов
(рис. 4.4). Возникающая при этом разность потенциалов 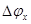 (ЭДС Холла) пропорциональна величине тока и индукции магнитного поля:
(ЭДС Холла) пропорциональна величине тока и индукции магнитного поля:
 (4.11)
(4.11)
где 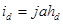
Коэффициент пропорциональности  называется постоянной Холла. В работе используется полупроводниковый датчик Холла марки X50I с управляющим током
называется постоянной Холла. В работе используется полупроводниковый датчик Холла марки X50I с управляющим током 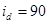 мА, поскольку постоянная Холла для полупроводников значительно больше чем для проводников.
мА, поскольку постоянная Холла для полупроводников значительно больше чем для проводников.
Силовые линии магнитного поля на оси соленоида направлены вдоль оси, поэтому датчик Холла должен располагаться на торце специального штока, вставляемого в соленоид. Толщина датчика  в направлении магнитного поля равна 0,2 мм. Для измерения положения летчика внутри соленоида па боковой грани штока нанесена миллиметровая шкала.
в направлении магнитного поля равна 0,2 мм. Для измерения положения летчика внутри соленоида па боковой грани штока нанесена миллиметровая шкала.
При отсутствии магнитного поля ЭДС Холла должна быть равна нулю. Однако вследствие различных побочных явлений, например недостаточно точной установки выходных электродов датчика, измерительный прибор может показать некоторую разность потенциалов даже при отсутствии тока в соленоиде. Для исключения погрешностей измерения проводят дважды при двух противоположных направлениях тока в соленоиде. Тогда  . Однако в данной работе изменение направления тока в соленоиде не предусмотрено. Поэтому погрешность в определении
. Однако в данной работе изменение направления тока в соленоиде не предусмотрено. Поэтому погрешность в определении  указана на модуле ФПЭ-04.
указана на модуле ФПЭ-04.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОШ
 |
Задание I. Определение зависимости магнитной индукции в средней точке на оси соленоида и тарировка датчика Холла.
1. Собрать схему, изображенную на рис. 4.5 и 4.6
2. Поставить шток с датчиком Холла в среднее положение на оси соленоида ("0" по шкале).
3. Включить источник питания я цифровой вольтметр в сеть 220 В. Измерить ЭДС Холла в центре соленоида для токов 0,5; 1,0; 1,5; 2,0 А, при этом из измеренного значения необходимо вычесть поправку  , указанную на модуле;. Данные занести в таблицу 4.1.
, указанную на модуле;. Данные занести в таблицу 4.1.
Таблица 4.1
| № измерения | Ток соленоида
 , А , А
| ЭДС датчика
Холла
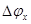 , В , В
| Индукция
 , Тл , Тл
| Постоянная Холла
 , В∙м/ТлА , В∙м/ТлА
|
4. Вычислить индукцию магнитного поля для заданных значений силы тока  по формулам (4.10) и (4.1); данные занести в таблицу.
по формулам (4.10) и (4.1); данные занести в таблицу.
5. Вычислить значения постоянной Холла  для каждого измерения по формуле (4.11); данные занести в таблицу. Найти среднее значение
для каждого измерения по формуле (4.11); данные занести в таблицу. Найти среднее значение  .
.
6. Построить графики зависимости  и
и  по данным табл. 4.1.
по данным табл. 4.1.
Задание 2. Исследование зависимости индукции магнитного поля от координаты  , отсчитываемой от средней точки.
, отсчитываемой от средней точки.
1. Установить величину тока в катушке соленоида по указанию преподавателя.
2. Перемещая шток с датчиком Холла вдоль оси соленоида с интервалом 1 см, измерить ЭДС Холла. Полученные данные занести в таблицу 4.2.
Таблица 4.2
Положение датчика  , мм , мм
| |||||||
| ЗДС датчика Холла, В | |||||||
| Индукция Тл |
3. Вычислить индукцию поля В для каждого положения датчика Холла по формуле (4.11). При расчете использовать значение  , полученное в задании I. Данные занести в табл. 4.2.
, полученное в задании I. Данные занести в табл. 4.2.
4. Построить график зависимости 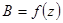 по данным табл. 4.2.
по данным табл. 4.2.
5. Повторить измерения в расчеты по пи. 2-4 для нового значения  (по заданию преподавателя).
(по заданию преподавателя).
6. Для одного из полученных значений  рассчитать абсолютную и относительную погрешности измерения.
рассчитать абсолютную и относительную погрешности измерения.
КОНТРОЛЬНА ВОПРОСЫ
1. Сформулируйте закон Био - Савара - Лапласа. Пользуясь этим законом, дайте вывод формулы для индукции магнитного поля на оси кругового витка с током.
2. Сформулируйте теорему о циркуляции вектора  по контуру
по контуру 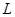 . Пользуясь этой теоремой, дайте вывод формулы для индукции магнитного поля бесконечною соленоида.
. Пользуясь этой теоремой, дайте вывод формулы для индукции магнитного поля бесконечною соленоида.
3. Пользуясь принципом суперпозиции, дайте вывод формулу для магнитного ноля бесконечного соленоида.
4. Дайте вывод формулы для ЭДС Холла.
5. Нарисуйте схему измерений для исследования зависимости 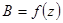
Литература [I, 3,4].
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1052; Нарушение авторских прав?; Мы поможем в написании вашей работы!