Z-матрица

Формат файла

Формат файла, первоначально используемый PDB, назвали форматом файла PDB. Этот оригинальный формат был ограничен шириной компьютерных перфокарт до 80 характеристик на линию. Приблизительно в 1996 начал постепенно вводиться "макромолекулярный Кристаллографический информационный формат" файла, mmCIF. В 2005 была описана версия XML этого формата, названного PDBML. Структурные файлы могут быть загружены в любой из этих трех форматов. Фактически, отдельные файлы легко загружаются в графические пакеты, используя веб-адреса:

• Для файлов формата PDB используйте, например, http:// www.pdb.org/pdb/files/4hhb.pdb.gz

• Для PDBML (XML) файлы, используйте, например, http:// www.pdb.org/pdb/files/4hhb.xml.gz

"4hhb" – идентификатор PDB. Каждая структура, изданная в PDB, получает четырехсимвольный алфавитно-цифровой идентификатор, его ID номер PDB. (Он не может использоваться в качестве идентификатора для биомолекул, потому что часто несколько структур для той же самой молекулы — в различной окружающей среде или конформациях — содержатся в PDB с различными ID PDB.)

Следующим методом для представления молекулы в 3D пространстве является использование внутренних координат, таких как длины связей, углы связей и двугранные углы. Двугранный угол образуется из четырех атомов и помогает определить размер молекулы. Под связью в данном случае подразумевают не химическую связь, а просто вектор, направленный от одного атома к другому, хотя они могут и совпадать.

Наиболее широкоиспользуемый способ описания молекулы ее внутренними координатами – это так называемая Z-матрица. Z-матрица называется так потому, что второй атом всегда располагается вдоль оси аппликат (оси Z). Внутренние координаты описывают пространственное расположение атомов относительно других атомов. Рис. 2.91 иллюстрирует такое представление для 1,2-дихлорэтана.

Рис. 2.91. Внутренние координаты 1,2-дихлорэтана: длины связей r1 и r2, угол связи α и двугранный угол τ.

Сущность этого способа представления координат состоит в конструировании для каждого задаваемого атома своей собственной полярной системы координат. Для этой цели используются любые три атома, положение которых было определено ранее. Эти атомы называются базисными, причем первый базисный атом принимается за центр полярной системы координат, второй базисный атом задает базовую ось, а третий базисный атом – базовую плоскость полярной системы координат.

Для однозначного определения положения атома 4 в пространстве необходимо определить совокупность трех координат: радиус-вектора r, плоского угла θ и двугранного угла φ. Как видно из схемы, величина r находится из расстояния между задаваемым атомом 4 и базисным атомом 1, плоский угол θ – суть угол между атомами 4, 1 и 2 с вершиной на базисном атоме 1, двугранный (межплоскостной, диэдральный, торсионный) угол φ – это угол между плоскостями 4, 1, 2 и 1, 2, 3, т.е. угол между перпендикулярами к базовой оси, опущенными из одной точки в обе плоскости.

Из сказанного следует, что нельзя использовать базисные атомы, лежащие на одной прямой, т.к. в этом случае базовая плоскость 1, 2, 3 однозначно не определена и, следовательно, угол φ не может быть рассчитан. По этой же причине следует выбирать базисные атомы 1 и 2 таким образом, чтобы угол θ (4-1-2) не был равен 0 или 180 градусам, т.к. в этом случае однозначно не определяется плоскость 4, 1, 2.

Задачей пользователя является разумный выбор базисных атомов с целью приближенного определения величин r, θ и φ. В ходе последующего расчета программа найдет оптимальные значения геометрических параметров.

На рис. 2.92 показана Z-матрица 1,2-дихлорэтана.

C1
C2	1.5
C13	1.7
H4	1.1				– 60
H5	1.1
C16	1.7
H7	1.1				– 60
H8	1.1

Рис. 2.92. Z-матрица 1,2-дихлорэтана

Каждая линия в Z-матрице представляет один атом молекулы. В первой линии атом 1 определяется как С1, т.е. этот углеродный атом лежит в начале координатной системы. Второй атом С2 находится на расстоянии 1,5 Å (вторая колонка) от атома 1 (третья колонка) и должен всегда помещаться на главной оси (x -ось на рис. 2.92). Третий атом (хлор) Cl3 должен лежать на xy -плоскости; он находится на расстоянии 1,7 Å от атома 1, и угол α между атомами 3-1-2 составляет 109º (четвертая и пятая колонка). Третий тип внутренней координаты (двугранный угол τ) вводится на четвертой линии Z-матрицы в шестой и седьмой колонках. Это угол между плоскостями, которые образованы атомами 4,2,1 и 2,1,3 (xy -плоскость). За исключением первых трех атомов, каждый атом описывается набором трех внутренних координат: расстояние от предыдущего определенного атома, угол связи, образованной атомом с двумя предыдущими атомами и двугранный угол атома с тремя предыдущими. Число (3N – 6) внутренних координат, где N – число атомов в молекуле, представляет структуру в 3D пространстве, а также соответствует числу степеней свободы молекулы.

Z-матрица может быть преобразована в декартовые координаты. Также возможно и обратное преобразование без потери информации как показано на примере метана (рис.).

Молекула метана в декартовых координатах (в ангстремах):

C 0.000000 0.000000 0.000000H 0.000000 0.000000 1.089000H 1.026719 0.000000 -0.363000H -0.513360 -0.889165 -0.363000H -0.513360 0.889165 -0.363000

Молекула метана в виде z-матрицы:

CH 1 1.089000 H 1 1.089000 2 109.4710 H 1 1.089000 2 109.4710 3 120.0000 H 1 1.089000 2 109.4710 3 -120.0000

Рис. 3333 Представление молекулы метана

Разберем представление разных молекул в виде Z-матриц. Внешний вид этих матриц также может отличаться, однако сущность этого метода не изменяется.

Z-матрицу этаналя можно изобразить следующим образом:

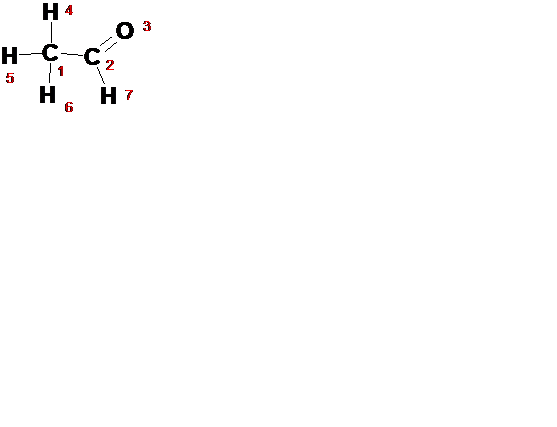
	УГОЛ	λ, Å	Номер, от которого измеряется	Валентный угол	Номер, от которого измеряется	Двугранный угол	Номер, от которого измеряется
	H
	C	1.49
	C	1.22
	H	3.00
	H	1.09
	H	1.09				- 60
	H	1.09

Z-матрица этанола имеет следующий вид:

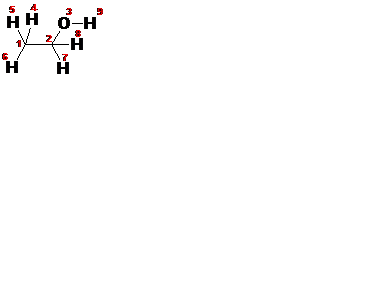
Name: MOPAC file created on 9/2 15:15:47 1994 by HYPERCHEM C 00000.0000 0 00000.0000 0 00000.0000 0 0 0 0 C 00001.5399 1 00000.0000 0 00000.0000 0 1 0 0 O 00001.4299 1 00109.4710 1 00000.0000 0 2 1 0 H 00001.0900 1 00109.4710 1 00179.9999 1 1 2 3 H 00001.0900 1 00109.4710 1 00299.9994 1 1 2 3 H 00001.0900 1 00109.4714 1 00059.9997 1 1 2 3 H 00001.0900 1 00109.4709 1 00299.9994 1 2 1 4 H 00001.0900 1 00109.4714 1 00059.9997 1 2 1 4 H 00000.9599 1 00109.4710 1 00060.0005 1 3 2 7

координата 1 координата 2 координата 3 связь с атомом валентный угол двугранный угол

В качестве другого примера также можно привести более сложную молекулу фенилаланина.

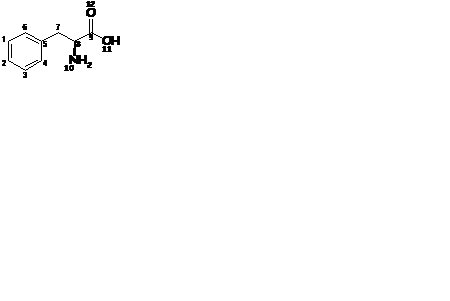
Name:

MOPAC file created on 3/10 13:19:25 2007 by HYPERCHEM

C 0.0000 0 000.0000 0 000.0000 0 0 0 0

C 1.4000 1 000.0000 0 000.0000 0 1 0 0

C 1.4000 1 119.9999 1 000.0000 0 2 1 0

C 1.4000 1 119.9999 1 000.0000 1 3 2 1

C 1.3999 1 119.9999 1 000.0000 1 4 3 2

C 1.3999 1 120.0000 1 000.0000 1 5 4 3

C 1.5200 1 119.9999 1 179.9999 1 5 4 3

C 1.5399 1 109.4709 1 000.0000 1 7 5 6

C 1.5200 1 109.4710 1 179.9999 1 8 7 5

N 1.4700 1 109.4710 1 299.9994 1 8 7 5

O 1.3599 1 120.0000 1 180.0000 1 9 8 7

O 1.2199 1 119.9999 1 240.0005 1 9 8 10

H 1.0799 1 120.0000 1 179.9999 1 1 2 3

H 1.0799 1 120.0000 1 179.9999 1 2 1 6

H 1.0799 1 120.0000 1 179.9999 1 3 2 1

H 1.0800 1 119.9999 1 179.9999 1 4 3 2

H 1.0799 1 120.0000 1 179.9999 1 6 5 4

H 1.0900 1 109.4710 1 119.9994 1 7 5 6

H 1.0899 1 109.4714 1 239.9997 1 7 5 6

H 1.0900 1 109.4714 1 300.0002 1 8 7 18

H 1.0100 1 109.4710 1 299.9994 1 10 8 9

H 1.0100 1 109.4709 1 179.9991 1 10 8 20

H 0.9599 1 109.4709 1 000.0000 1 11 9 12

Дата добавления: 2015-06-04