Матрица связей

Матрица связей по виду похожа на матрицу смежности, но в отличие от нее дает информацию еще и о порядке связей связанных атомов. Элементы матрицы получают значение 2, если существует двойная связь между атомами, например атомы 2 и 3 в указанном примере. Остальные значения могут быть 0, 1 или 3 для других комбинаций связей. Это представление является избыточным (рис. 2.17).

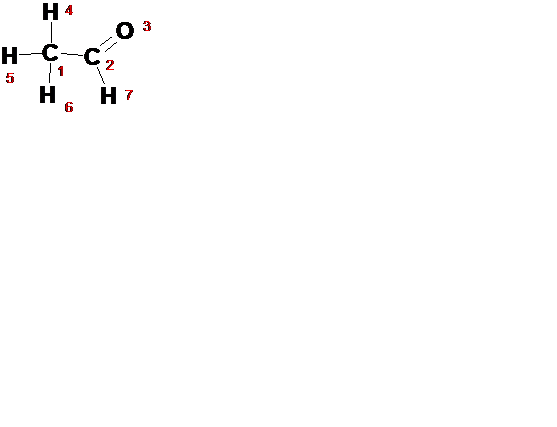
n = 7

a b c

Рис. 2.17. а) избыточная матрица связей этаналя, в которой удалены значения нуля. б) матрица м.б. сжата путем устранения дублей. с) удаление атомов водорода дает простое представление неизбыточной матрицы.

Матрица связей дает такое представление молекулярной структуры, в котором каждый атом, каждая связь и тип связи кодируются по отдельности и всегда обозначаются явным образом. В отличие от линейных номенклатур правила составления матриц связей просты и легко применимы для кодирования структур любой сложности.

Главная диагональ матрицы связей включает коды атомов структуры. Каждому типу атомов сопоставляется свой код. Недиагональный элемент матрицы связей а_у содержит информацию о связи между i -м и j - м атомами и является кодом данного типа связи. Правила кодирования структур в виде матриц связей легко усвоить с помощью нижеследующего примера.

В Таблица 1 приведена структурная формула кофеина и соответствующая ей матрица связей. Также приведены числовые коды различных типов атомов и химических связей. Последовательность нумерации атомов в структуре произвольна и соответствует последовательности расположения кодов атомов на главной диагонали матрицы связей. Атомы водорода не включены, так как их расположение легко рассчитать с помощью правил валентности. Равенство недиагонального элемента а_ij нулю означает отсутствие связи между i -м и j - м атомами.

Таблица 1. Пример кодирования структуры в виде матрицы связей*

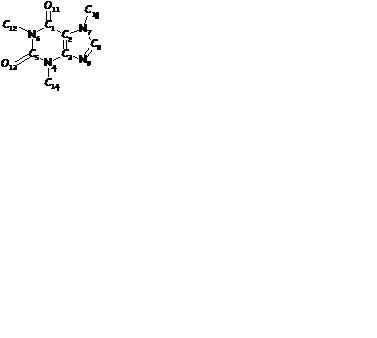
* коды для таблицы см. ниже

Коды для таблицы 9

Использованные в рассмотренном при мере числовые коды выбраны произвольно и не являются общепринятым стандартом. Впрочем, это обстоятельство не создает дополнительных трудностей, так как любая матрица связей легко может быть переведена в другую кодировку с помощью несложной вычислительной процедуры. Кстати, системы линейной кодировки таким свойством не обладают.

Матрица связь – электрон (BE матрица)

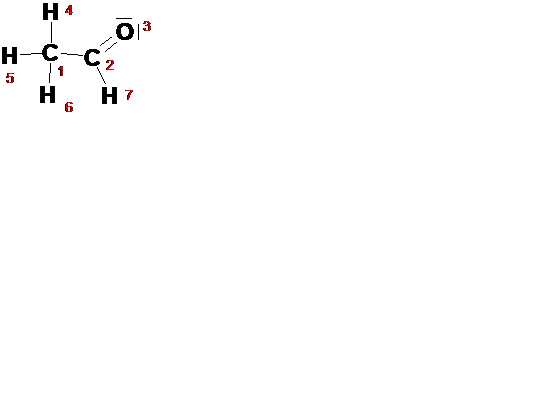Матрица связь – электрон (BE матрица) была предложена в модели Dugundji-Ugi. Ее можно рассматривать как расширение матрицы связей. Этот тип матрицы дает дополнительно число свободных валентных электронов на соответствующем атоме в диагональных элементах (например, О3 = 4 на рис. 2.18).

n = 7 a b c

Рис. 2.18. а) избыточная ВЕ-матрица этаналя с пропущенными значениями нуля. б) матрица м.б. сжата путем удаления дублей. с) удаление атомов водорода обеспечивает простую презентацию неизбыточной матрицы.

В сущности ВЕ-матрица иллюстрирует все валентные электроны атомов в молекуле, но одни из них включены в связи, а другие считаются свободными электронами с атомом. ВЕ-матрица имеет ряд интересных математических свойств, которые напрямую отображают химическую информацию.

В примере на рис. 2.19 атом кислорода имеет 2+4 (ряд) +2+4 (колонка) – 4 (диагональный элемент) = 8 электронов. Это показывает, что атом кислорода подчиняется октетному правилу.

								сумма в ряду	элемент
									C
									C
									O
									H
									H
									H
									H
сумма в колонке
сумма пересечения

Рис. 2.19. ВЕ-матрица позволяет определить число валентных электронов (сумма каждого ряда) на атомах и подтвердить октетное правило.

ВЕ-матрица также обеспечивает основу для представления матрицы химических реакций.

Дата добавления: 2015-06-04