Решение. 1. Откройте новую рабочую таблицу

Решение

1. Откройте новую рабочую таблицу. Установите табличный курсор в ячейку А1.

2. Для определения границ доверительного интервала необходимо на панели ин­струментов Стандартная нажать кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ДОВЕРИТ, после чего нажмите кнопку ОК.

3. В рабочие поля появившегося диалогового окна ДОВЕРИТ с клавиатуры введите условия задачи; Альфа − 0,05; Станд-откл − 2,5; Размер −25 (рис. 1.11). Нажми­те кнопку ОК.

4. В ячейке А1 появится полуширина 95%-ного доверительного интервала для среднего значения выборки — 0,979981. Другими словами, с 95%-ным уровнем надежности можно утверждать, что средняя продолжительность разряда акку­мулятора составляет 140 ± 0,979981 часа или от 139,02 до 140,98 часа.

Рис. 1.1. Пример заполнения диалогового окна «ДОВЕРИТ»

Пример 1.1. Пусть имеется выборка, содержащая числовые значения: 13, 15, 17, 19,22,25,19. Необходимо определить границы 95%-ного доверительного интерва­ла для среднего значения и для нахождения «выскакивающей» варианты.

1. В диапазон А1:А7 введите исходный ряд чисел.

2. Далее вызовите процедуру Описательная статистика. Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появив­шемся списке Инструменты анализа выберите строку Описательная статистика.

3. В появившемся диалоговом окне в рабочем поле Входной интервал: укажите вход­ной диапазон − А 1:А7. Переключателем активизируйте Выходной интервал и ука­жите выходной диапазон — ячейку В1. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в левое поле Уровень надежности: и в правом поле (%) − 95. Затем нажмите кнопку ОК.

4. В результате анализа в указанном выходном диапазоне для доверительной ве­роятности 0,95 получаем значения доверительного интервала (рис. 1.12).

А	В
	Столбец 1
	Уровень надежности (95.0%)	3,770272046

Рис. 1.12. Исходная выборка (А1:А7) и результат вычислений (СЗ) из примера 1.6

Уровень надежности − это половина доверительного интервала для генерального среднего арифметического. Из полученного результата следует, что с вероятнос­тью 0,95 среднее арифметическое для генеральной совокупности находится в интервале 18,571 ± 3,77. Здесь 18,571 − выборочное среднее М для рассматриваемо­го примера, которое находится обычно процедурой Описательная статистика одно­временно с доверительным интервалом.

5. Для нахождения доверительных границ для «выскакивающей» варианты необ­ходимо полученный выше доверительный интервал умножить на (в приме­ре 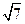, то есть 3,77* 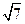=9,975). В «MS Excel» это можно выполнить следующим образом. Табличный курсор установите в свободную ячейку С4; введите с клави­атуры знак =; мышью укажите на ячейку СЗ (в которой находится результат вы­числений); введите с клавиатуры знак *; с панели инструментов Стандартная вы­зовите Мастер функций (кнопка fx); выберите категорию Математические, тип функции Корень; нажмите ОК; введите с клавиатуры число 7 и нажмите ОК. В результате получим в ячейке С4 значение доверительного интервала − 9,975.

Таким образом, варианта, попадающая в интервал 18,571 ± 9,975, считается при­надлежащей данной совокупности с вероятностью 0,95. Выходящая за эти грани­цы может быть отброшена с уровнем значимости = 0,05.

Проверка соответствия теоретическому распределению. Следующей задачей, воз­никающей при анализе одной выборки, является оценка меры соответствия (рас­хождения) полученных эмпирических данных и каких-либо теоретических рас­пределений. Это связано с тем, что в большинстве случаев при решении реальных задач закон распределения и его параметры неизвестны. В то же время применяе­мые статистические методы в качестве предпосылок часто требуют определенного закона распределения.

Наиболее часто проверяется предположение о нормальном распределении генераль­ной совокупности, поскольку большинство статистических процедур ориентировано на выборки, полученные из нормально распределенной генеральной совокупности.

Для оценки соответствия имеющихся экспериментальных данных нормальному закону распределения обычно используют графический метод, выборочные пара­метры формы распределения и критерии согласия.

Графический метод позволяет давать ориентировочную оценку расхождения или совпадений распределений (рис. 1.13).

56 57 58 59 60 61 62 63 64 65

Дата добавления: 2015-06-29