Анализ двух выборок

Упражнения

10. Определите, лежит ли значение 19 внутри границ 95%-ного доверительного интервала выборки 2, 3, 5, 7, 4, 9, 6,4, 9,10,4, 7, 19.

11. Определите с уровнем значимости 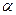= 0,05 максимальное отклонение средне­го значения генеральной совокупности от среднего выборки 3, 4, 4, 2, 5, 3, 4, 3, 5, 4, 3, 5, 1.

12.Найдите соответствие экспериментальных данных нормальному закону рас­пределения для следующей выборки весов детей (кг): 21, 21, 22, 22, 22, 22, 22, 22, 22, 22, 22, 23, 23, 23, 23, 23, 23, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 21, 21, 21, 21, 21, 21, 21, 21, 21, 26, 26, 26, 26, 26, 27, 27.

Выявление достоверности различий. Следующей задачей статистического ана­лиза, решаемой после определения основных выборочных характеристик и ана­лиза одной выборки, является совместный анализ нескольких выборок. Важ­нейшим вопросом, возникающим при анализе двух выборок, является вопрос о наличии различий между этими выборками. Обычно для этого проводят провер­ку статистических гипотез о принадлежности обеих выборок одной генеральной совокупности или о равенстве генеральных средних. В рассмотренном ранее при­мере 1.3. такие различия выявляются путем сравнения данных реализации тур­фирмой путевок за периоды до и после начала активной рекламной компании. Если сопоставить средние значения числа реализованных за месяц путевок до (125,6) и после (145,7) начала рекламной компании, видно, что они различают­ся. Можно ли по этим данным сделать вывод об эффективности рекламной ком­пании?

Для решения задач такого типа используются так называемые критерии различия. Для проверки одной и той же гипотезы могут быть использованы разные статис­тические критерии. Правильный выбор критерия определяется как спецификой данных и проверяемых гипотез, так и уровнем статистической подготовки иссле­дователя.

Статистические критерии различия подразделяются на параметрические и непа­раметрические критерии. Параметрические критерии служат для проверки гипо­тез о параметрах определенных распределений генеральной совокупности (чаще всего нормального распределения). Непараметрические критерии для проверки гипотез не используют предположений о законе распределения генеральной сово­купности и не требуют знания параметров распределения.

Параметрические критерии. Параметрические критерии служат для проверки гипотез о положении и рассеивании. Из параметрических критериев наибольшей популярностью при проверке гипотез о равенстве генеральных средних (матема­тических ожиданий) пользуется f-критерий Стьюдента (t-критерий различия).

Критерий Стьюдента (t) наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности». Критерий по­зволяет найти вероятность того, что оба средних относятся к одной и той же сово­купности. Если эта вероятность р ниже уровня значимости (р < 0,05), то принято считать, что выборки относятся к двум разным совокупностям.

При использовании t-критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух неза­висимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и опытная группа, состоящие, например, из разных пациентов, количество которых в группах может быть различно.

Во втором случае, когда одна и та же группа объектов порождает числовой матери­ал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными. Например, измеряет­ся содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения определенной дозой излучения.

В обоих случаях в принципе должно выполняться требование нормальности рас­пределения исследуемого признака в каждой из сравниваемых групп и равенства дисперсий в сравниваемых совокупностях. Однако на практике по большому сче­ту корректное применение t-критерия Стьюдента для двух групп часто бывает за­труднительно, поскольку достоверно проверить эти условия удается далеко не всегда.

Для оценки достоверности отличий по критерию Стьюдента принимается нуле­вая гипотеза, что средние выборок равны между собой. Затем вычисляется значе­ние вероятности того, что изучаемые события (например, количества реализован­ных путевок в обеих выборках) произошли случайным образом.

В MS «MS Excel» для оценки достоверности отличий по критерию Стьюдента использу­ются специальная функция «ТТЕСТ» и процедуры пакета анализа (см. раздел «Ис­пользование Пакета анализа для выявления различий» ниже).

Все перечисленные инструменты вычисляют вероятность, соответствующую кри­терию Стьюдента, и используются, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же сред­нее.

Функция «ТТЕСТ» использует следующие параметры: ТТЕСТ (массив1; массив2; хвосты; -тип). Здесь:

О массив 1 − это первое множество данных;

О массш2 − это второе множество данных;

О хвосты − число хвостов распределения. Обычно число хвостов равно 2;

О тип − это вид исполняемого t- теста. Возможны 3 варианта выбора: 1 − пар­ный тест, 2 − двухвыборочный тест с равными дисперсиями, 3 − двухвыборочный тест с неравными дисперсиями.

Пример 1.8. Выявить, достоверны ли отличия при сравнении данных реализации турфирмой путевок за периоды до и после начала активной рекламной компании (см. пример 1.3).

Дата добавления: 2015-06-29