Решение. 1. Введите данные (как в пункте 1 примера 1.3)

1. Введите данные (как в пункте 1 примера 1.3).

2. Для выявления достоверности отличий табличный курсор установите в сво­бодную ячейку (А11). На панели инструментов необходимо нажать кнопку Встав­ка функции (f_х). В появившемся диалоговом окне Мастер функций выберите кате­горию Статистические и функцию ТТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ТТЕСТ за серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы в поле Массив 1 (А2:А8). В поле Массив 2 введите диапазон данных исследуемой группы (В2:В8). В поле Хвосты всегда вводится с клавиатуры цифра 2 (без кавычек), а в поле Тип с клавиатуры введи­те цифру 3. Нажмите кнопку ОК. В ячейке А11 появится значение вероятнос­ти - 0,006295.

3. Поскольку величина вероятности случайного появления анализируемых вы­борок (0,006295) меньше уровня значимости (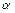 = 0,05), то нулевая гипотеза отвергается. Следовательно, различия между выборками не случайные и сред­ние выборок считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия Стьюдента можно сделать вывод о боль­шей эффективности реализации путевок после начала рекламной компании (р < 0,05).

Как указывалось выше, при использовании t-критерия выделяют два основных случая. В первом случае его применяют для проверки гипотезы о равенстве гене­ральных средних двух независимых, несвязанных выборок (так называемый двух­выборочный t-критерий). В этом случае есть две различных выборки, количество элементов в которых может быть также различно. При заполнении диалогового окна ТТЕСТ при этом указывается Тип 3.

Во втором случае, когда одна и та же группа объектов порождает числовой матери­ал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными (при заполнении диалогового окна ТТЕСТ указывается Тип 1 ). Например, сравнивается реализация путевок двумя фирмами в соответствующие месяцы. В качестве упражнения рассмотрим пример.

Пример 1.9. Сравнивается количество наличных денег у двух групп студентов (в рублях);

А	В

Необходимо определить достоверность различия между группами при двух вари­антах постановки задачи:

О группы состоят из различных студентов (тип 3);

О группы состоят из одних и тех же студентов, но первая − до посещения буфета, а вторая − после (тип 1).

Решение. В ячейки С1:С5введите количество денег у студентов первой группы. В ячейки D1:D5 введите количество денег у студентов второй группы,

1. Табличный курсор установите в свободную ячейку (С6). На панели инстру­ментов необходимо нажать кнопку Вставка функции (f_x). В появившемся диа­логовом окне Мастер функций выберите категорию Статистические и функцию ТТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ТТЕСТ за
серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши ввести диапазон данных первой группы в поле Массив 1 (С1:С5). В поле Массив 2 введите диапазон данных второй группы (D1:D5). В поле Хвосты всегда вводится цифра 2 (без кавычек), а в поле Тип введите цифру 3. Нажмите кнопку ОК. В ячейке С6 появится значение вероят­ности - 0,228053.

Поскольку величина вероятности случайного появления анализируемых вы­борок (0,228053) больше уровня значимости (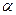 = 0,05), то нулевая гипотеза не может быть отвергнута (принимается). Следовательно, различия между выбор­ками могут быть случайными и средние выборок не считаются достоверно от­личающимися друг от друга. Поэтому на основании применения критерия Стьюдента нельзя сделать вывод о достоверности отличий двух групп студентов по количеству карманных денег, имеющихся у них (р > 0,05).

3. Табличный курсор установите в свободную ячейку (D6). На панели инстру­ментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ТТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ТТЕСТ за серое поле
мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кноп­ке). Указателем мыши введите диапазон данных первой группы в поле Массив 1 (С1:С5). В поле Массив 2 введите диапазон данных второй группы (D1:D5). В поле Хвосты всегда вводится цифра 2 (без кавычек), а в поле Тип введите
цифру 1. Нажмите кнопку ОК. В ячейке D6 появится значение вероятности − 0,003883.

Поскольку величина вероятности случайного появления анализируемых выборок (0,003883) меньше уровня значимости (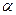 = 0,05), то нулевая гипотеза отвергается. Следовательно, различия между выборками не могут быть случайными и средние выборок считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия Стьюдента можно сделать вывод о том, что в двух группах студентов выявлены достоверные отличия по количеству карманных де­нег (р < 0,05), что явилось результатом посещения буфета.

Таким образом, ясно, что применение различных типов критерия Стьюдента мо­жет приводить к различным результатам на основании одних и тех же исходных данных. Можно предложить следующий приблизительный способ выбора типа критерия: если не ясно, какой тип критерия выбирать, выбирается тип 3; если оче­видно, что выборки зависимы, связаны (например, это одни и те же студенты), то следует выбирать тип 1.

Критерий Фишера. Критерий Фишера используют для проверки гипотезы о при­надлежности двух дисперсий одной генеральной совокупности и, следовательно, их равенстве. При этом предполагается, что данные независимы и распределены по нормальному закону. Гипотеза о равенстве дисперсий принимается, если отно­шение большей дисперсии к меньшей меньше критического значения распределе­ния Фишера.

F=s₁²/s₂², F<F_крит

где Fкрит зависит от уровня значимости и числа степеней свободы для дисперсий в числителе и знаменателе.

В MS «MS Excel» для расчета уровня вероятности выполнения гипотезы о равенстве дисперсий могут быть использованы функция ФТЕСТ(массив1; массив2) и процеду­ра пакета анализа Двухвыборочный F-тест для дисперсий.

Непараметрические критерии. Непараметрические критерии используются в тех случаях, когда закон распределения данных отличается от нормального или неиз­вестен. Из большого числа непараметрических критериев рассмотрим критерий хи-квадрат.

Критерий согласия 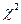- Бывают ситуации, когда необходимо сравнить две относи­тельные или выраженные в процентах величины (доли). Примером может слу­жить случай проверки успешности трудоустройства молодых специалистов, когда известен процент трудоустроившихся выпускников двух институтов. Для провер­ки достоверности различий здесь критерий Стьюдента применить не удастся. В та­ких задачах обычно используют критерий 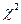(хи-квадрат). Критерий хи-квадрат относится к непараметрическим критериям.

Здесь, как и в случае с критерием Стьюдента, принимается нулевая гипотеза о том, что выборки принадлежат к одной генеральной совокупности. Кроме того, опреде­ляется ожидаемое значение результата. Обычно это среднее значение между вы­борками рассматриваемого показателя. Затем оценивается вероятность того, что ожидаемые значения и наблюдаемые принадлежат к одной генеральной совокуп­ности.

В MS «MS Excel» критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2-ТЕСТ вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют теоретическим (ожидаемым) значениям.

Функция имеет следующие параметры: ХИ2ТЕСТ(фактический_интервал; ожидаемый_интервал). Здесь:

О фактический^интервал − это интервал данных, которые содержат наблюде­ния, подлежащие сравнению с ожидаемыми значениями;

О ожидаемый_интервал − это интервал данных, который содержит теоретиче­ские (ожидаемые) значения для соответствующих наблюдаемых.

Пример 1.10. Пусть после окончания двух институтов экономического профиля трудоустроилось по специальности из первого института 90 человек, а из второго 60 (обе группы молодых специалистов включали по 100 человек).

Дата добавления: 2015-06-29