Решение. Рис. 1.13. Сопоставление выборочного распределения веса студенток и кривой нормального распределения

Вес

Рис. 1.13. Сопоставление выборочного распределения веса студенток и кривой нормального распределения

При большом числе наблюдений (n > 100) неплохие результаты дает вычисление выборочных параметров формы распределения: эксцесса и асимметрии (см. раз­делы «Использование специальных функций» и «Использование инструментов Пакета анализа»). Принято говорить, что предположение о нормальности распре­деления не противоречит имеющимся данным, если асимметрия близка к нулю, то есть лежит в диапазоне от -0,2 до 0,2, а эксцесс − от 2 до 4.

Наиболее убедительные результаты дает использование критериев согласия. Кри­териями согласия называют статистические критерии, предназначенные для про­верки согласия опытных данных и теоретической модели. Здесь нулевая гипотеза Н₀ представляет собой утверждение о том, что распределение генеральной сово­купности, из которой получена выборка, не отличается от нормального. Среди кри­териев согласия большое распространение получил непараметрический критерий 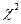(хи-квадрат). Он основан на сравнении эмпирических частот интервалов груп­пировки с теоретическими (ожидаемыми) частотами, рассчитанными по форму­лам нормального распределения.

Отметим, что сколько-нибудь уверенно о нормальности закона распределения можно судить, если имеется не менее 50 результатов наблюдений. В случаях мень­шего числа данных можно говорить только о том, что данные не противоречат нор­мальному закону, и в этом случае обычно используют графические методы оценки соответствия. При большем числе наблюдений целесообразно совместное исполь­зование графических и статистических (например, тест хи-квадрат или аналогич­ные) методов оценки, естественно дополняющих друг друга.

Использование критерия согласия хи-квадрат. Для применения критерия жела­тельно, чтобы объем выборки п > 40, выборочные данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а в каждом интервале находи­лось не менее 5 наблюдений (частот).

Отметим, что сравниваться должны именно абсолютные частоты, а не относитель­ные (частоты). При этом, как и любой другой статистический критерий, крите­рий хи-квадрат не доказывает справедливость нулевой гипотезы (соответствие эмпирического распределения нормальному), а лишь может позволить ее отверг­нуть с определенной вероятностью (уровнем значимости).

В MS «MS Excel» критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2-ТЕСТ вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют нормальному закону распределения. Если вычисленная вероятность близка к 1, то можно говорить о высокой степени соот­ветствия экспериментальных данных нормальному закону распределения.

Функция имеет следующие параметры:

ХИ2ТЕСТ (фактический_интервал;ожидаемый_интервал). Здесь:

О фактический_интервал − это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями;

О ожидаемый интервал − это интервал данных, который содержит теоретические (ожидаемые) значения для соответствующих наблюдаемых.

Пример 1.7. Проверить соответствие выборочных данных из примера 1.1. (64, 57, 63,62,58, 61, 63, 60, 60,61,65,62, 62, 60, 64, 61,59,59, 63,61, 62,58, 58, 63, 61, 59, 62, 60,60,58,61,60,63,63,58,60,59,60,59,61,62,62,63,57,61,58,60,64,60,59,61,64, 62, 59, 65) нормальному закону распределения.

1. Повторите пункты 1-7 решения примера 1.1. В результате получится таблица (см. рис. 1.2).

2. Найдите теоретические частоты нормального распределения. Для этого пред­варительно необходимо найти среднее значение и стандартное отклонение вы­борки.

В ячейке I13 с помощью функции СРЗНАЧ найдите среднее значение для данных из диапазона А2:Е12 (60,855). В ячейке J1З с помощью функции СТАНД0ТКЛ0Н най­дите стандартное отклонение для этих же данных (2,05). В ячейки К1 и К2 введите название столбца − Теоретические частости. Затем с помощью функции НОРМ-РАСП найдите теоретические частости. Установите курсор в ячейку К4, вызовите указанную функцию и заполните ее рабочие поля: х − G4; Среднее − $1$13; Стан-дартное_откл − $J$13; Интегральный − 0. Получим в ячейке К4 0,033. Далее протя­гиванием скопируйте содержимое ячейки К4 в диапазон ячеек К5:К12. Затем в ячей­ки L1 и L2 введите название нового столбца − Теоретические частоты. Установите курсор в ячейку L4 и введите формулу =Н$13*К4. Далее протягиванием скопи­руйте содержимое ячейки L4 в диапазон ячеек L5:L12. Результаты вычислений представлены на рис. 1.14.

G	H	I	J	K	L
Вес кг	Абсолютные частоты	Относи- тельные частоты	Накопленные частоты	Теоретические частости	Теоретические частоты
		0,036364	0,036364	0,033205828	1,82632055
		0,109091	0,145454909	0,073795567	4,058756212
		0,127273	0,272727636	0,129258576	7,109221655
		0,181818	0,454545818	0,178443849	9,814411704
		0,163636	0,618182182	0,194158732	10,67873029
		0,145455	0,763636727	0,16650428	9,157735407
		0,127273	0,890909455	0,112540024	6,189701326
		0,072727	0,963636727	0,059951732	3,297345259
		0,036364	1,000000364	0,025171529	1,384434082

Рис. 1.14. Результаты вычисления теоретических частостей и частот из примера 1.7

С помощью функции ХИ2ТЕСТ определите соответствие данных нормальному закону распределения. Для этого установите табличный курсор в свободную ячейку L13. На панели инструментов Стандартная нажмите кнопку Вставка функ­ции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ХИ2ТЕСТ, после чего нажмите кнопку ОК. Появившее­ся диалоговое окно ХИ2ТЕСТ отодвиньте вправо на 1-2 см от данных. Указате­лем мыши в рабочие поля введите фактический Н4:Н12 и ожидаемые L4:L12 ди­апазоны частот (рис. 1.15). Нажмите кнопку ОК. В ячейке L13 появится значение вероятности того, что выборочные данные соответствуют нормальному закону распределения − 0,9842.

Рис. 1.15. Пример заполнения рабочих полей функции ХИ2ТЕСТ

4. Поскольку полученная вероятность соответствия экспериментальных данных р = 0,98 много больше, чем уровень значимости 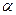= 0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат нормальному закону распределения. Более того, поскольку по­лученная вероятность р = 0,98 близка к 1, можно говорить о высокой степени вероятности того, что экспериментальные данные соответствуют нормально­му закону.

Дата добавления: 2015-06-29