Определение опорных реакций

Условие задания

Варианты и исходные данные домашнего задания № 4

На рис. 4.2, а изображена балка с четырьмя грузовыми участками, которая опирается на жёсткую заделку в т. 0и шарнирно-подвижную опору в т. 3. На рис. 4.2, б показаны типы внешних нагрузок и номера точек или участков их приложения. Вариант задания определяют по табл. 4.1 согласно шифру – двум последним цифрам зачётной книжки студента. Значения нагрузок и длин участков принимают из табл. 4.2 согласно второй цифре шифра.

а)
б)

Рис. 4.2. Схема опирания и нагружения балки

Таблица 4.1

Номера точек и участков приложения нагрузок

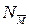
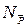
Цифры шифра	Пара сил	Сила	Распределённые нагрузки
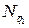
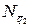
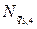
	а	б

а – первая цифра шифра; б – вторая цифра шифра.

Таблица 4.2

Значения нагрузок и длин грузовых участков

Вторая цифра шифра	,	,	,	,	,	,	,	,	,	,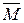
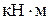
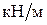
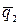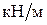
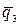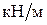
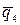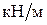
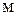
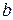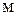
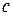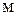
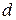		–10		–15		–10
	–21		–6		–12
		–12		–13		–14
	–23		–8		–16
		–14		–11		–18
	–25		–10		–18
		–16		–9		–16
	–27		–12		–14
		–18		–7		–12
	–29		–14		–10

Примечание. Знак “–” при числовых значениях нагрузок означает, что их направления необходимо показывать на схеме балки противоположно тем, которые изображены на рис. 4.1. б. В дальнейших расчётах значения нагрузок следует принимать по модулю, то есть положительными.

Для заданной схемы балки необходимо:

1. Определить опорные реакции.

2. Построить эпюры поперечных сил, изгибающих моментов и прогибов.

3. Подобрать сечение балки в виде стального прокатного двутавра из условий прочности и жесткости, если , .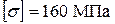

4. Произвести полную проверку правильности решения задачи.

4.3. Пример расчёта и методические указания

4.3.1. Подготовка исходных данных и расчётной схемы балки

Решение начинаем с выбора исходных данных из табл. 4.1 и 4.2. В качестве примера рассмотрим следующие данные. Номера точек и участков приложения нагрузок: 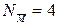; ; 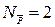– отсутствует; 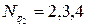; 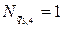. Значение нагрузок и длин грузовых участков: ; ; ; ; ; ; ; ; ; .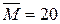

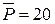
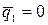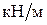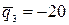
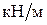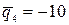
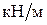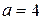
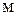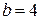
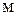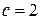
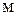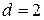
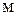Изображаем расчётную схему балки. Длину балки чертим в масштабе М 1:100 (в 1 см схемы – 1 м длины балки). Нагрузки 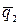, , 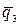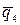направляем вниз (см. примечание к табл. 4.2). Для рассматриваемого примера расчётная схема балки показана на рис. 4.3, а.

Показываем реакции, возникающие в заделке 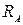, и шарнирно-подвижной опоре 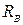(рис. 4.3, а). Очевидно, что двух уравнений равновесия, которые можно записать для системы параллельных сил (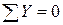; 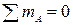), недостаточно для вычисления трёх неизвестных (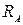, , 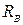). Следовательно, балка 1 раз статически неопределима:

n = R – U = 3 – 2 = 1.

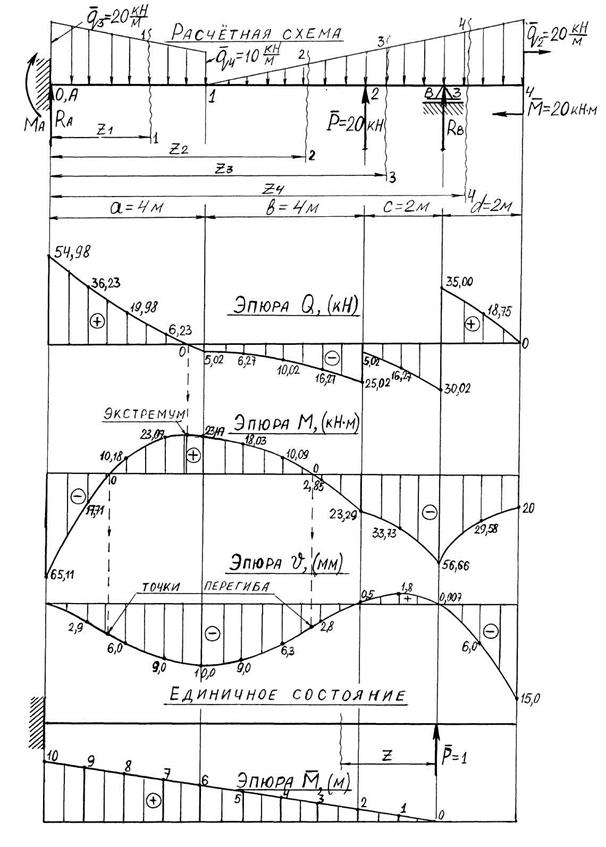
Для раскрытия неопределимости используем формулы метода начальных параметров для поперечной силы, изгибающего момента и прогиба (4.1). Учитывая специфику МНП (нумерация границ и правило знаков), выполним переприсвоение интенсивностей распределённых нагрузок, переходя от заданных обозначений к обозначениям МНП на основе расчётной схемы (рис. 4.3, а)

– слева от заделки (0-я граница) нагрузка отсутствует;

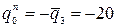
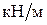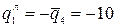
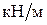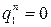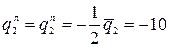
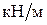; ; ; (средняя линия треугольника); 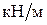(из подобия треугольников);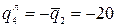 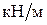; 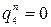– справа от 4-й границы нагрузка отсутствует.

а)
б)
в)
г)
д)
е)

Рис. 4.3. Расчётная схема балки. Эпюры Q, M,

Записываем и вычисляем все начальные и граничные параметры для k = 0, 1, 2, 3, используя расчётную схему (рис. 4.3, а) и формулы (4.2).

k = 0: 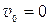– на опоре прогиб балки отсутствует; 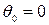– в глухой заделке угол поворота балки отсутствует; 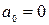– расстояние от левого края балки до 0-й границы; 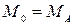– внешний момент равен неизвестному реактивному моменту в заделке; 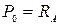– внешняя сила равна неизвестной опорной реакции в заделке;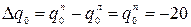 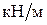– скачок распределённой нагрузки равен взятой с учётом знака интенсивности нагрузки справа от заделки; – слева от заделки нагрузка отсутствует; 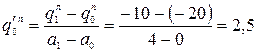– тангенс угла наклона трапецеидальной нагрузки; 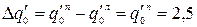– скачок тангенса угла наклона нагрузки равен взятому с учётом знака тангенсу угла наклона справа от заделки.

k = 1: ; ; ; ; ; ; .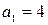

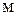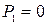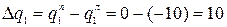
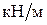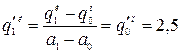
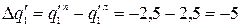
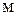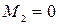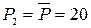
k = 2: ; ; ; 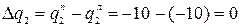–нагрузка не изменяет своей интенсивности; ; ; – нагрузка не изменяет своего наклона.

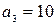
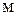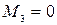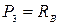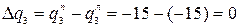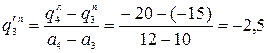
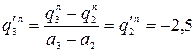
k = 3: ; ; ; –нагрузка не изменяет своей интенсивности; ; ; – нагрузка не изменяет своего наклона.

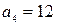
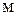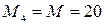
k = 4: ; ; 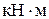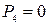. Остальные параметры не рассматриваем, так как справа от 4-й границы участок балки отсутствует.

Подставляем начальные и граничные параметры в формулы (4.1) и разворачиваем суммы по всем грузовым участкам. В результате получаем выражения поперечной силы, изгибающего момента и прогиба для рассматриваемого варианта балки:

;

;

.

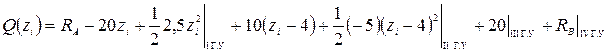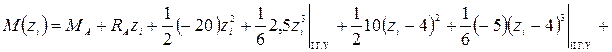
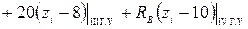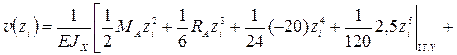
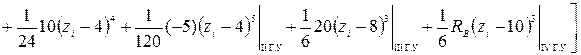Заметим, что действие формул для i -го грузового участка распространяется от знака равенства до вертикальной черты с индексом i Г.У.

В полученных функциональных зависимостях остаются неизвестными опорные реакции 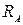, , 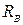. Чтобы их вычислить, составляем три уравнения, присваивая функциям 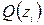, , 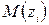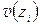те их значения, которые заведомо известны без вычислений. Согласно методу сечений на конце балки поперечная сила равна приложенной там сосредоточенной силе, взятой с учётом знака, а изгибающий момент равен приложенной там паре сил, также взятой с учётом знака. Кроме того, учтём, что прогиб балки над жёсткой опорой всегда равен нулю. Таким образом, можно записать, что

; ; ,

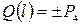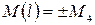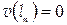где – длина балки; 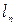– пролёт балки, равный расстоянию между опорами; – при вращении элемента балки по часовой стрелке; – при изгибе элемента балки выпуклостью вниз.

Для рассматриваемого варианта имеем

при ; ;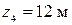

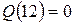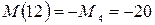
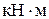при .

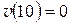Подставляя эти значения в выражения функци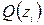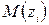й , и 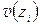, получаем

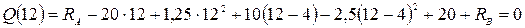или

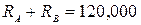; (4.3)

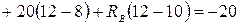или

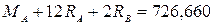; (4.4)

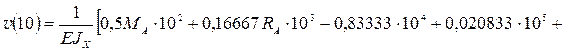
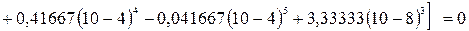или, умножая

на 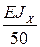, 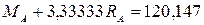. (4.5)

Объединяем уравнения (4.3) – (4.5) в систему и решаем её

; ; .

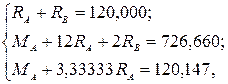
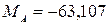
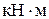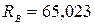
Проверяем правильность решения системы путём обратной подстановки в уравнения

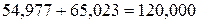– верно;

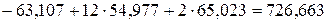≃726,660 – верно;

≃120,147 – верно.

Выполняем статическую проверку правильности определения реакций, записав два уравнения равновесия балки (рис. 4.3, а):

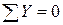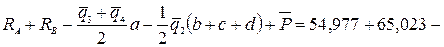
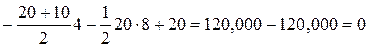; – выполняется;

;

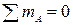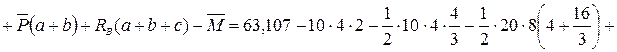
– выполняется.

Обратим внимание, что в данном примере трапецеидальная нагрузка 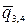при вычислении моментов разбилась на прямоугольную с интенсивностью 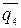и треугольную с максимальной интенсивностью 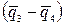. В случае разнозначной трапеции, когда 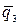и 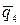имеют противоположные знаки, трапеция разбивается на два треугольника, равнодействующие которых направлены в разные стороны. Учитывая, что согласно табл. 4.2 модули интенсивностей нагрузок 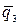и 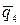отличаются в два раза, в таком же отношении будут находиться и протяжённости нагрузок или, другими словами, основания треугольников 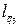и .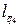

Дата добавления: 2015-06-30