Вычисление степени статической неопределимости

Условие задания

Варианты и исходные данные домашнего задания № 5

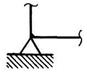
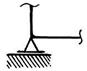
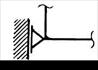
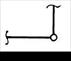
Конструкция плоской рамы состоит из шести прямолинейных элементов, соединённых между собой, как показано на рис. 5.4, а. Рама крепится к основанию с помощью различных видов внешних связей: глухой заделки, шарнирно-неподвижных и шарнирно-подвижных опор (рис. 5.4. б). Между собой стержни, как правило, сварены, но некоторые из них соединены внутренними шарнирами (рис. 5.4, б). Точки расположения опор и внутреннего шарнира указаны в табл. 5.1. Номер варианта соответствует порядковому номеру студента в журнале преподавателя.

а)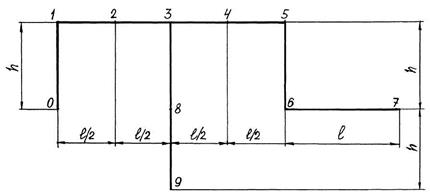
б)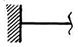
в)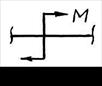

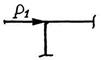
Рис. 5.4. Элементы расчётной схемы: а – геометрическая ось рамы;

б – виды опорных связей; в – внешние нагрузки

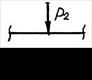
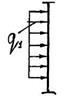
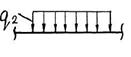
Рама нагружена внешними силовыми факторами, схематически показанными на рис. 5.4, в: парой сил с моментом М, горизонтальной 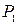и вертикальной 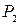сосредоточенными силами, горизонтальной 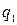и вертикальной 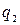распределёнными нагрузками. Места приложения внешних нагрузок (№ узлов и участков) указаны в табл. 5.2 и принимаются согласно шифру – двум последним цифрам номера зачётной книжки студента. Числовые данные внешних нагрузок и размеров рамы приведены в табл. 5.3, номер строки которой соответствует последней цифре шифра.

Для заданной согласно варианту и шифру схемы плоской рамы необходимо выполнить проектировочный расчёт на прочность: определить опорные реакции, построить эпюру изгибающих моментов, подобрать номер стального прокатного двутавра при 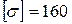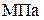и провести полную проверку правильности решения.

5.3. Пример расчёта и методические указания

5.3.1. Подготовка исходных данных и расчётной схемы

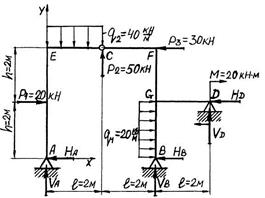
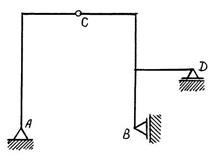
Решение задачи начинаем с выбора исходных данных из табл. 5.1 – 5.3. Затем вычерчиваем в масштабе М 1:100 расчётную схему рамы. Для рассматриваемого примера расчётная схема показана на рис. 5.5, а. Рама имеет три шарнирно-неподвижных опоры в т. A, B, D и внутренний шарнир в т. С. На схеме показываем характерные размеры и значения внешних нагрузок.

Показываем опорные реакции во всех внешних связях и подсчитываем их число 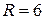(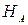; ; 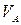; ; 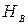; 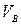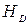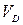). Находим общее число независимых уравнений равновесия 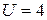(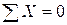; ; 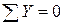; 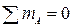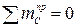). По формуле (5.1) вычисляем

.

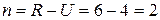Число замкнутых контуров 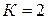(AEFBA; BGDB).

Число внешних и внутренних шарниров 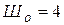(A; B; C; D).

Число шарнирно-подвижных катков .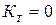

По формуле (5.2) вычисляем

.

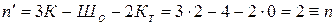Следовательно, заданная рама дважды статически неопределима.

Таблица 5.1

Кинематическая характеристика узлов рамы

№ варианта	№ точек расположения опор и внутреннего шарнира
Глухая заделка	Шарнирно- неподвижная опора	Горизонтальный каток	Вертикальный каток	Внутренний шарнир
			–
	–	7, 9		–	–
			–
	–	0, 9		–	–
			–
	–	0, 7		–	–
			–
	–	7, 9	–		–
			–
	–	0, 9	–		–
			–
	–	0, 7	–		–
				–
		–			–
				–
		–			–
				–
		–			–
				–
		–			–
				–
		–			–
				–
		–			–
	–	–	3, 6	0, 7, 9	–
	–	0, 7, 9	–	–
	–	0, 7
	–	0, 7, 9	–	–
	–			5, 9	–
	–			0, 5	–
	–			0, 7	–
	–			7, 9	–
	–		0, 5		–
	–			0, 5	–
	–	–		0, 5, 8, 9	–

Таблица 5.2

Активные нагрузки

Цифры шифра	№ узлов и участков
Момент пары сил М	Сосредоточенные силы	Распределённые нагрузки
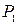
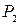
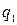
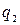
				5 – 6	1 – 2
				0 – 1	4 – 5
				3 – 9	2 – 3
				3 – 8	6 – 7
				0 – 1	3 – 4
				8 – 9	6 – 7
				5 – 6	4 – 5
				5 – 6	2 – 3
				0 – 1	6 – 7
				3 – 9	4 – 5
	а	б

а – первая цифра шифра; б – вторая цифра шифра.

Таблица 5.3

Статические и геометрические параметры

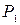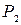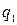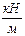
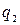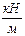
Цифра шифра	М,кН·м	, кН	, кН	,	,	l, м	h, м
	a

а)	б)
в)	г)
д)	е)
ж)	з)

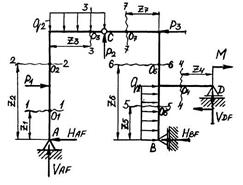
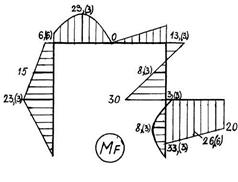
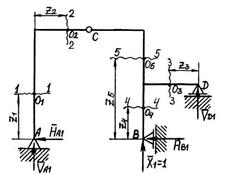
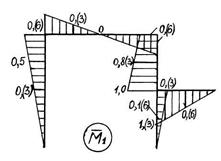
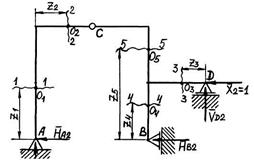
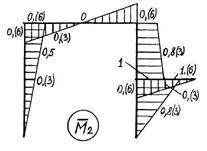
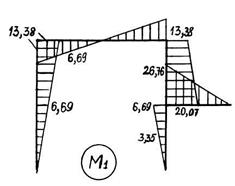
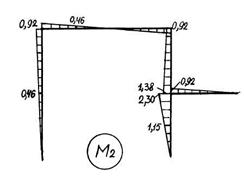
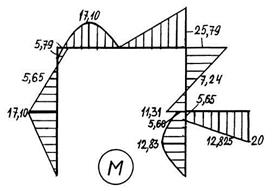
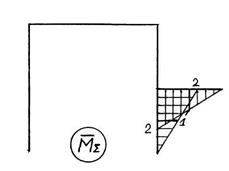
Рис. 5.5. Графическое оформление расчёта статически неопределимой рамы: а – заданная система; б – основная система; в – грузовое состояние основной системы; г – грузовая эпюра изгибающих моментов; д – I единичное состояние основной системы; е – I “единичная” эпюра изгибающих моментов; ж – II единичное состояние основной системы; з – II “единичная” эпюра изгибающих моментов; и – I исправленная эпюра изгибающих моментов; к – II исправленная эпюра изгибающих моментов; л – эпюра изгибающих моментов в заданной системе; м – суммарная “единичная” эпюра изгибающих моментов в основной системе

и)	к)
л)	м)

Рис. 5.5. Продолжение

Дата добавления: 2015-06-30