Методом сил

Рамой называется стержневая конструкция, состоящая из двух и более элементов, соединённых между собой и с основанием жёстко, шарнирно-неподвижно или шарнирно-подвижно (рис. 5.1). Такого рода конструкции нашли широкое распространение в машиностроении, в гражданском и промышленном строительстве, играя роль несущих каркасов машин, зданий и сооружений. По характеру восприятия элементами конструкций внешних нагрузок различают:

а) плоские рамы, когда все стержни и нагрузки расположены в одной плоскости;

б) плоско-пространственные рамы, когда силовая и конструктивная плоскости взаимно ортогональны (перпендикулярны);

в) пространственные рамы, когда стержни и нагрузки расположены произвольным образом.

Рамы бывают статически определимые и статически неопределимые. Рассмотрим класс плоских статически неопределимых рам, обобщающим показателем сложности расчёта которых является их степень статической неопределимости. На рис. 5.1 показан пример такой рамы.

B, E, D, H – жёсткое соединение дисков; A, F, I – шарнирно-неподвижное соединение дисков; C, G – шарнирно-подвижное соединение дисков.

Рис. 5.1. Плоская статически неопределимая рама

Степень статической неопределимости рамы можно вычислить на основе понятия этой величины по формуле

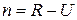, (5.1)

где R – число опорных реакций и линейно независимых от них внутренних усилий во всех стержнях рамы; U – общее число уравнений равновесия, которые можно составить для всей рамы в целом или отдельных её частей. Рассматриваемая рама (рис. 5.1) имеет восемь опорных реакций. Используя метод сечений, можно выразить внутренние усилия (N, Q, M) в любом элементе этой рамы через внешние нагрузки (M, P, q) и опорные реакции. Следовательно, .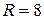

Общее число уравнений найдём следующим образом. Для всей рамы целиком можно составить три уравнения равновесия (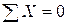, , 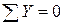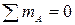); для части FHI можно составить одно дополнительное уравнение ( 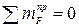– свойство шарнира); для части CD можно составить два дополнительных уравнения (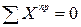, 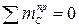– свойство катка). Таким образом, общее число уравнений равновесия 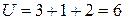, а степень статической неопределимости равна .

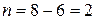Рассматриваемую величину можно вычислить также по синтезированной формуле

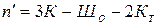, (5.2)

где К – число замкнутых контуров, образованных стержнями и основанием (опорным диском); 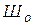– число простых шарниров (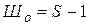, где S – число сходящихся в шарнире стержней); – число катковых (шарнирно-подвижных) соединений.

Для показанной на рис. 5.1 рамы получаем 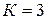(ABEGA; GFHIG; IHFECDI); 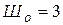(A; F; I); 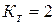(G; C). Следовательно,

.

Одним из самых распространённых методов раскрытия статической неопределимости является метод сил. В его основе лежит умение определять перемещения любых сечений рам от произвольных нагрузок. За неизвестные в этом методе принимают опорные реакции и (или) внутренние усилия в “лишних” внешних и (или) внутренних связях, безусловно не необходимых для обеспечения кинематической неизменяемости заданной рамы. Сущность метода сил заключается в следующем:

1. На основе статического и кинематического анализа вычисляют степень статической неопределимости по формулам (5.1) и (5.2).

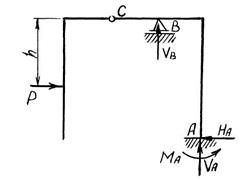
2. Выбирают так называемую основную систему метода сил путём отбрасывания n связей таким образом, чтобы оставшиеся U связей обеспечивали как статическую определимость, так и кинематическую (мгновенную) неизменяемость всей рамы и отдельных её частей. В принципе, основных систем можно выбрать несчётное множество. При выборе конкретного варианта обычно руководствуются: а) простотой и понятностью преобразования связей; б) наилучшим восприятием основной системой внешних нагрузок; в) авторским предпочтением тому или иному варианту. В любом случае, выбрав основную систему, необходимо провести её статический и кинематический анализ. Иногда случается так, что, выполнив формально отбрасывание n связей, получают механизм (рис. 5.2, а) или вырожденную систему (рис. 5.2, б), статическими признаками которых является противоречивость некоторых уравнений равновесия и невозможность вычисления реакций в отдельных опорных связях.

а)	б)
; ?! ; ? ?	; ?! ; ? ?

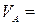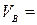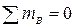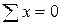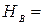Рис. 5.2. Псевдоосновные системы: а – механизм; б – вырожденная система

3. Рассматривают эквивалентную систему, получаемую путём загружения основной системы заданными внешними нагрузками 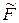и неизвестными реакциями, соответствующими отброшенным связям, которые обозначают буквами 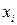(i = 1, 2, …, n). На основе адекватности заданной и эквивалентной систем получают канонические уравнения, выражающие равенства нулю перемещений по направлению отброшенных связей от всех приложенных силовых факторов,

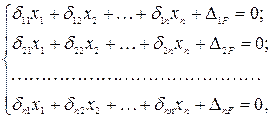(5.3)

где – податливость основной системы, имеющая смысл перемещения по направлению i -й отброшенной связи от действия силы 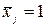, приложенной по направлению j -й отброшенной связи; 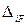– перемещение в основной системе по направлению i -й отброшенной связи от действия заданной внешней нагрузки 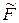. Указанные выше перемещения вычисляют согласно интегралу Мора перемножением “единичных” и грузовой эпюр внутренних усилий (изгибающих моментов) по правилу Верещагина и формуле Симпсона:

; , (5.4)

где EJ – изгибная жёсткость поперечных сечений стержней рамы; 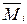и 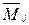– “единичные” эпюры изгибающих моментов в основной системе от действия сил и 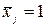; 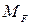– грузовая эпюра изгибающих моментов от действия нагрузки .

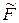Правило Верещагина применительно к одному грузовому участку рамы формулируется следующим образом: произведение двух эпюр, хотя бы одна из которых прямолинейна, равно площади криволинейной эпюры умноженной на ординату прямолинейной эпюры, взятую под центром тяжести криволинейной эпюры (рис. 5.3):

, (5.5)

где – площадь криволинейной эпюры; – ордината прямолинейной эпюры; – центр тяжести эпюры .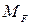

Формула Симпсона для одного грузового участка записывается в виде (рис. 5.3)

, (5.6)

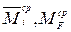где l – длина участка; – левые ординаты эпюр; – средние ординаты эпюр; 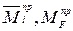– правые ординаты эпюр.

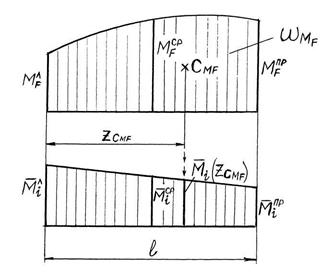
Рис. 5.3. Перемножение эпюр по правилу Верещагина и формуле Симпсона

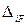4. После вычисления коэффициентов при неизвестных и свободных членов решают систему уравнений (5.3), в результате чего находят дополнительные неизвестные 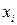. Основные неизвестные вычисляют, используя принцип суперпозиции. Например, горизонтальная реакция в опоре А заданной рамы

, (5.7)

где 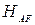– реакция в основной системе от внешней нагрузки; 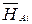– реакция в основной системе от единичной дополнительной неизвестной ; n – степень статической неопределимости заданной системы.

Аналогично находят характерные значения эпюры изгибающих моментов в заданной системе:

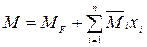. (5.8)

5. В заключение проводят проверочный или конструктивный расчёт на прочность, используя условие прочности при изгибе по нормальным напряжениям

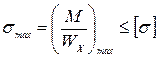, (5.9)

где М – расчётный изгибающий момент в наиболее опасном сечении рамы; 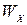– осевой момент сопротивления расчётного сечения; 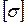– допускаемое напряжение при растяжении или сжатии.

Дата добавления: 2015-06-30