Изгиб стержней

Пример.

Для приведённой схемы нагружения прямого стержня (рис.46) построить эпюру крутящего момента при следующих исходных данных: m_z = 10 кН/м, L = 10 кНм,

l = 1 м.

Решение.

В соответствии со схемой нагружения запишем уравнение крутящего момента в следующем виде:

M_k (z) = M_k (0) │₁ - L│₂ - m_z(z-2l) │₃ .

Исходя из условий закрепления стержня, запишем следующее граничное условие: M_k (0) = 0 (реакция незакреплённого конца стержня равна нулю).

Рис.46

Таким образом, записанное уравнение не содержит неизвестных величин и можно приступать к построению графика. Построение графика будем производить аналогично построению графика в примере 1.

1 участок - 0 ≤ z ≤ l:

M_k (0) = 0 кНм,

M_k (l) = 0 кНм.

2 участок - l ≤ z ≤ 2l:

M_k (l) = 0 – 10 = -10 кНм,

M_k (2l) = 0 – 10 = -10 кНм.

3 участок - 2l ≤ z ≤ 3l:

M_k (2l) = 0 – 10 – 10(2 – 2) = - 10 кНм,

M_k (3l) = 0 – 10 – 10(3 – 2) = -20 кНм.

По рассчитанным значениям строится график крутящего момента (рис. 46).

Пусть стержень нагружен произвольной поперечной нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис.47). На данный элемент действует внешняя нагрузка и внутренние поперечные силы и изгибающие моменты в сечениях, по которым вырезан элемент.

Рис.47

Составим уравнения равновесия вырезанного элемента.

Уравнение равновесия всех сил на вертикальную ось.

- Q_y + q_y×dz + Q_y + dQ_y = 0,

,

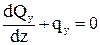Q_y’ + q_y = 0. (96)

Уравнение равновесия моментов относительно центра тяжести правого сечения вырезанного элемента.

- М_х + q_y×dz×dz/2 + М_х + dМ_х - Q_y×dz = 0,

слагаемое, выражающее момент от распределенной нагрузки, второго порядка малости, поэтому им можно пренебречь

,

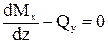М_х’ = Q_y. (97)

Объединяя дифференциальные уравнения (96) и (97), получим:

М_х'' = - q_y (98)

Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид

М_х(z) = C₁+С₂z – Ф_м,

где Ф_м – частное решение, отражающее внешнюю приложенную нагрузку.

Определим физический смысл постоянных интегрирования. При z=0

М_х(0) = C₁,

М_х’(0) = Q_y(0) = С₂.

Рассмотрим подробнее частное решение. Пусть стержень нагружен произвольной распределенной нагрузкой (рис.48). Определим величину поперечной силы и изгибающего момента для точки с координатой z.

Рис.48

Q_y = ,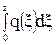

М_х = . (99)

Значения интегралов зависят от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенная сила (рис.49):

Рис.49

при z£a Ф_Q(z)=0

Ф_М(z)=0

при z³a Ф_Q(z)=-P

Ф_М(z)=-P(z-a)

б) распределенная нагрузка (рис.50):

Рис.50

при z£c Ф_Q(z)=0

Ф_М(z)=0

при z³c Ф_Q(z)=-q(z-c)

Ф_М(z)=-q(z-c)²/2

в) сосредоточенный момент (рис.51):

Рис.51

при z£b Ф_Q(z)=0

Ф_М(z)=0

при z³b Ф_Q(z)=0

Ф_М(z)=-L

Дата добавления: 2015-06-30