Сопротивление материалов 1 страница

Ч.3 - методическое пособие

по прикладной механике

Москва, 1012

УДК 621.81.001.66

Рекомендовано к изданию в качестве учебного пособия

редакционно-издательским советом МГУПИ

Рецензент: д.ф-м. наук, проф. Головешкин В.А.

кафедра «Прикладная механика» Московского

государственного университета приборостроения и информатики

В учебном пособии изложен материал по сопротивлению материалов, предназначенный для студентов, изучающих курсы «Сопротивление материалов», и «Прикладная механика» по кафедре «Прикладная механика».

Все разделы курса снабжены примерами и задачами.

Табл. Ил. Библиограф. 5 назв.

УДК: 531.8

Рекомендовано к изданию в качестве учебно-методического пособия редакционно-издательским советом МГУПИ

Рецензент

д.т.н., профессор В.А.Головешкин

Пирумов А.Р., Трофимова Г.Н., Холин Н.Н.

Сопротивление материалов: учебно-методическое пособие, 4.1. М.:МГУПИ, 2012, 120 с.

Для лучшего усвоения материала пособия мы рекомендуем студентам некоторые разделы теоретической механики, а для самостоятельной работы, кроме данного пособия, рекомендуются следующие учебники и пособия:

1. А.М. Кишкин, А.Р. Пирумов, Н.Н.Холин, Кинетика механической системы, ч. 2, М.: МГУПИ, 2011 г.
2. А.Р. Пирумов, Н.Н. Холин. Кинематика и кинетическая точка. Ч.1, М.,МГУПИ, 2011 г.
3. Федосьев В.И. Сопротивление материалов. 14 изд. Изд. МГТУ им Баумана, Москва, 2007 г.
4. Тимошенко О.П. Курс сопротивления материалов. 14 изд. Гос. издательство. Москва. 1930 г.
5. Л.И.Седов. Механика сплошной среды, «Наука», 1982, ч.2

Страница

Глава 1. Введение и основные понятия ………….……………………………………………………………..………..2

Глава 2. Напряжённо-деформированное состояние стержня при центральном растяжении (сжатии)……………....5

Глава 3. Учет собственного веса при растяжении и сжатии…………………………………………………………. 16

Глава 4. Напряжённое состояние в точке. Тензор напряжений………………………………………...……………..19

Глава 5. Плоское напряженное состояние……………………………………………………………………………....26

Глава 6. Упругое деформирование. Обобщённый закон Гука………………………….……………………………..31

Глава 7. Чистый изгиб балок…………………………………………………………………………………………….41

Глава 8. Поперечный изгиб балки. Формула Д.Журавского…………………………………………………………..48

Глава 9. Эпюры внутренних силовых факторов при изгибе…………,………………………………………………..56

Глава 10. Напряжения и деформации при кручении стержней кругового поперечного сечения……………………61

Глава 11. Расчета на сдвиг заклепочных соединений………………………….……………………………………….80

Глава 12. Устойчивость стержней………….……………………………………………………………………………83

Глава 13. Анализ формулы Эйлера……………………………………………………………………………………....90

Глава 14. Пределы применимости формулы Эйлера. Формула Ф.Ясинского…………………..…………………....93

Глава 15. Прочность при циклических нагрузках…………………..………………………………………………….101

Глава 16. Усталостная прочность………………………………………………………………………………………..106

Глава 17. Динамическое нагружение……………………………………………………………………………………111

Глава 1. Введение и основные понятия

Сопротивление материалов – наука о прочности, жесткости и устойчивости элементов инженерных конструкций. Методами сопротивления материалов ведутся прочностные расчеты и определяются необходимые размеры деталей машин, различных конструкций и сооружений.

Основные понятия сопротивления материалов опираются на законы и теоремы теории упругости, которая является разделом механики сплошной среды.

В отличие от теоретической механики сопротивление материалов рассматривает задачи, где наиболее существенными являются свойства деформируемых тел, а законы движения тела как абсолютно твёрдого являются несущественными.
Сопротивление материалов имеет целью создание инженерных методов расчета на прочность и устойчивость типичных, наиболее часто встречающихся элементов конструкций. Необходимость довести решение каждой практической задачи до некоторого числового результата заставляет прибегать к упрощающим гипотезам.

Определим основные понятия сопромата, которые мы использовали выше.

Прочность – способность конструкции выдерживать заданную нагрузку, не распадаясь на отдельные части.

Жесткость – это сопротивляемость тела деформированию.

Деформируемость – свойство конструкции изменять свои геометрические размеры и форму под действием внешних сил

Устойчивость – свойство конструкции сохранять при действии внешних сил исходную форму равновесия.

Механика сплошной среды рассматривает материал как сплошное тело, наделенное свойством однородности структуры. Материал обладает свойством упругости, то есть свойством тела восстанавливать свою форму после снятия внешних нагрузок.

Однородной называется структура, в которой механические свойства во всех точках тела одинаковы и не зависят от величины рассматриваемых объёмов.

Сплошность материала – это свойство заполнять все участки рассматриваемых объёмов. Это свойство вытекает из предыдущего.

Твёрдое тело мы называем изотропным, если в каждой точке его свойства по различным направлениям одинаковы. В действительности это часто не так. Например, свойства дерева вдоль волокон и поперёк волокон, свойства монокристаллов и т.д.

На рис. 1.1 представлены геометрические формы элементов конструкций, рассматриваемых в сопромате.

Рис.1.1 а) стержень, б) пластина, в) оболочка

Определим внешние нагрузки в зависимости от их величины, характера распределения (сосредоточенная или распределенная сила или момент), а также воздействия внешних полей и сред.

Внешние силы, действующие на элемент конструкции, подразделяются на 3 группы: 1) сосредоточенные силы, 2) распределенные силы, 3) объемные или массовые силы.

Сосредоточенные силы — силы, действующие на небольших участках поверхности конструкции.

Распределенные силы приложены к значительным участкам поверхности.

Объемные или массовые силы приложены к каждой частице материала (например силы тяжести, силы инерции).

Основным методом решения задач сопромата является «метод плоских сечений».

Метод плоских сечений состоит в следующем. Произвольно напряжённую конструкцию, например стержень, мысленно разделяем плоскостью на две части. Мысленно одна из частей тела отбрасывается. Для сохранения статического равновесия оставшейся части тела действие отброшенной части на оставшуюся заменяется действием внутренних сил взаимного сцепления. Начало координат помещается в центр тяжести плоскости сцепления. Внутренние силы взаимного сцепления приводятся к началу координат. Результирующими получаются главный вектор силы и главный вектор момента, которые раскладываются по осям координат. В результате получаем три силы и три момента, которые уже являются внешними силовыми факторами для рассматриваемой части тела и для стержня с продольной осью Z:

N(z) [H], [kH] – «нормальная» или «продольная» сила, обуславливает деформацию растяжения или сжатия.

Qx(z), Qy(z) – «поперечная» или «перерезывающая» сила, обуславливает деформацию сдвига.

Мх(z), My(z) [H m], [kH m] – «изгибающий момент», обуславливает деформацию изгиба.

Mz(z) – «крутящий момент» или «скручивающий момент», обуславливает деформацию кручения.

Основной гипотезой сопротивления материалов является гипотеза сечений Бернулли: «Сечения плоские до деформации остаются плоскими после деформации». В некоторых случаях, например, в задаче о кручении стержней некруглого поперечного сечения эта гипотеза неправомерна. Как следствие, методами сопротивления материалов решить такую задачу невозможно. В подобных случаях на помощь приходят науки с развитым математическим аппаратом, например, математическая теория упругости. С другой стороны, иногда с некоторыми допущениями удаётся использовать решения задач, когда гипотеза плоских сечений строго не соблюдается. Например, при определении нормальных напряжений в случае поперечного изгиба.

В сопротивлении материалов используются три принципа.

Первый принцип. Принцип независимости действия сил, или принцип суперпозиции: «Суммарный эффект от действия всех сил равен сумме эффектов от каждой силы в отдельности». Данный принцип основывается на законе Гука, где, например, существует линейная связь между напряжением (в формулировке принципа – это сила) и деформацией (в формулировке принципа – это эффект). Так при одновременном действии изгиба и растяжения суммарную деформацию в рассматриваемой точке тела получают простым сложением деформаций от изгиба и от растяжения.

Второй принцип. Принцип отвердения: «Под действием заданных нагрузок рассматриваемое тело в начале упруго деформируется, а затем отвердевает». Вследствие того, что абсолютные перемещения при упругом деформировании ничтожно малы по сравнению с размерами тела, то при составлении уравнений равновесия ими можно пренебречь и составлять уравнения для недеформированного состояния. Таким образом, этот принцип позволяет использовать уравнения статики для абсолютно твёрдого тела, которые неизмеримо проще уравнений, составляемых методами сопротивления материалов.

Третий принцип. Принцип Сен-Венана: «Распределение напряжений в сечениях достаточно удалённых от места приложения нагрузки не зависит от способа приложения нагрузки». Оказывается, что в областях приложения нагрузки способ приложения сказывается на характер распределения напряжений по сечению на длине, имеющей величину порядка величины поперечного сечения. Поэтому, исключив области приложения нагрузки, расчёты по определению напряжений можно проводить с помощью зависимостей, полученными методами сопротивления материалов. В областях приложения нагрузки расчёты ведутся по зависимостям для контактных напряжений, рассматриваемых в курсе деталей машин.

Замечание по поводу статически определимых и статически неопределимых систем.

Если при расчёте данной системы, находящейся в состоянии статического равновесия, все реакции в связях закрепления, а также внутренние усилия в её элементах можно определить только по методу плоских сечений, без использования дополнительных условий, то такая система называется статически определимой. На практике встречаются такие конструкции, при расчёте которых одних лишь уравнений равновесия оказывается недостаточно и требуется формулировка дополнительных уравнений, связанных с характером деформирования конструкций.

Системы, в которых количество положенных связей больше числа независимых уравнений равновесия называются статически неопределимыми.

Глава 2. Напряжённо-деформированное состояние стержня при центральном растяжении (сжатии).

1.Внутренние силовые факторы.

Y ℓ+∆ℓ

А а` а с с` В

P P

Z

b` b d d`

ℓ

Рис.2.1

Рассмотрим стрежень АВ, по торцам которого действуют силы Р, растягивающие его (рис.2.1).

Для установления вида напряженного состояния применим метод плоских сечений и определим внутренние силовые факторы (рис.2.2).

A

N(z) Z

Рис.2.2

Ограничимся рассмотрением случая, когда внешние силы Р приложены в центрах тяжестей торцевых сечений. Из рис.2.2 очевидно, что из всех внутренних силовых факторов отличной от нуля будет только нормальная сила N(z), приложенная в центре тяжести мысленного поперечного сечения. В этом случае имеет место так называемое центральное растяжение.

Условимся направлять нормальную силу по направлению внешней нормали. Составим уравнение равновесия:

- P + N(z)= 0

Откуда получаем: N(z)= P

Аналогично можно рассуждать в случае, когда пара сил Р сжимают стержень. В этом случае величину N(z) получим с отрицательным знаком.

Таким образом отличие растяжения и сжатия будет сказываться только в знаках. Знак плюс нормальной силы указывает на растяжение, знак минус – на сжатие.

2.Напряжения при растяжении – сжатии стержня.

Из определения понятий о напряжениях следует, что от действия нормальной силы возникают нормальные напряжения. При этом условимся, что по толщине стержня напряжения и деформации остаются неизменными. То есть, фактически можно ограничиться по определению напряжений по высоте поперечного сечения в плоскости поперечного сечения.

Закон распределения напряжений по сечению стержня можно представить различными способами: см. рис.2.3, 2.4 и 2.5

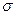
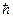
Z

N(z)

Рис.2.3

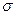
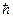
Z

N(z)

Рис.2.4

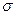
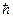
Z

N(z)

Рис.2.5

Примеры использования принципа Сен-Венана изображены на рис. 2.3 – 2.5. Принцип Сен-Венана позволяет получать приближённые решения задач теории упругости с помощью решения аналогичных задач для частных распределений действующих сил.

Введём понятия продольной деформации и продольного напряжения в соответствии с формулами (2.1) и (2.3). В сопротивлении материалов мы имеем дело с малыми упругими деформациями для которых справедлив закон Гука (см. 2.2).

Для установления закона распределения нормальных напряжений составим условие совместности деформации. Для этого воспользуемся гипотезой плоских сечений Бернулли.

Рассмотрим стержень постоянного поперечного сечения аb и cd.

ℓ(y)=const.

По гипотезе плоских сечений при растяжении эти сечения не искривятся и переместятся параллельно себе. В результате новое расстояние будет:

(ℓ+∆ℓ)(у)=const.

Абсолютное удлинение:

(ℓ+∆ℓ)(у)-ℓ(у)=∆ℓ(у)=const.

Относительное удлинение – деформация:

(2.1)

Используя закон Гука, связывающий напряжения с деформацией линейной зависимостью:

(2.2)

Где Е – модуль упругости (модуль Юнга).

Таким образом по сечению стержня нормальные напряжения распределяются равномерно (рис.2.5).

Согласно определению нормального напряжения

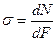(2.3)

Можем записать:

Так как , эту величину можно вынести из под знака интеграла:

То есть:

Откуда окончательно:

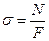(2.4)

При расчётах на жесткость при растяжении – сжатии требуется определять величину удлинения стержня под нагрузкой. Закон Гука можем записать следующим образом: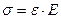

Подставляя значения напряжения и деформации, перепишем закон Гука:

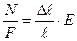где ℓ - длина стержня.

Отсюда выражение для удлинения ∆ℓ:

(2.5)

Таким образом, получили выражение для удлинения (укорочения) стержня при растяжении (сжатии). Жесткость стержня характеризуется произведением , которое так и называется «жесткость при растяжении – сжатии».

Расчеты на прочность при растяжении – сжатии.

Из формулы (2.4) следуют три рода задач, решаемые при растяжении – сжатии. Составляется уравнение прочности для наиболее опасного сечения:

где - допускаемое напряжение. (2.6)

Допускаемое напряжение определяется через механические характеристики материала.

- для пластичных материалов,

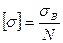- для хрупких материалов,

Где 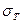- предел текучести,

- предел прочности, обе эти величины получают путем механических испытаний материала,

n – коэффициент запаса прочности, назначается в зависимости от рода материала, способа приложения нагрузки и степени ответственности детали.

Определение допускаемой нагрузки. Для расчётного «опасного» сечения определяется допускаемое значение внутреннего силового фактора:

В конкретных задачах существует однозначная связь величины с величиной внешней нагрузки. Таким образом, определяется величина допускаемой нагрузки.

Энергетический метод расчёта на прочность. Рассчитывается величина внутренней потенциальной энергии упругой деформации тела.

Внутренняя потенциальная энергия упругой деформации при растяжении – сжатии.

Энергия упругой деформации (U) подсчитывается в предположении, что нагрузка прикладывается статически. При этом работа внешних сил полностью переходит в потенциальную энергию упругой деформации. Процесс нагружения складывается следующим образом. При отсутствии нагрузки удлинение отсутствует. Чем больше нагрузка, тем больше удлинение стержня. Графически зависимость между статически прикладываемой нагрузкой и удлинением стержня можно представить в виде прямой в соответствии с законом Гука, см рис.2.6

P

0 ∆ℓ

Рис.2.6

Работа А определяется как площадь под кривой процесса:

Внутренняя энергия: U=A

Учитывая, что нормальная сила возникает от действия силы Р, можем записать:

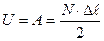
Подставляя из формулы (2.5) значение величины ∆ℓ, получим:

Для стержня, состоящего из n участков, окончательно получаем:

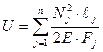
Удельная потенциальная энергия определяется как энергия, отнесённая к единице объёма V:

Где .

Удельную энергию можем определить следующим образом:

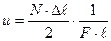
При этом: ; .

Энергетическая гипотеза прочности. Здесь «опасным» считается такое состояние, когда удельная потенциальная энергия элемента начнёт превышать допускаемое при простом центральном растяжении:

Пример.

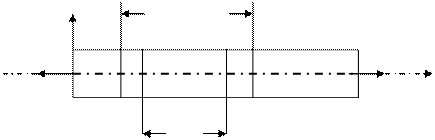
Стержень переменного сечения жестко защемлен в концевых сечениях и нагружен силой Р.

Требуется:

1) Определить реакции в заделках.

2) Построить эпюры нормальных сил N(z), нормальных напряжений 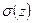, деформации 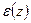и перемещений w(z). Для этого составить на каждом участке соответствующие аналитические выражения и определить в буквенном виде значения характерных ординат.

3) Определить из условия прочности допускаемую величину силы Р.

4) Определить энергию деформации двумя способами:

а) как работу внешних сил,

б) вычислить энергию деформации, используя аналитические выражения нормальных сил N(z).

Данные к задаче:

a =0.1м; ;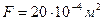

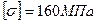
Примечания:

1) эпюра – это график исследуемой величины по оси стержня или по его поперечному сечению;

2) в нашем случае рассматривается задача когда напряжения и деформации по толщине стержня не меняются; и эпюры напряжений и деформаций строятся только по оси стержня.

Решение.

А В С 3 участок Д

Дата добавления: 2015-06-30