Сопротивление материалов 3 страница

Аналогичная подстановка в (5.1) приводит к выражению для нормальных напряжений на площадках с

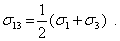(5.6)

Полученные соотношения позволяют проводить расчет конструкций на прочность в случае плоского напряженного состояния.

Глава 6. Упругое деформирование. Обобщённый закон Гука.

Действие внешних сил на твердое тело приводит к возникновению в точках его объема напряжений и деформаций. При этом напряженное состояние в точке, связь между напряжениями на различных площадках, проходящих через эту точку, определяются уравнениями статики и не зависят от физических свойств материала. Деформированное состояние, связь между перемещениями и деформациями устанавливаются с привлечением геометрических или кинематических соображений и также не зависят от свойств материала. Для того чтобы установить связь между напряжениями и деформациями, необходимо учитывать реальные свойства материала и условия нагружения. Математические модели, описывающие соотношения между напряжениями и деформациями, разрабатываются на основе экспериментальных данных. Эти модели должны с достаточной степенью точности отражать реальные свойства материалов и условия нагружения.

Наиболее распространенными для конструкционных материалов являются модели упругого тела. Упругость — это свойство тела изменять форму и размеры под действием внешних нагрузок и восстанавливать исходную конфигурацию при снятии нагрузок. Математически свойство упругости выражается в установлении взаимно однозначной функциональной зависимости между компонентами тензора напряжений и тензора деформаций. Свойство упругости отражает не только свойства материалов, но и условия нагружения. Для большинства конструкционных материалов свойство упругости проявляется при умеренных значениях внешних сил, приводящих к малым деформациям, и при малых скоростях нагружения, когда потери энергии за счет температурных эффектов пренебрежимо малы. Материал называется линейно-упругим, если компоненты тензора напряжений и тензора деформаций связаны линейными соотношениями (Закон Гука).

Пусть материал является линейно-упругим и изотропным. Рассмотрим элементарный объем, находящийся в условиях одноосного напряженного состояния (рис. 6.1), так что тензор напряжений имеет вид

При таком нагружении происходит увеличение размеров в направлении оси Ох, характеризуемое линейной деформацией 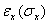, которая пропорциональна величине напряжения

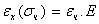
(6.1)

Рис. 6.1. Одноосное напряженное состояние

В гл. 2 отмечалось, что это соотношение является математической записью закона Гука, устанавливающего пропорциональную зависимость между напряжением и соответствующей линейной деформацией при одноосном напряженном состоянии. Коэффициент пропорциональности E называется модулем упругости или модулем Юнга. Он имеет размерность напряжений.

Наряду с увеличением размеров в направлении действия силы происходит уменьшение размеров в двух ортогональных направлениях (рис. 6.1). Соответствующие деформации обозначим через 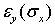и 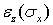, причем эти деформации отрицательны при положительных 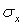и пропорциональны :

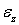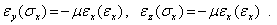
(6.2)

Коэффициент пропорциональности 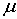называется коэффициентом Пуассона, который в силу изотропности материала одинаков для обоих ортогональных направлений.

Соотношения, аналогичные (6.1) и (6.2), в случае одноосного нагружения в направлении осей Y и X соответственно имеют вид

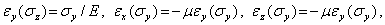
	(6.3)
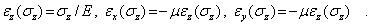
	(6.4)

При одновременном действии напряжений по трем ортогональным осям, когда отсутствуют касательные напряжения, для линейно-упругого материала справедлив принцип суперпозиции (наложения решений):

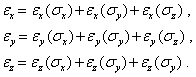
С учетом формул (6.1) – (6.4) получим

(6.5)

Касательные напряжения вызывают угловые деформации, причем при малых деформациях они не влияют на изменение линейных размеров, и следовательно, на линейные деформации. Поэтому они справедливы также в случае произвольного напряженного состояния и выражают так называемый обобщенный закон Гука.

Угловая деформация 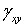обусловлена касательным напряжением 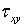, а деформаци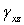и и 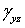— соответственно напряжениям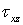и и 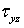. Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости

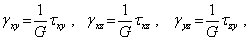
которые выражают закон Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига. Существенно, что нормальное напряжение не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними (рис. 6.1).

Линейная зависимость существует также между средним напряжением, пропорциональным первому инварианту тензора напряжений, и объемной деформацией, совпадающей с первым инвариантом тензора деформаций:

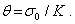
(6.6)

Рис. 6.2. Плоская деформация сдвига

Соответствующий коэффициент пропорциональности К называется объемным модулем упругости.

В формулы (6.1) – (6.6) входят упругие характеристики материала Е, 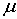, G и К, определяющие его упругие свойства. Однако эти характеристики не являются независимыми. Для изотропного материала независимыми упругими характеристиками являются две, в качестве которых обычно выбираются модуль упругости Е и коэффициент Пуассона 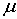. Чтобы выразить модуль сдвига G через Е и 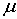, рассмотрим плоскую деформацию сдвига под действием касательных напряжений 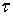(рис. 6.2). Для упрощения выкладок используем квадратный элемент со стороной а. Вычислим главные напряжения 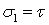, 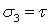. Эти напряжения действуют на площадках, расположенных под углом 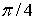к исходным площадкам. Из рис. 6.2 найдем связь между линейной деформацией 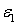в направлении действия напряжения 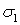и угловой деформацией 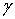. Большая диагональ ромба, характеризующая деформацию 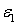, равна

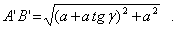
Для малых деформаций

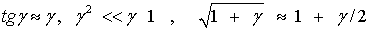
С учетом этих соотношений

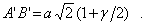
До деформации эта диагональ имела размер . Тогда будем иметь

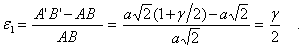
Из обобщенного закона Гука (6.5) получим

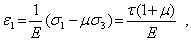
откуда

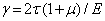
Сравнение полученной формулы с записью закона Гука при сдвиге дает

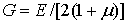
Сложим три соотношения упругости (6.5)

(6.7)

В итоге получим

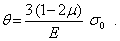
Сравнивая это выражение с объемным законом Гука (6.6), приходим к результату

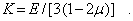
Механические характеристики Е, 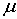, G и К находятся после обработки экспериментальных данных испытаний образцов на различные виды нагрузок. Из физического смысла все эти характеристики не могут быть отрицательными. Кроме того, из последнего выражения следует, что коэффициент Пуассона для изотропного материала не превышает значения 1/2. Таким образом, получаем следующие ограничения для упругих постоянных изотропного материала:

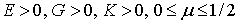
Предельное значение 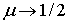приводит к предельному значению 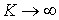, что соответствует несжимаемому материалу. Выразим из соотношений упругости напряжения через деформации. Запишем первое из соотношений (6.5) в виде

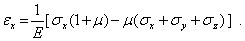
С использованием равенства (6.7) будем иметь

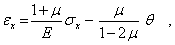
откуда

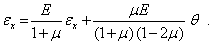
Аналогичные соотношения можно вывести для 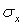и . В результате получим

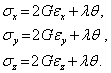
(6.8)

Здесь использовано соотношение для модуля сдвига. Кроме того, введено обозначение

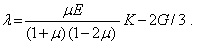
ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ

Рассмотрим вначале элементарный объем dV=dxdydz в условиях одноосного напряженного состояния (рис. 6.1). Мысленно закрепим площадку х=0. На противоположную площадку действует сила 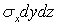. Эта сила совершает работу на перемещении 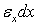. При увеличении напряжения от нулевого уровня до значения 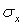соответствующая деформация в силу закона Гука также увеличивается от нуля до значения 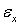, а работа пропорциональна заштрихованной на рис. 4 площади: 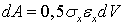. Если пренебречь кинетической энергией и потерями, связанными с тепловыми, электромагнитными и другими явлениями, то в силу закона сохранения энергии совершаемая работа перейдет в потенциальную энергию, накапливаемую в процессе деформирования: 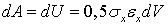. Величина Ф= dU / dV называется удельной потенциальной энергией деформации, имеющей смысл потенциальной энергии, накопленной в единице объема тела. В случае одноосного напряженного состояния

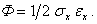
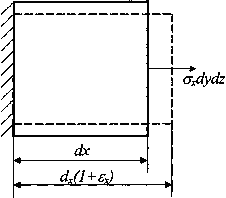
Рис. 6.3. Расчетная схема энергии деформации

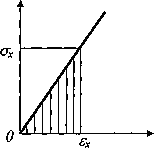
Рис. 6.4. Линейный закон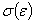

При одновременном действии напряжени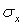й , и 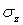на главных площадках (т. е. при отсутствии касательных напряжений) потенциальная энергия равна сумме работ, совершаемых силами 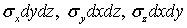на соответствующих перемещениях 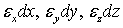. Удельная потенциальная энергия равна

.

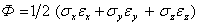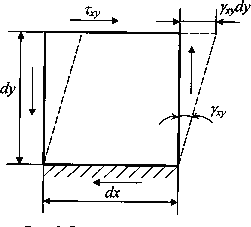
Рис. 6.5. Расчетная схема энергии сдвига

В частном случае чистого сдвига в плоскости Оху, изображенном на рис. 5, сила 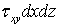совершает работу на перемещении 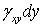. Соответствующая этому случаю удельная потенциальная энергия деформации равна

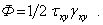
Подобные соотношения будут иметь место при сдвиге в других плоскостях.

В общем случае напряженно-деформированного состояния будем иметь

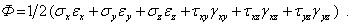
(6.9)

Если деформации выразить через напряжения с помощью соотношений упругости, то получим эквивалентную форму записи через компоненты тензора напряжений

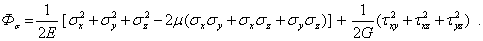
(6.10)

Выразив напряжения через деформации с использованием закона Гука, получим еще одну форму записи для Ф — через компоненты тензора деформаций

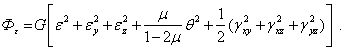
Глава 7. Чистый изгиб балок.

Стержни, работающие на изгиб, в технике получили название «балка».

Далее мы будем рассматривать только прямой изгиб балок, когда на поверхности балки действуют силы перпендикулярные её оси в главной плоскости, проходящей через продольную ось стержня и одну из главных осей инерции сечения.

При чистом изгибе балки в поперечном сечении стержня возникает только один силовой фактор — изгибающий момент М_х (рис. 7.1). Так как Q_y=dM_x/dz=0, то M_x =const и чистый прямой изгиб может быть реализован при загружении стержня парами сил, приложенными в торцевых сечениях стержня. Поскольку изгибающий момент M_х по определению равен сумме моментов внутренних сил относительно оси Ох с нормальными напряжениями его связывает выкающее из этого определения уравнение статики

.

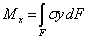Проанализируем деформации балки из низкомодульного материала, на боковой поверхности которой нанесена сетка продольных и поперечных рисок (рис. 7.2). Поскольку поперечные риски при изгибе стержня парами сил, приложенными в торцевых сечениях, остаются прямыми и перпендикулярными к искривленным продольным рискам, это позволяет сделать вывод о выполнении гипотезы плоских сечении. Точное решение этой задачи методами теории упругости, перестает быть гипотезой и становится точным фактом. Замеряя изменение расстояний между продольными рисками, приходим к выводу о справедливости гипотезы о ненадавливании продольных волокон .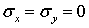

Ортогональность продольных и поперечных рисок до и после деформирования (как отражение действия закона плоских сечений) указывает также на отсутствие сдвигов, касательных напряжений в поперечных и продольных сечениях стержня.

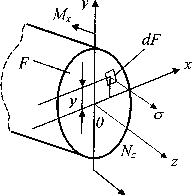
Рис. 7.1. Связь внутреннего усилия и напряжения

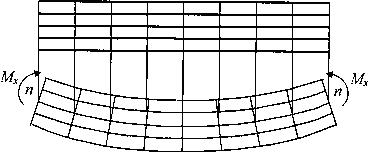
Рис. 7.2. Модель чистого изгиба

Таким образом, чистый изгиб призматической балки сводится к одноосному растяжению или сжатию продольных волокон напряжениями 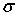(индекс г в дальнейшем опускаем). При этом часть волокон находится в зоне растяжения (на рис. 2 это—нижние волокна), а другая часть—в зоне сжатия (верхние волокна). Эти зоны разделены нейтральным слоем (п—п), не меняющим своей длины, напряжения в котором равны нулю. Учитывая сформулированные выше предпосылки и полагая, что материал стержня линейно-упругий, подчиняется закону Гука 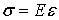, выведем формулы для кривизны нейтрального слоя 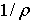( 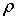—радиус кривизны) и нормальных напряжений 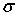. Предварительно отметим, что постоянство поперечного сечения призматического стержня и изгибающего момента (M_х=сonst), обеспечивает постоянство радиуса кривизны нейтрального слоя по длине стержня (рис. 7.3, а), нейтральный слой (п—п) описывается дугой окружности.

Рассмотрим призматическую балку в условиях чистого изгиба (рис. 7.3, а) с поперечным сечением, симметричным относительно вертикальной оси Оу. Это условие не отразится на конечном результате (чтобы прямой изгиб был возможен, необходимо совпадение оси Оу с главной осью инерции поперечного сечения, которая и является осью симметрии). Ось Ox поместим на нейтральном слое, положение которого заранее неизвестно.

а) расчетная схема, б) деформации и напряжения

Рис. 7.3. Фрагмент чистого изгиба бруса

Рассмотрим вырезанный из стержня элемент длиной dz, который в масштабе с искаженными в интересах наглядности пропорциями изображен на рис. 7.3, б. Поскольку интерес представляют деформации элемента, определяемые относительным смещением его точек, одно из торцевых сечений элемента можно считать неподвижным. Ввиду малости 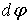считаем, что точки поперечного сечения при повороте на этот угол перемещаются не по дугам, а по соответствующим касательным.

Вычислим относительную деформацию продольного волокна АВ, отстоящего от нейтрального слоя на у:

.

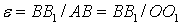Из подобия треугольников С00₁ и 0₁ВВ₁ следует, что

.

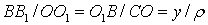Продольная деформация 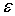оказалась линейной функцией расстояния от нейтрального слоя, что является прямым следствием закона плоских сечений

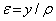
(7.1)

Тогда нормальное напряжение, растягивающее волокно АВ, на основании закона Гука будет равно

(7.2)

Эта формула не пригодна для практического использования, так как содержит две неизвестные: кривизну нейтрального слоя 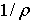и положение нейтральной оси Ох, от которой отсчитывается координата у. Для определения этих неизвестных воспользуемся уравнениями равновесия статики. Первое выражает требование равенства нулю продольной силы

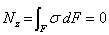
(7.3)

Подставляя в это уравнение выражение (7.2)

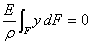
и учитывая, что 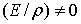, получаем, что

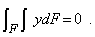
Интеграл в левой части этого уравнения представляет собой статический момент поперечного сечения стержня относительно нейтральной оси Ох, который может быть равным нулю только относительно центральной оси. Поэтому нейтральная ось Ох проходит через центр тяжести поперечного сечения.

Второе уравнение равновесия статики связывает нормальные напряжения с изгибающим моментом, который легко может быть выражен через внешние силы и поэтому считается заданной величиной. Подставляя выражение для. напряжений в уравнение (7.3):

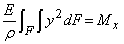
и учитывая, что 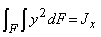где J_x —главный центральный момент инерции относительно оси Ох, для кривизны нейтрального слоя получаем формулу

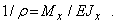Для малых прогибов балки можно принять: y= Mx / EJx (см. гл. 12)

(7.4)

Кривизна нейтрального слоя является мерой деформации стержня при чистом изгибе. Она тем меньше, чем больше величина EJ_х, называемая жесткостью поперечного сечения при изгибе (по аналогии с жесткостью поперечного сечения при растяжении EF).

Подставляя (7.4) в (7.2), получаем формулу для нормальных напряжений в виде

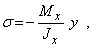
(7.5)

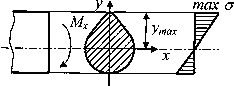
Рис. 7.4. Распределение нормальных напряжений

Для согласования знаков изгибающего момента М_х и нормальных напряжений 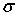в правой части формулы (7.5) ставится знак минус, так как при M_х>0 нормальные напряжения 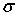при y >0 оказываются сжимающими. Однако в практических расчетах удобнее, не придерживаясь формального правила знаков, определять напряжения по модулю, а знак ставить по смыслу. Нормальные напряжения при чистом изгибе призматического стержня являются линейной функцией координаты у и достигают наибольших значений в волокнах, наиболее удаленных от нейтральной оси (рис. 4), т. е.

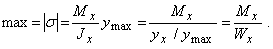
Здесь введена геометрическая характеристика 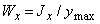, имеющая размерность м³ и получившая название момента сопротивления при изгибе. Поскольку при заданном M_х напряжения тем меньше, чем больше W_x, момент сопротивления является геометрической характеристикой прочности поперечного сечения при изгибе. Приведем примеры вычисления моментов сопротивления для простейших форм поперечных сечений. Для прямоугольного поперечного сечения имеем J_х=bh³/12,y_max = h/2 и W_x = J_x/y_max = bh²/6. Аналогично для круга (рис. 7 ,a J_x = 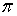d⁴ /64, y_max=d/2) получаем W_x = 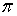d³ /32, для кругового кольцевого сечения, у которого

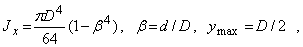
получаем

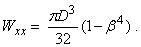
Итак, максимальные нормальные напряжения в сечении с изгибающим моментом M_х определяются по формуле

(7.6)

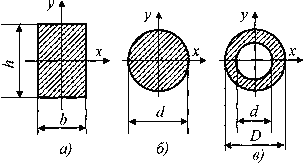
Рис. 7.5. Конфигурации поперечных сечений бруса

Этой формулой удобно пользоваться для расчета балок пластичного материала в упругой области, одинаково работающего на растяжение и сжатие. Поскольку знак напряжения в этом случае не имеет значения, напряжения вычисляются по модулю, и условие прочности при изгибе балки в форме призматического стержня получает вид

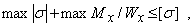
где max M_х— максимальное значение изгибающего момента (легко определяемое по его эпюре), 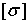— допускаемое напряжение на простое растяжение (сжатие). Напомним, что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором ).

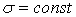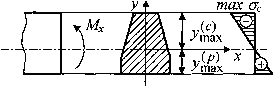
Рис. 7.6. Модель изгиба хрупкого материала

При расчете балок из хрупких материалов следует различать наибольшие растягивающие max 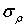и наибольшие сжимающие 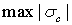напряжения (рис. 6.), которые также определяются по модулю непосредственно и сравниваются с допускаемыми напряжениями на растяжение 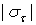и сжатие 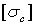. Условие прочности в этом случае будет иметь вид:

.

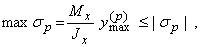
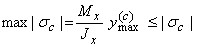Глава 8. Поперечный изгиб балки. Формула Д. Журавского.

При поперечном изгибе в сечениях стержня возникает изгибающий момент М_х и поперечная сила Q_y (рис. 8.1), которые связаны с нормальными 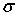и касательными 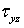напряжениями

Дата добавления: 2015-06-30