Сопротивление материалов 2 страница

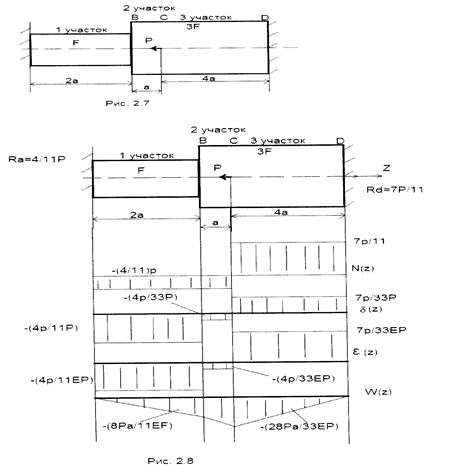
1 участок 3F

F P Z

2a a 4a

Рис.2.7

Обозначаем характерные сечения начальными буквами латинского алфавита. Проводим продольную ось Z. см.рис.2.7. Отбрасываем мысленно заделку и заменяем на действия реакциями R_A и R_Д, направляя обе в стороны, противоположные направлению силы Р. Удобно на этой схеме провести оси будущих эпюр.

Составляем уравнение равновесия: 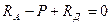, R_A+R_Д=P

Остальные уравнения равновесия дают тождественный ноль.

Таким образом, получаем одно уравнение с двумя неизвестными. Для решения поставленной задачи не достаёт одного уравнения, значит задача один раз статически неопределимая. Составим уравнения совместности перемещений, воспользовавшись законом Гука и принципом независимости действия сил.

Мысленно отбросим связь заделки в сечении А, заменив её действие силой R_A. При этом опора D сохраняется. Перемещение сечения А к сечению D под действием силы R_A будет равно:

При этом, жёсткость на 2 и 3 участках одинаковы, поэтому для 2 и 3 участков составляется общее слагаемое. Далее сечение освободим от нагрузки. Тогда перемещение сечения С к сечению D будет равно:

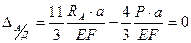
После простейших арифметических действий получаем:

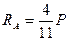
Данный класс задач удобнее решать в простых дробях, что позволяет получать конечный результат в абсолютном значении без всяких приближений.

Аналогичные рассуждения в отношении правой реакции опоры приводят к результату

R д =7/11 P

Легко проверить, что при этом уравнение равновесия выполняется.

Построение эпюр.

Принято строить эпюры на недеформированном стержне.

Участок АВ. Мысленно делим стержень на 2 части и отбрасываем правую часть. Рассматриваем равновесие левой части. Мысленно направляем нормальную силу по внешней нормали и записываем уравнение равновесия левой части:

N(Z1) + Ra = 0;

То же отсечение левой части проводим на участке ВС, для которого условие равновесия имеет такой же вид, как и для

участка АВ. Таким образом нормальная сила на участках АВ и СD одинакова по величине и направлению (сжатие).

На участке CD стержень испытывает растяжение, так как из уравнения равновесия левой части стержня (при сечении

участка CD) следует:

N(Z3) = P – Ra > 0

Используя определение (2.4) для каждого из трёх участков определяем нормальные напряжения и строим

эпюру. Из закона Гука (2.2) определяем значения деформаций.

Строим эпюру нормальной силы

Эпюра перемещений W(Z).

Так как в пределах каждого участка деформации постоянны, то для построения эп.ры перемещений достаточно определить значения перемещений на границах участков и соединить эти координаты прямыми.

В сечении А перемещение отсутствует:

W(A)=0

В сечении В перемещение определяется деформацией первого участка:

и т.д.

Глава 3. Учет собственного веса при растяжении и сжатии.

Пусть вертикальный стержень (Рис.3.1) закреплен своим верхним концом; к нижнему его концу подвешен груз Р. Длина стержня l, площадь поперечного сечения F, удельный вес материала 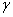и модуль упругости Е. Подсчитаем напряжения по сечению АВ, расположенному на расстоянии от свободного конца стержня.

а) б)

Рис. 3.1. Исходная расчетная схема бруса а) и б) — равновесие нижней отсеченной части.

Рассечем стержень сечением АВ и выделим нижнюю часть длиной с приложенными к ней внешними силами (Рис.1, б) — грузом Р и ее собственным весом 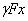. Эти две силы уравновешиваются напряжениями, действующими на площадь АВ от отброшенной части. Эти напряжения будут нормальными, равномерно распределенными по сечению и направленными наружу от рассматриваемой части стержня, т. е. растягивающими. Величина их будет равна:

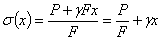
Таким образом, при учете собственного веса нормальные напряжения оказываются неодинаковыми во всех сечениях. Наиболее напряженным, опасным, будет верхнее сечение, для которого достигает наибольшего значения l; напряжение в нем равно:

Условие прочности должно быть выполнено именно для этого сечения:

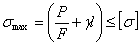
Отсюда необходимая площадь стержня равна:

От формулы, определяющей площадь растянутого стержня без учета влияния собственного веса, эта формула отличается лишь тем, что из допускаемого напряжения вычитается величина .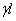

Чтобы оценить значение этой поправки, подсчитаем ее для двух случаев. Возьмем стержень из мягкой стали длиной 10 м; для него 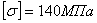, а величина . Таким образом, для стержня из мягкой стали поправка составит т. е. около 0,6%. Теперь возьмем кирпичный столб высотой тоже 10 м; для него , а величина Таким образом, для кирпичного столба поправка составит , т.е. уже 15%.

Понятно, что влиянием собственного веса при растяжении и сжатии стержней можно пренебрегать, если мы не имеем дела с длинными стержнями или со стержнями из материала, обладающего сравнительно небольшой прочностью (камень, кирпич) при достаточном весе. При расчете длинных канатов подъемников, различного рода длинных штанг и высоких каменных сооружений (башни маяков, опоры мостовых ферм) приходится вводить в расчет и собственный вес конструкции.

В таких случаях возникает вопрос о целесообразной форме стержня. Если мы подберем сечение стержня так, что дадим одну и ту же площадь поперечного сечения по всей длине, то материал стержня будет плохо использован; нормальное напряжение в нем дойдет до допускаемого лишь в одном верхнем сечении; во всех прочих сечениях мы будем иметь запас в напряжениях, т. е. излишний материал. Поэтому желательно так спроектировать размеры стержня, чтобы во всех его поперечных сечениях (перпендикулярных к оси) нормальные напряжения были постоянны,

Такой стержень называется стержнем равного сопротивления растяжению или сжатию. Если при этом напряжения равны допускаемым, то такой стержень будет иметь наименьший вес.

При определении влияния собственного веса на деформацию при растяжении и сжатии стержней придется учесть, что относительное удлинение различных участков стержня будет переменным, как и напряжение 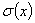. Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка стержня длиной 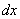, находящегося на расстоянии от конца стержня (Рис. 3.1).

Абсолютное удлинение этого участка равно

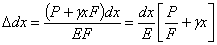
Полное удлинение стержня 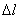равно:

Величина представляет собой полный вес стержня. Таким образом, для вычисления удлинения от действия груза и собственного веса можно воспользоваться прежней формулой:

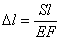
подразумевая под S внешнюю силу и половину собственного веса стержня.

Что же касается деформаций стержней равного сопротивления, то, так как нормальные напряжения во всех сечениях одинаковы и равны допускаемым 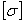, относительное удлинение по всей длине стержня одинаково и равно

Абсолютное же удлинение при длине стержня l равно:

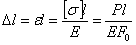
где обозначения соответствуют приведенным на рис. 3.1.

Деформацию ступенчатых стержней следует определять по частям, выполняя подсчеты по отдельным призматическим участкам. При определении деформации каждого участка учитывается не только его собственный вес, но и вес тех участков, которые влияют на его деформацию, добавляясь к внешней силе. Полная деформация получится суммированием деформаций отдельных участков.

Глава 4. Напряжённое состояние в точке. Тензор напряжений.

Вектор напряжений p_n является физическим объектом, имеющим длину, направление и точку приложения. В этом смысле он обладает векторными свойствами. Однако этому объекту присущи некоторые свойства, не характерные для векторов. В частности, величина и направление вектора напряжений зависят от ориентации вектора n нормали бесконечно малого элемента поверхности dF. Совокупность всех возможных пар векторов п, р_n в точке определяет напряженное состояние в данной точке. Однако для полного описания напряженного состояния в точке нет необходимости задавать бесконечное множество направлений вектора n, достаточно определить векторы напряжений на трех взаимно перпендикулярных элементарных площадках. Напряжения на произвольно ориентированных площадках могут быть выражены через эти три вектора напряжений. Так, что ось Z – продольная ось бруса, а X и Y – координаты любой точки его поперечного сечения.

Проведем через точку М три взаимно перпендикулярных плоскости с векторами нормалей, направления которых совпадают с направлениями координатных осей. Элементарные площадки образуем дополнительными сечениями, параллельными исходным плоскостям и отстоящими от них на бесконечно малые расстояния dx, dy, dz. В результате в окрестности точки М получим бесконечно малый параллелепипед, поверхность которого образована элементарными площадками dF_х=dydz, dF_н==dxdz, dF_я=dxdy.

Разложим каждый вектор напряжений на составляющие вдоль координатных осей (рис. 4.1). На каждой площадке действует одно нормальное напряжение 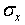, , , 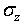где индекс обозначает направление вектора нормали к площадке и два касательных напряжения 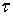с двумя индексами, из которых первый указывает направление действия компоненты напряжения, второй—направление вектора нормали к площадке.

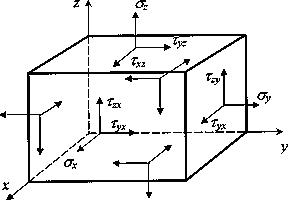
Рис.4.1. Компоненты тензора напряженного состояния

Совокупность девяти компонент напряжений (по три на каждой из трех взаимно перпендикулярных площадок) представляет собой объект, называемый тензором напряжений в точке. Тензор можно представить в виде матрицы:

Для компонент тензора напряжений общепринятым является следующее правило знаков: компонента считается положительной, если на площадке с положительной внешней нормалью (т. е. направленной вдоль одной из координатных осей) эта компонента направлена в сторону положительного направления соответствующей оси. На рис. 4.1 все компоненты тензора напряжений изображены положительными. На площадках с отрицательной внешней нормалью (грани параллелепипеда, не видимые на рис. 4.1) положительная компонента направлена в противоположном направлении. Напряжения на трех взаимно ортогональных площадках с отрицательными направлениями нормалей также характеризуют напряженное состояние в точке. Эти напряжения, являющиеся компонентами тензора напряжений, определяются аналогично напряжениям на площадках с положительной нормалью.

Тензор напряжений обладает свойством симметрии. Для доказательства этого свойства рассмотрим элементарный параллелепипед с действующими на его площадках компонентами тензора напряжений. Так как тело находится в равновесии, следовательно, находится в равновесии любая его часть, в том числе и элементарный объем. Запишем одно из шести уравнений равновесия этого объема, а именно — сумму моментов всех сил относительно оси Ох. Все силы, кроме двух, либо не создают момента относительно ocи Ох, либо взаимно уничтожаются. Отличные от нуля моменты создают компоненты 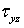(верхняя грань) и (правая грань):

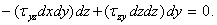
Откуда следует:

Аналогично, приравнивая нулю сумму моментов всех сил относительно осей Оу и Ог, получим еще два соотношения

Эти условия симметрии тензора напряжений называются также условиями парности касательных напряжений: касательные напряжения, действующие по двум взаимно перпендикулярным площадкам в направлениях, ортогональных ребру, образованному пересечением этих площадок, равны по величине. С учетом этих свойств из девяти компонент тензора напряжений независимыми оказываются шесть компонент.

Покажем теперь, что компоненты тензора напряжений определенные для трех взаимно перпендикулярных площадок, полностью характеризуют напряженное состояние в точке, т. е. позволяют вычислить компоненты вектора напряжений на площадках, произвольно ориентированных относительно выбранной системы координат. Для этого рассмотрим элементарный объем, образованный сечением параллелепипеда, изображенного на рис. 4.2 плоскостью, пересекающей координатные оси и имеющей единичный вектор нормали

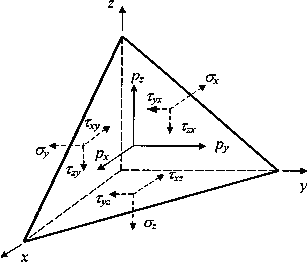
Рис.4.2. Элементарный четырехгранник с компонентами напряженного состояния.

п с компонентами n_x, n_y, n_z. На гранях полученного таким образом бесконечно малого тетраэдра действуют напряжения, показанные на рис. 4.2. При этом вектор напряжений p_n на наклонной площадке разложен па составляющие р_x, р_y, р_z вдоль координатных осей. Площади граней, ортогональных координатным осям и вектору нормали, обозначим соответственно dF_x, dF_y, dF_z, dF. Эти площади связаны между собой соотношениями

dFx=dFnx, dFy=dFny, dFz=dFnz

вытекающими из того, что грани, ортогональные координатным осям, есть проекции наклонной площадки на соответствующую координатную плоскость.

Проектируя силы, действующие на гранях элементарного тетраэдра, на координатные оси, получим уравнения равновесия для рассматриваемого объема. Например, проекции всех поверхностных сил на ось Ох дают

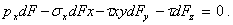
С учетом соотношений после сокращения на dF получим уравнение, связывающее проекцию р_x вектора напряжений с соответствующими компонентами тензора напряжений. Объединяя это уравнение с двумя аналогичными уравнениями, полученными проектированием сил на оси Оy и Оz, приходим к следующим соотношениям

носящим название формул Коши. Эти формулы определяют вектор напряжений на произвольно выбранной площадке с вектором п через компоненты тензора напряжений.

Формулы Коши позволяют вычислить через компоненты тензора напряжений

полное напряжение

нормальное напряжение

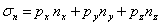
и касательное напряжение

Среди всех возможных направлений вектора нормали n существуют такие направления, для которых вектор напряжений p_n параллелен вектору п. На соответствующих площадках действуют только нормальные напряжения, а касательные напряжения отсутствуют. Такие площадки называются главными, а нормальные напряжения на этих площадках называются главными напряжениями. Пусть площадка с единичным вектором нормали является главной. Условия коллинеарности векторов p_n и n есть условия пропорциональности их компонент:

С учетом формул Коши получим систему линейных однородных уравнений относительно неизвестных компонент n_x, n_y, n_z вектора нормали к главной площадке

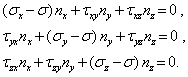
Эта система уравнений имеет ненулевое решение, если определитель, составленный из коэффициентов уравнений, обращается в нуль:

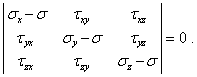
Раскрывая определитель, приходим к кубическому уравнению относительно главного напряжения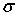

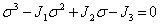
Здесь введены обозначения

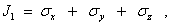
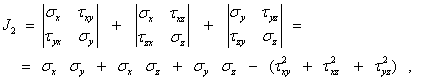
Выше написанное уравнение называется характеристическим уравнением для тензора напряжений. Коэффициенты этого уравнения называются инвариантами тензора напряжений. Решение кубического уравнения имеет три вещественных корня которые обычно упорядочиваются .

Каждому значению 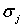(j =1, 2, 3) соответствует вектор n ^j, характеризующий положение j -й главной площадки, с компонентами n ^j₁, n ^j₂, n ^j₃. Для нахождения этих компонент достаточно в уравнения подставить найденное значение 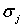и решить любые два из этих уравнений совместно с условием нормировки

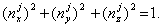
Главные напряжения обладают важным свойством: по сравнению со всеми другими площадками нормальные напряжения на главных площадках принимают экстремальные значения. Для доказательства этого свойства достаточно исследовать на экстремум нормальное напряжение как функцию n_x, n_y, n_z при дополнительном ограничении. Можно показать, что три главные площадки, соответствующие главным напряжениям , взаимно перпендикулярны или, что то же самое, векторы n^j и n^k, соответствующие различным значениям j и k —; ортогональны. Условие ортогональности имеет вид

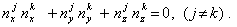
Кубическое уравнение можно переписать в виде

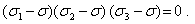
Получим следующие выражения для инвариантов через главные напряжения:

Термин «инвариантность» обозначает независимость объекта от выбора системы координат.

Введем среднее напряжение по формуле

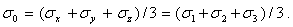
Тензор напряжений можно представить в виде суммы двух тензоров 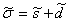, где

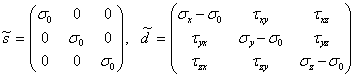
Первый тензор называется шаровым, он характеризует изменение объема тела без изменения его формы. Второй тензор, называемый девиатором, характеризует изменение формы. Особенностью девиатора напряжений является равенство нулю его первого инварианта:

Найдем положение площадок, на которых касательные напряжения принимают экстремальные значения. Для этого нужно отыскать экстремумы касательного напряжения. Экстремальные касательные напряжения действуют на площадках, параллельных одной из главных осей и образующих с двумя другими осями угол 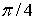. По величине эти напряжения равны

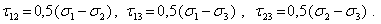
При этом на площадках с экстремальными касательными напряжениями присутствуют нормальные напряжения, которые равны

Глава 5. Плоское напряженное состояние

Рассмотрим важный для приложений случай плоского напряженного состояния, реализуемого, например, в плоскости Oyz. Тензор напряжений в этом случае имеет вид

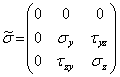
Геометрическая иллюстрация представлена на рис. 5.1. При этом площадки х= const являются главными с соответствующими нулевыми главными напряжениями. Инварианты тензора напряжений равны 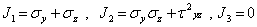, а характеристическое уравнение принимает вид

Корни этого уравнения равны

(5.1)

Рис. 5.1. Плоское напряженное состояние.

Рис. 5.2. Главные напряжения

Произвольная площадка характеризуется углом 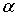на рис. 5.1 Нормальное и касательное напряжения на наклонной площадке выражаются через угол 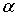следующим образом:

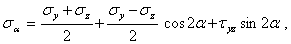
	(5.1)
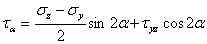
	(5.2)

Так как на главных площадках касательное напряжение отсутствует, то, приравнивая нулю выражение (5.2), получим уравнение для определения угла 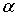между нормалью п и осью Оу

(5.3)

Наименьший положительный корень уравнения (5.1) обозначим через 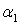. Так как tg(х)—периодическая функция с периодом 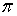, то имеем два взаимно ортогональных направления, составляющие углы 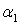и 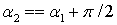с осью Оу. Эти направления соответствуют взаимно перпендикулярным главным площадкам (рис. 5.1).

Если продифференцировать соотношение (5.1) по 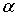и приравнять производную нулю, то придем к равенству (5.3).

Для нахождения ориентации площадок с экстремальными касательными напряжениями приравняем нулю производную от выражения

,

откуда получим

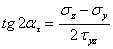
(5.4)

Сравнивая соотношения (5.3) и (5.4), находим, что

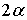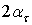Это равенство возможно, если углы и отличаются на угол . Следовательно, направления площадок с экстремальными касательными напряжениями отличаются от направлений главных площадок на угол 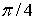(рис. 5.3).

Рис. 5.3. Экстремальность касательных напряжений

Величины экстремальных касательных напряжений получим после подстановки (5.4) в соотношение (5.2) и используя формулы

.

После некоторых преобразований получим

Сравнивая это выражение с полученными ранее значениями главных напряжений, выразим экстремальные касательные напряжения через главные напряжения

(5.5)

Дата добавления: 2015-06-30