Внецентренное растяжение и сжатие

Пример.

Для заданной схемы нагружения стержня (рис.52) построить эпюры поперечной силы Q_y(z) и изгибающего момента M_x(z) при следующих исходных данных: L = 5 кНм, P = 10 кН, q = 20 кН/м, l = 1 м.

Рис.52

Решение.

Запишем уравнения поперечных сил и изгибающего момента:

Q_y (z) = Q_y(0) │₁ – P - q×(z - l) │₂

M_x (z) = M_x (0) + Q_y(0)×z│₁ - P×(z - l) - q×(z - l)²/2│₂

В соответствии с условиями закрепления стержня запишем граничные условия в следующем виде: M_x (0) = - L,

M_x (3l) = 0.

Для нахождения неизвестной реакции Q_y (0) необходимо приравнять уравнение изгибающего момента к нулю при координате z = 3l:

M_x (3l) = M_x (0) + Q_y (0)×3l - P×(3l - l) - q×(3l - l)²/2 = 0.

Решая это уравнение относительно Q_y (0), получим Q_y (0) = 21.67кН.

Теперь, учитывая найденные константы, уравнения интегральных характеристик можно переписать в следующем виде:

Q_y (z) = 21.67│₁ – P – q×(z - l) │₂

M_x (z) = -L + 21.67z│₁ – P×(z - l) – q×(z - l)²/2│₂

Построение графиков будем производить аналогично примеру 1.

1 участок 0 ≤ z ≤ l:

Q_y (0) = 21.67 кН,

Q_y (l) = 21.67 кН,

M_x (0) = -5 кНм,

M_x (l) = -5 + 21.67*1 = 16.67 кНм.

2 участок l ≤ z ≤ 3l:

Q_y (l) = 21.67 – 10 = 11.67 кН,

Q_y (3l) = 21.67 – 10 – 20*(3 - 1) = -28.33 кН,

M_x (l) = -5 + 21.67*1 – 10(1 – 1) – 20(1 – 1) = 16.67 кНм,

M_x (3l) = -5 + 21.67*3 – 10(3 – 1) – 20(3 – 1) =0 кНм.

Определим координаты экстремума и значения функции изгибающего момента в экстремальной точке:

Q_y (z1) = 21.67 – P – q (z1 - l) = 0 → z1 = 1.58 м.

M_x (1.58) = -L + 21.67·1.58 – P (1.58 - l) – q (1.58 - l)²/2 = 20.07 кНм.

По рассчитанным значениям строятся графики поперечной силы и изгибающего момента (рис. 52).

При внецентренном растяжении равнодействующая внешних сил не совпадает с осью стержня, как при обычном растяжении, а смещена относительно оси z и остается ей параллельной (рис.53).

Рис.53

Пусть точка А приложения равнодействующей внешних сил имеет в сечении координаты (х₀, у₀). Тогда относительно главных осей равнодействующая сила Р дает моменты:

М_х = Р×у₀,

М_у = - Р×х₀.

Таким образом, внецентренное растяжение-сжатие оказывается родственным косому изгибу. В отличие от последнего, однако, при внецентренном растяжении в поперечном сечении стержня возникают не только изгибающие моменты, но и нормальная сила:

N=Р.

В произвольной точке В с координатами (х, у) нормальное напряжение определяется следующим выражением:

s = = .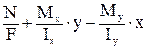

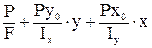Пространственная эпюра напряжений образует плоскость. Уравнение нейтральной линии получаем, приравнивая напряжения нулю:

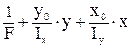=0. (100)

При внецентренном растяжении-сжатии в отличие от косого изгиба нейтральная линия не проходит через центр тяжести сечения. При положительных х₀ и у₀ по крайней мере одна из величин х или у, входящих в уравнение (100), должна быть отрицательной. Следовательно, если точка приложения силы Р находится в первом квадранте, то нейтральная линия проходит с противоположенной стороны центра тяжести через квадранты 2,3 и 4 (рис.54).

Рис.54

Расстояние от начала координат до некоторой прямой

ау+bх+с=0,

как известно из курса аналитической геометрии, равно

ОС = =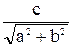

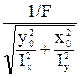
Следовательно, по мере того как точка приложения силы приближается к центру тяжести сечения, нейтральная линия удаляется от него.

В пределе при х₀=у₀=0, когда сила Р приложена в центре тяжести, нейтральная линия находится в бесконечности. Напряжения в этом случае распределены по сечению равномерно.

Из сказанного следует, что при внецентренном растяжении и сжатии нейтральная линия может как пересекать сечение, так и находится за его пределами. В первом случае в сечении возникают и растягивающие и сжимающие напряжения. Во втором случае напряжения во всех точках сечения будут одного знака.

В окрестностях центра тяжести существует область, называемая ядром сечения. Если след силы Р находится внутри ядра сечения, напряжения во всех точках сечения будут одного знака. Если сила приложена за пределами ядра сечения, нейтральная линия пересекает сечение, и напряжения в сечении будут как сжимающими, так и растягивающими. Когда точка приложения силы находится на границе ядра, нейтральная линия касается контура сечения. Чтобы определить ядро сечения, надо представить себе, что нейтральная линия обкатывается вокруг сечения. Точка приложения силы вычертит при этом контуры ядра.

ОГЛАВЛЕНИЕ

Основные понятия и определения…………………………………………………

Физическая и математическая модель…………………………………………….

Геометрические характеристики сечения…………………………………………

Изменение геометрических характеристик при параллельном переносе координатных осей………………………………………………………………….

Изменение геометрических характеристик при повороте координатных осей…

Геометрические характеристики сложных сечений………………………………

Метод сечений. Внутренние силы…………………………………………………

Напряжение. Напряженное состояние в точке тела………………………………

Интегральные характеристики напряжений в точке……………………………..

Нормальные напряжения в плоскости поперечного сечения……………………

Закон парности касательных напряжений………………………………………...

Напряжения на наклонных площадках……………………………………………

Главные площадки и главные напряжения……………………………………….

Экстремальные свойства главных напряжений. Круговая диаграмма Мора…..

Испытания материалов на растяжение. Диаграмма растяжения………………..

Математическая модель механики твердо деформируемого тела………………

Деформированное состояние тела…………………………………………………

Касательные напряжения при кручении………………………………………….

Касательные напряжения при изгибе. Формула Журавского……………………

Теории (гипотезы) прочности………………………………………………………

Растяжение (сжатие) стержней……………………………………………………..

Кручение стержней………………………………………………………………….

Изгиб стержней………………………………………………………………………

Внецентренное растяжение и сжатие………………………………………………

ЛИТЕРАТУРА

1. Феодосьев В.И. Сопротивление материалов: Учеб. для вузов. – М.: Наука., 1998. – 512 с.

2. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов. – М.: Высш.шк., 1995. – 560 с.

3. Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. – Киев.: Наукова думка, 1988. – 736 с.

4. Расчет прямых стержней на прочность. Метод.указания. С.А.Девятов, З.Н.Соколовский, Е.П.Степанова.2001.76с.

Дата добавления: 2015-06-30