Устойчивость сжатых стержней

На практике часто приходится решать задачу устойчивости сжатых стержней. Если стержень сжимать силами, действующими по оси, то он будет укорачиваться, сохраняя свою прямолинейную форму. При некоторых условиях прямолинейная форма равновесия может оказаться неустойчивой, а стержень начнет выпучиваться, искривляться. Это явление называется продольным изгибом, насту­пает оно тем скорее, чембольше длина стержня по сравнению с его поперечными размерами.

Конструкция должна удовлетворять не только условиям прочно­сти и жесткости, но и условиям устойчивости. Следовательно, кроме расчета на прочность и жесткоеть в ряде случаев необхо­дим расчет на устойчивость.

При расчете на устойчивость следует знать то наименьшее значение внешней нагрузки, при котором становятся возможными несколько различных форм равно­весия. Такая нагрузка называется критической.

Пока нагрузка меньше критической, возможна лишь одна устойчивая форма равно­весия. При решении задач на определение критических сил исполь­зуют различные критерии потери устойчивости.

Суть первого критерия устойчивости заключается в том, что наряду с начальным состоянием равновесия возникают новые со­седние равновесные формы. Такой подход к решению задач назы­вают статическим.

Ко второму критерию устойчивости относят энергетический метод. Суть этого критерия заключается в следующем: если энер­гия деформации окажется больше работы внешних сил, то очевидно, что система будет устойчива; если энергия деформации окажется меньше работы внешних сил, система будет неустойчива; при без­различном равновесии (в линейной постановке задачи) приращение энергии деформации должно быть равно работе внешних вид.

Третий критерий устойчивости состоит в исследовании движения системы, вызываемого некоторыми малыми возмущениями началь­ного равновесного состояния. Такой критерий называют динамичес­ким.

Критическая сила при потере устойчивости в упругой стадии вычисляется по формуле Эйлера

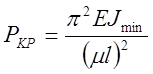
где J_min- минимальный момент инерции поперечного сечения стержня;

m - коэффициент приведения длины (см. табл. I).

Коэффициент приведения длины m зависит от характера

§ связей (линейные, угловые, абсолютно жесткие или упругие), наложенные на торцовые и промежуточные сечения стержня;

§ нагружения стержня внешними силами (сосредоточенные, распре­деленные);

§ изменения сечения с чэжня по его длине (постоянное, ступен­чатое, непрерывно переменное).

Допускаемая величина сжимающей силы

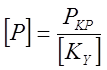
где [Ку]- допускаемый коэффициент запаса устойчивости, принимаемый:

для сталей -1,8..3,0 (меньшее значение для стоек с большей жесткостью)

для чугуна -[Ку] = 5..5,5

для дерева -[Ку] = 3...3.2..

Напряжения, возникавшие ч поперечном сечении стержня при Р = Ркр, называется критическими: -

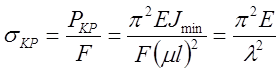
где 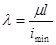- гибкость стержня,

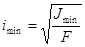
минимальный радиус инерции поперечного сечения стержня.

Дата добавления: 2015-06-30