Решение.Удлинение элементаdx

КРУЧЕНИИ И ИЗГИБЕ.

Деформации при растяжении-сжатии и кручении определяются по закону Гука:

; ;

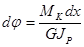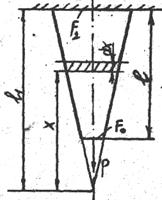Рис 18.

Полное перемещение (угол закручивания всего вала) равно алгебраической сумме перемещений (углов закручивания) отдельных участков (см. задачу 9):

;

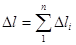Задача 10. Брус, имеющий форму усеченного конуса, растянут силой Р (рис.18). Определить его удлинение, счита, что длина бруса значительно больше его поперечных размеров.

Радиусы кругов усеченного конуса на уровне X обозначим через r_x, на уровне l₁ – через r₁. Тогда из подобия треугольников следует,

r_x/ r₁=x/l₁

отсюда

r_x= r₁· x/l₁

Площади соответствующих кругов равны pr²: F_x=pr_x², F₁=pr₁²

Следовательно

pr_x² = pr₁² x²/l₁²; F_x= F₁ x²/l₁²

Подставим значение F_x в формулу, выражающую закон Гука:

Удлинение бруса найдём, проинтегрировав последнее равенство:

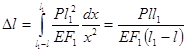
Учитывая что, ,окончательно получим:

Перемещение при изгибе (прогиб и угол поворота) могут быть определены либо с помощью универсального уравнения упругой линии балки, либо с помощью ЭВМ или интеграла Мора, либо способом Верещагина.

Остановимся более подробно на приёме Верещагина. Для того, чтобы использовать формулу Верещагина

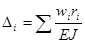
необходимо, чтобы площади грузовой эпюры изгибающих моментов были приведены к простейшим фигурам, для которых положение центров тяжести и величины площадей вычисляются элементарно. Это приводит к необходимости так называемого “ расслоения ” сложной эпюры на ряд самостоятельных эпюр. Рассмотрим это на примере.

Задача 11. Определить прогиб и угол поворота сечения В балки, загруженной так, как показано на рис. 19.

Если построить эпюру изгибающих моментов от всей внешней нагрузки (грузовую эпюру), то получим фигуры, площади и положения центров тяжести которых будут неизвестны. Поэтому всю нагрузку, действующую на балку, разбивают на ряд простых нагрузок (рис. 20).

Необходимо помнить, что криволинейные эпюры будут только на участках с распределённой нагрузкой. Поэтому для сосредоточенных сил и моментов можно построить грузовую эпюру без предварительной разбивки. Однако во избежание арифметических ошибок это делать не рекомендуется. Эпюры Мр для балок 1-4 приведены на рис. 21. Их построение ничем не отличается от приведённого выше. Однако при достаточном навыке эпюры можно построить исходя из дифференциальных зависимостей при изгибе.

В задаче требуется определить прогиб и угол поворота в сечении В, т.е. линейное и угловое перемещение правого конца балки. Для нахождения прогиба в искомом сечении прикладываем сосредоточенную силу 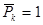и строим от этой нагрузки единичную эпюру (рис. 21, схема 5). Если определяем угол поворота, то в искомом сечении прикладываем сосредоточенный момент и вновь строим эпюру, но теперь уже от единичного момента (рис. 21, схема 6).

Как видим, грузовые эпюры остаются неизменными. Найдём их площади и обозначим положение их центров тяжести (рис. 21, схемы 1-4):

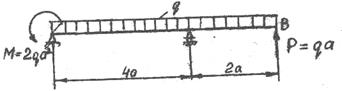
РИС. 19

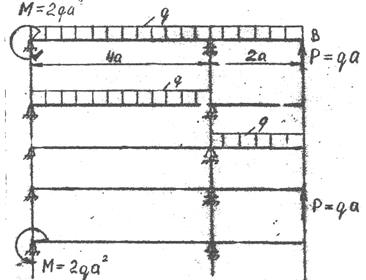
РИС. 20

РИС.21

; ; ;

; ;

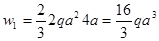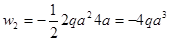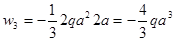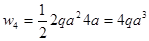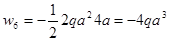
Ординаты единичных эпюр, расположенные под центрами тяжести грузовых эпюр, находят из подобия треугольников (рис. 21, схемы 5,6)

; ; ; ; ; ;

; ; ; .

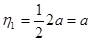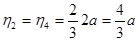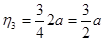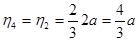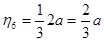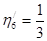Площади грузовой эпюры имеют те же знаки, что и сами эпюры. Знаки h_i зависят от направления единичных силовых факторов, которые принимаются произвольно. Если получили положительное перемещение, то это значит, что направление единичного силового фактора совпало с направлением перемещения.

Умножая w_i на h_i и учитывая, что EJ =const, для прогиба в сечении В получим (рис. 19).

=

= =

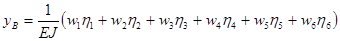Аналогично получим угол поворота сечения В:

=

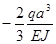
Как видим, угол поворота сечения В имеет направление, противоположное единичному моменту М_К.

Дата добавления: 2015-06-30