Статически неопределимые системы

Статически неопределимые системы – это такие системы, для которых определение реакций связей не может быть произведено при помощи уравнений равновесия.

Разность между числом неизвестных силовых факторов и числом независимых уравнений равновесия, которые могут быть составлены для рассматриваемой системы, есть степень статической неопределимости.

Для решения простейших статически неопределимых систем, стержни которых подвержены действию продольных сил, рекомендуется:

изобразить деформированное состояние системы. Связь между деформациями отдельных элементов этой системы записать в виде уравнения совместности деформаций (рис. 22, а; 23, а);

выделить часть системы, по отношению к которой искомые силовые факторы будут внешними силами, составить независимые уравнения равновесия (рис. 22, б; 23,б).

Направление продольных сил должно соответствовать принятому в изображённом деформированном состоянии направлению деформаций.

Так, в первом случае (рис. 22,б) усилие N₂ направлено на растяжение, так как перед D l ₂ стоит знак "плюс", т.е. в деформированном состоянии мы задались растяжением. Если бы перед D l ₂ стоял знак “минус”(D l ₁ - D l ₂ =d), то усилие N₂ необходимо было бы направить в обратную сторону (рис. 22, в).

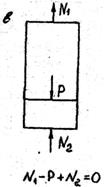
Рис. 22

Выразим деформации в уравнении совместности деформаций через закон Гука (рис. 22, а; 23, а):

;

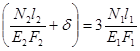
Где d – величина монтажного зазора, возникающего из-за неточности изготовления отдельных элементов конструкции.

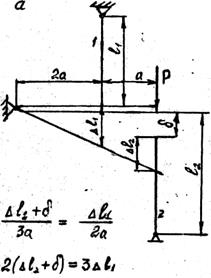
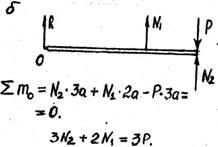
Рис. 23.

Дополнительные напряжения в статически неопределимых системах могут возникатьв случае изменения температуры её отдельных элементов. Температурная деформация оценивается по известной из курса физике формуле:

Dl₁=alDt;

где a - темперетурный коэффициент расширения [1/⁰С]

Знак температурной деформации определяется в зависимости от знака упругой деформации (рис. 23, а).

Пусть стержень 2 нагревается на величину Dt₂, тогда его общая деформация уменьшается на Dlt₂:

Если же нагревается стержень I, то

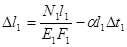
так как его общая деформация увеличивается.

Решить совместно полученную систему уравнений.

В машиностроении наиболее широко применяеся общий метод раскрытия статической неопределимости стержневых и рамных систем – метод сил.

Этот метод (метод сил) включает следующие основные этапы расчёта:

1. Устанавливается степень статической неопределимости.

2. Удаления дополнительных связей

3. Составляют э к в и в а л е н т н у ю систему.

4. Составляют канонические уравнения метода сил

5. Вычисление реакций и построение эпюр ВСФ обычным способом

1. Устанавливается степень статической неопределимости. Степень статической внешней неопределимости системы определяется числом избыточных опорных связей, т.е. разностью между числом неизвестных силовых факторов (реакций и реактивных моментов опор) и числом независимых уравнений равновесия статики (для плосокй системы сил –3).

Пример. Установить степень статической неопределимо­сти для рамы (рис. 24,а).

Рис. 24

Подвижная тарифная опора I: реакция R₁ такой опоры направлена по нормали к поверхности, на которую опираются катки подвиж­ной опоры, т. е. дает один силовой фактор.

Неподвижная шарнирная опора 2: реакция R₂ такой опоры про­ходит через ось шарнира и может быть разложена на две составляю­щие (дает два силовых фактора).

Жесткая заделка 3: дает три силовых фактора - составляющие R₃ и реактивный помет M_R3

В сопротивлении материалов неизвестные силовые факторы обоз­начают X_i. Следовательно, схема на рис. 24,а идентична схеме на рис. 24,6.

Таким образом, для заданной системы имеем шесть неизвестных силовых факторов, а число независимых уравнений равновесия равно 3, т. е. рама три раза статически неопределима: 6-3=3.

Кроме внешней статической неопределимости существует статическая неолределимость, вызванная дополнительными внутренними связями (внутренняя статическая неопределимость).

Всякий замкнутый контур является трижды статически неопределимой системой. Шарнир, включенный в узел, где сходятся n стержней, снижает степень статической неопределимости на единицу меньше числа сходящихся в нём стержней (n-1).

2. Путём удаления дополнительных связей заменяют исходную систему статически определимой, которая называется о с н о в н о й с и с т е м о й.

Основных систем может быть множество. Предпочтение отдают той, для которой определение перемещений будет наиболее простым.

3. Основную систему нагружают заданной нагрузкой, а в точках крепления удаленных связей прикладывают неизвестные силовые факторы X_i, заменяющие действие удалённых связей. Такая система носит название э к в и в а л е н т н о й.

4. Составляют канонические уравнения метода сил:

· · · · · · · · · · · · · · · · · · · · · ·

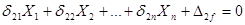
Число этих уравнений равно степени статической неопределимости системы. Напомним, что значения индексов перемещений означают:

Первый индекс отмечает точку и направление перемещения (адрес), второй – указывает причину, вызывающую данное перемещение.

Например, d₂₃ (рис. 24) обозначает вертикальное перемещение точки А, Вызванное действием силы Х₃=1.

5. После определения дополнительных неизвестных усилий производят вычисление реакций и построение эпюр ВСФ обычным способом.

З а д а ч а 12. Раскрыть статическую неопределимость для балки, изображённой на рис. 25.

Рис. 25

Решение. 1. Устанавливаем степень статической неопределимости 4-3=1 (подвижная опора даёт один силовой фактор, жесткая заделка – 3, всего 4, а число уравнений равновесия равно 3).

2. Изображаем основную систему. Таких систем может быть довольно много, наиболее простыми будут две (рис. 26):

Рис. 26.

Обе эти схемы, с точки зрения вычисления равноценны. Остановимся на второй схеме (рис. 26,б).

3. Изображаем эквивалентную систему (рис. 27,а). Легко за­метить, что неподвижная шарнирная опора отличается от жесткой заделки отсутствием реактивного момента.

Поэтому неизвестным силовым фактором, подлежащим определе­нию, и будет этот момент, обозначенный на схеме Х₁.

4. Составляем каноническое уравнение метода сил.

Так как задача один раз статически неопределима, то и уравнения будет одно:

X₁d₁₁ + D_1Р = 0

откуда

X₁ = -D_1Р/d₁₁

В нашем случае X₁ - реактивный момент, поэтому D_1Р и d₁₁ иесть углы поворота в точке приложения этого момента, от внешней нагрузки и единичного момента М_К=1 (соот­ветственно).

Перемещения могут быть определены любым способом (см. преды­дущую тему). Воспользуемся, например, приемом Верещагина. Для определения d₁₁ необходимо эпюру М_К (рис. 27,в) умножить саму на себя:

=

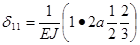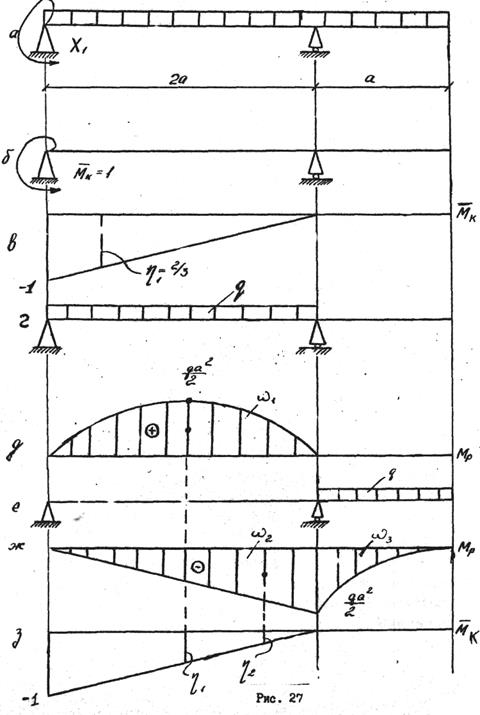
Заметим, что для любой стержневой системы d₁₁ >0.

Найдем значение D_1Р.

Для того разобьем внешнюю нагрузку на две так, как показано на рис. 27,г,е. Груговые эпюры от этих нагрузок представлены на рис. 27д,ж. На рис. 27,з вновь воспро­изведена единичная эпюра.

Последующие вычисления ясны из рисунка;

; ;

; ;

; ;

=-

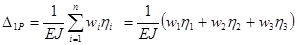
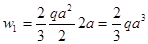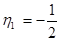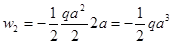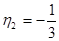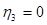Следовательно,

X₁ = -D_1Р/d₁₁ =

Дата добавления: 2015-06-30