Напряжения при растяжении-сжатии, кручении и изгибе

Угол a считается положительным в том случае, когда отсчёт ведётсяот наибольшего (алгебраически) главного напряжения до внешней нормали к искомой площадке против хода часовой стрелки.

Для решения прямой задачи исследования плоского напряженного состояния применяются следующие формулы:

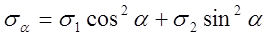
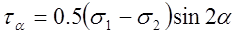
В обратной задаче заданы

напряжения по двум произвольным взаимно перпендикулярным площадкам (по закону парности касательных напряжений) a и b, s_a, s_b.

Необходимо найти величину и направление главных напряжений.

Решается эта задача по формулам:

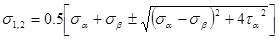
Напрявление главных напряжений определяется так же, как и в прямой задаче, но отсчёт угла a ведётся не от главного напряжения (ведь оно ещё неизестно), а от нормали к a –площадке, т.е. от s_a,.

Поэтому положительным будет направление по ходу часовой стрелки.

П р и м е ч а н и е. Приведённые формулы даны для главных напряжений s₁ и s₂. Если заданы другие главные напряжения, то в формулах меняются лишь индексы. Например:

Условие прочности при сложном напряжённом состоянии записывается в виде

s_ЭКВ =< [s]

где s_ЭКВ эквивалентное напряжение, вычисляемое по одной из теорий прочности:

s_{ЭКВ 1}=s₁

s_{ЭКВ 2}=s₁ m(s₂ +s₃)

s_{ЭКВ 3}=s₁ - s₃

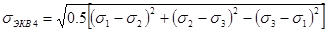
ПРИМ. В некоторых источниках коэфф. Пуассона - v ( e'=-ve ) обозначают m.

Деформации определяются по обобщённому закону Гука:

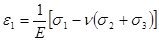
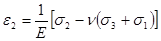
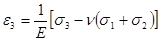
Если необходимо найти деформацию по какому-либо направлению в случае плоского напряжённого состояния, то необходимо воспользоваться формулой

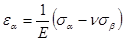
Величина s_b находится из равенства

s_a+s_b=s_max+s_min,

З а д а ч а 8. Определить аналитически и графически нормальные и касательные напряжения по указанному наклонному сечению в элементе, по граням которого известны нормальные и касательные напряжения (рис. 13, а).

Рис. 13

Р е ш е н и е. По граням элемента известны нормальные s_a и касательные t_a напряжения. Следовательно, s_a = 30 МПа; t_a=20МПа; s_b = - 30 МПа; t_b=-20 МПа.

Используя эти данные решим обратную задачу исследования напряжённого состояния и найдём величину и направление главных напряжений:

=

=0.5(30-30+-((30+30)²+4·20²)^0.5=+-36МПа.

По величине s^max_min проставляем индексы главных напряжений:

s₁ = 36 МПа; s₂ =0; s₃ = -36 Мпа.

Угол наклона главной площадки найдём по формуле

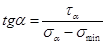=20/(30+36)=0.303

Откуда a= 17. Проведём вектор s₁ под углом в 17 по отношению к ветору s_a и перпендикулярно ему – главную площадку (рис. 13, б).

Графически эта часть задачи решается так: на плоскости s, t в масштабе отложим значения s_a и t_a (точка D_a, рис.14) затем значения s_b и t_b (точка D_b, рис.14). Отрезок D_a D_b пересечёт ось s в точке С. Это и будет центр круга Мора.

Отрезок СА = s₁, а СВ = s₃. направление s₁ получим, проведя луч из точки В через точку D_a^/.

В задаче требуется найти нормальные и касательные напряжения по площадке, зафиксированной наклонным сечением под углом 43⁰ по отношению к – площадке. Проведём нормаль к искомой площадке D_a^/ (рис. 13, в) и найдем угол a^/ между s₁ и нормалью n₀^/.

Как видно из рисунка, a^/=17 +43=60⁰,

Решим прямую задачу исследования плоского напряжённого состояния:

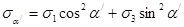=36cos²60 –36sin²60=-18МПа

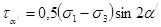=(36+36)/2 sin(2·60)=31.2МПа

Векторы 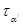и указаны на рис. 13, б.

Графически заключительная часть задачи решается достаточно просто: из точки В (рис. 14) проводят луч под углом a^/=60⁰ до пересечения с кругом в точке D_a^/. Координаты этой точки являются искомыми напряжениями.

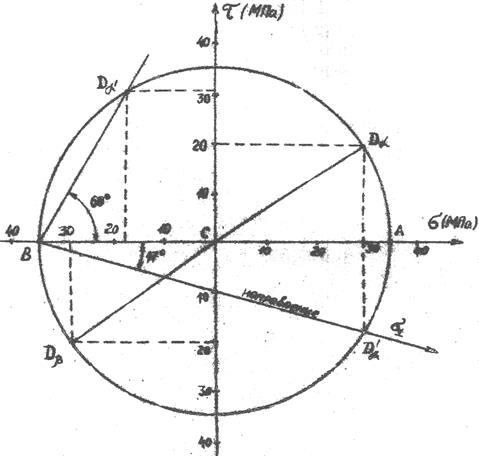
Рис. 14

РАБОТА №3 На тему "Напряженное состояние"

В задачах представлены три вида напряженного состояния: линейное, плоское и объемное. В зависимости от условия за­дачи необходимо определить различные искомые величины: глав­ные напряжения, напряжения на наклонных площадках, деформации под действием соответствущих напряжений и т.д.

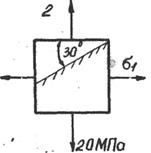
3-1	[s]=75MПа; Е=2·10^5MПа; m=0.25 1- Определить: А) sa; ta б)ea 2. Проверить прочность элемента по II теории прочности.	3-2	sэкв ^II =[s]=75MПа;Е=2·10^5MПа; m=0.25 Определить: s1 sa; ta ea.
Прим.	Прим.

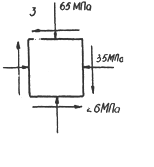
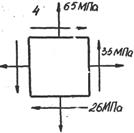
3-3	[s]=75MПа; Е=2·10^5MПа; m=0.25 Определить: а) главные напряжения. Б) Угол наклона, главных площадок в) e1, e2, e3. 2. Проверить прочность элемента по III теории прочности.	3-4	[s]=80MПа;Е=2·10^5MПа; m=0.3 2- 1. Определить: а) главные напряжения. Б) Угол наклона, главных площадок в) e1, ea 2. Проверить прочность элемента по II теории прочности.
Прим.	Прим.

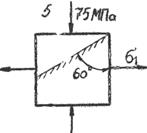
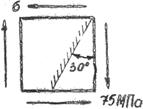
3-5	[s]=75MПа; Е=2·10^5MПа; m=0.25 Определить: а) главные напряжения. Б) Угол наклона, главных площадок в) e1, e2, e3. 2. Проверить прочность элемента по III теории прочности.	3-6	[s]=80MПа;Е=2·10^5MПа; m=0.3 1. Определить: а) главные напряжения. Б) Угол наклона, главных площадок в) e1, ea 2. Проверить прочность элемента по II теории прочности.
Прим.	Прим.

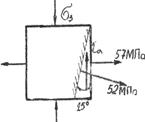
3-7	[s]=80MПа; Е=2·10^5MПа; m=0.3 Определить: а) s3, sb; ta. б) e1, e2, e3. 2. Проверить прочность элемента по II теории прочности.	3-8 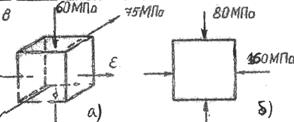Е=2·10^5MПа; m=0.3, e1=4,275·10^-4. Определить: какое из двух напряженных состояний опаснее с точки зрения 4 теории прочности.
Прим.	Прим.

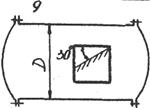
3-9	D=1m, d=0.01m, [s]=50MПа; q=1MПа; m=0.3 Определить: а) главные напряжения б)sa; ta 2. Проверить прочность элемента по II теории прочности.	3-10	D=1m, d=0.01m, [s]=90MПа;m=0.3 1. Определить: а) главные напряжения. б) ta в) q 2. Проверить прочность элемента по II теории прочности.
Прим.	Прим.

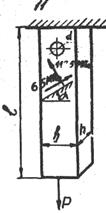
3-11	l=1m, b=0.12m, h=0.01m, d=0.02m, [s]=180MПа; q=1MПа; m=0.3, Е=2·10^5MПа Определить: а) a, s1, P, e, e^/ 2. Проверить прочность в ослабленном сечении.	3-12	д=1m, F=0.001m^2, [s]=160MПа;m=0.3, Е=2·10^5Mпа, P=15kH 1. Определить: a, s1, sa, e, e^/ 2. Проверить прочность элемента по I теории прочности.
Прим.	Прим.

3-13 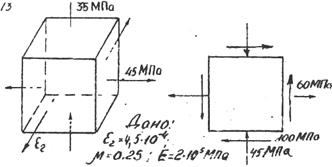Определить: какое из двух напряженных состояний опаснее с точки зрения 4 теории прочности.	3-14	[s]=40MПа;m=0.3,a=15^0 1. Определить: а) главные напряжения. б)sa; ta 2. Проверить прочность элемента по I I теории прочности.
Прим.	Прим.

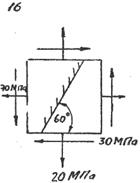
3-15	Определить: Угол наклона главной площадки. Г лавные напряжения. ta; tb	3-16	Определить: Г лавные напряжения. sa; ta
Прим.	Прим.

Нормальные напряжения при растяжении-сжатии распределены равномерно:

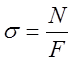
Условие прочности запишется так:

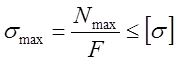
где [s] допускаемое напряжение

При решении задач необходимо обратить внимание на выбор опасного сечения.

Если F = const, то опасным сечением будет то, при котором N=N max. В ослабленных сечениях при определении напряжений учитывают площадь ослабленного сечения (площадь нетто Fн).

П р и м е р. Определим напряжение в опасном сечении стержня прямоугольного поперечного сечения (b x h), ослабленного отверстием диаметром d (рис. 15).

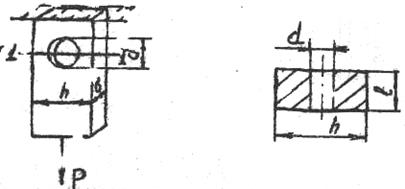Рис 15.

Опасным сечением является сечение I-I. Площадь ослабленного сечения:

F_н = bh –db = b (h – d).

Тогда

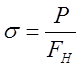= - P/(b(h-d))

При кручении воникают касательные напряжения t. Для стержней круглого сечения они распределены по закону треугольника (рис 16)

Рис 16.

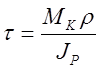
Максимального значения касательные напряжения достигают в точке контура сечения.

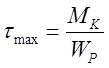
где W_P –полярный момент сопротивления сечения бруса (см. геометрические характеристики плоских сечений).

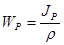
Дата добавления: 2015-06-30