Определим напряжение в точке А сечения 1-1

Для этого используем формулу для определения касательного напряжения в произвольнойточке сечения:

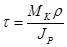
где М – крутящий момент;

r - расстояние от точки до центра вала;

J_P полярный момент инерции. 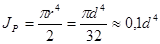для круга

Для точки А:

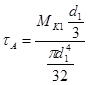=…=9.59 Мпа.

В сечении 2-2 необходимо определить напряжение в точке В, лежащей на контуре сечения. Известно, что точки, лежащие на контуре, имеют наибольшие напряжения, определяемые по формуле:

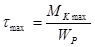
В нашем случае

где

Угол скручивания вала определяется по формуле:

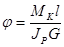
где М_K – крутящий момент на рассматриваемом участке;

l - длина рассматриваемого участка;

G- модуль упругости при сдвиге;

J_P полярный момент инерции.

Угол закручивания вала, состоящего из нескольких участков, равен алгебраической сумме углов закручивания каждого участка:

Для нашего случая:

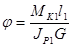+ =…=0.01728 рад.

При плоском изгибе двум видам внутренних усилий (М и Q) соответствуют два вида напряжений – нормальные s и касательные t_и:

; ;

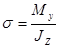Для решения задачи напомним известные формулы моментов инерции и моментов сопротивления сплошного круглого (диаметром d)

; ;

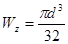и прямоугольного (b*h) сечений:

; ;

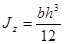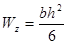Вычисление нормальных напряжений не вызывает затруднений. Остановимся более подробно на анализе формулы Журавского. Для любого сечения Q/J_z= const. Следовательно, t_и изменяются с изменением величины статического момента S_z(x). Статический момент вычисляется как произведение площади фигуры F_(y), расположенной на высоте y, на расстояние y_c от центра тяжести этой фигуры до центральной оси Z (рис.17):

S_z(x)= F_(y) y_c

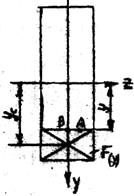Рис 17.

По ширине сечения касательные напряжения распределены равномерно: t_и^А=t_и^В (рис.17). Расчёт на прочность при изгибе несколько отличается от аналогичных расчётов при кручении и растяжении. Сначала из условия прочности по нормальным напряжениям

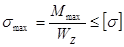находят величину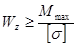

Зная момент сопротивления W_Z, определяют размеры сечения (для круглого и прямоугольного сечений по приведённым выше формулам, для прокатных профилей – из сортамента).

Затем принятое сечение проверяют на срез по условию:

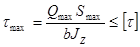
ОПРЕДЕЛЕНИЕ ПРЕМЕЩЕНИЙ ПРИ РАСТЯЖЕНИИ-СЖАТИИ,

Дата добавления: 2015-06-30