Москва 2009 3 страница

Суть этих способов заключается в том, что необходимо преобразовать комплексный чертеж так, чтобы рассматриваемый геометрический объект занял положение параллельное какой-либо плоскости проекций. Тогда на нее он, очевидно, спроецируется в натуральную величину.

Такое преобразование комплексного чертежа может быть осуществлено двумя основными способами:

1. Способом вращения, при котором оставляют неизменной систему плоскостей проекций, а меняют положение заданного геометрического объекта путем его вращения вокруг одной или последовательно вокруг двух подходящим образом выбранных осей так, чтобы интересующие нас прямые или плоскости оказались параллельными одной из плоскостей проекций. В качестве оси вращения обычно выбирают прямую, перпендикулярную одной из плоскостей проекций.

2. Способом замены плоскостей проекций, при котором оставляют неизменным положение в пространстве геометрического объекта, а заменяют одну или последовательно обе плоскости проекций так, чтобы интересующие нас прямые или плоскости оказались параллельными одной из новых плоскостей проекций.

Этими способами также можно решать задачи на приведение геометрических объектов в проецирующее положение.

4.1. Способ вращения вокруг проецирующей оси

Рассмотрим вращение точки А вокруг оси i, перпендикулярной горизонтальной плоскости проекций П ₁ (рис. 4.1). Ось вращения проецируется на плоскость П ₁ в точку, а на плоскость П ₂ - в прямую, перпендикулярную оси ОХ. Траекторией движения точки А будет окружность, лежащая в плоскости вращения, параллельной плоскости П ₁, с центром вращения в точке О, лежащей на оси, и с радиусом вращения ОА (рис. 4.1, а).

Траектория движения точки проецируется на плоскость П ₁ в натуральную величину, а на плоскость П ₂ - в виде прямой, параллельной оси ОХ. Радиус окружности проецируется на плоскость П ₁ в натуральную величину. Таким образом, горизонтальная проекция А ₁ точки А движется по окружности, а фронтальная проекция А ₂ - по прямой, параллельной оси ОХ.

Для того, чтобы повернуть точку А на угол j, откладывают этот угол на горизонтальной проекции (рис. 4.1, б) и получают горизонтальную проекцию А ₁ точки А в новом положении А ₁*. Фронтальную проекцию А ₂* этой точки находят с помощью линии проекционной связи, которую проводят из точки А ₁* до пересечения с прямой, проведенной из точки А ₂ параллельно оси ОХ.

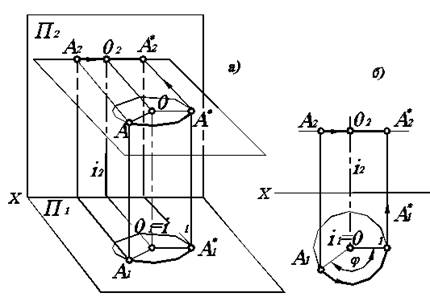
Рис. 4.1. Вращение точки вокруг горизонтально-проецирующей оси

4.2. Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения является частным случаем способа вращения вокруг проецирующей оси, с той лишь разницей, что геометрический объект можно не только вращать, но и перемещать вдоль плоскости, параллельной одной из плоскостей проекций.

При перемещении отрезка прямой в новое положение таким образом, что его крайние точки движутся параллельно какой-либо плоскости проекций, длина проекции отрезка на эту плоскость остается неизменной (рис. 4.2).

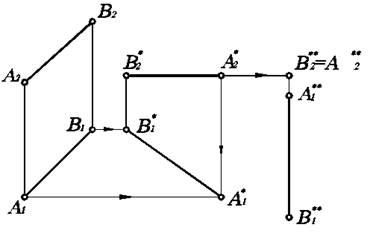
Рис. 4.2. Плоскопараллельное перемещение отрезка прямой.

Преобразуем последовательно отрезок прямой линии общего положения АВ в положение горизонтали, затем фронтально-проецирующее положение. Для этого расположим фронтальную проекцию А ₂ В ₂ отрезка АВ параллельно оси ОХ (А ₂* В ₂ * параллелен ОХ) в любом месте чертежа. При этом точки А ₁ и В ₁ перемещаются в новое положение по прямым, параллельным оси ОХ, и будут лежать на линиях связи с А ₂*, В ₂* соответственно. Тогда новая горизонтальная проекция займет положение А ₁* В ₁*. Очевидно, что А ₁* В ₁*- натуральная величина отрезка АВ, т.к. А * В * является горизонталью. Затем А ₁* В ₁* переместим в новое положение, чтобы А ₁** В ₁** была перпендикулярна оси ОХ. Тогда А ₂**= В ₂**, т.е. АВ займет положение проецирующей прямой. Следует заметить, что при определение натуральной величины АВ, которой является А ₁* В ₁*, удаленность проекции А ₂* В ₂* от оси ОХ не играет роли. Важно лишь выполнение двух требований: А ₂* В ₂* должна быть равна А ₂ В ₂ и параллельна оси ОХ.

4.3. Способ замены плоскостей проекций

Способ замены плоскостей проекций состоит в том, что одна из основных плоскостей проекций П ₁ или П ₂ заменяется новой плоскостью проекций П ₄, подходящим образом расположенной относительно изображаемого геометрического объекта, но перпендикулярной незаменяемой плоскости проекций.

В результате замены одной из основных плоскостей на плоскость проекций П ₄ получаем вместо старой системы плоскостей проекций П ₁/ П ₂ новую систему П ₁/ П ₄ (рис. 4.3), если заменялась плоскость П ₂, и систему П ₂/ П ₄, если заменялась плоскость П ₁.

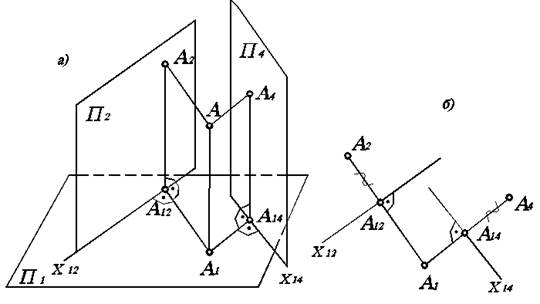
Рис. 4.3. Интерпретация способа замены плоскостей проекций

Например, на рис. 4.3, а плоскость П ₄ может выступать в роли фронтальной плоскости проекций П ₂. На рисунке 4.3, б, фигурными скобками отмечены расстояния от точки А до горизонтальной плоскости проекций П ₁. Естественно, как видно на рис. 4.3, а, эти расстояния равны А ₂ А ₁₂= А ₄ А ₁₄, так как высота точки А над плоскостью П ₁ проецируется как на П ₂, так и на П ₄ в виде одинаковых отрезков. Расстояние же до П ₂ и П ₄ от точки А могут быть различными, поэтому А ₁ А ₁₂¹ А ₁ А ₁₄.

Способ замены плоскостей проекций рационально применять при решении следующих задач:

- определение натуральной величины отрезка прямой линии;

- определение натуральной величины плоской фигуры;

- определение натуральной величины двугранного угла;

- определение кратчайшего расстояния от точки до прямой линии или до плоскости;

- определение кратчайшего расстояния между двумя параллельными или двумя скрещивающимися прямыми;

Решение задач данным способом рассмотрим на нескольких примерах.

4.3.1. Определение длины отрезка общего положения

Для определения натуральной величины (длины) отрезка АВ прямой линии необходимо сделать этот отрезок прямой линии общего положения в новой системе плоскостей проекций линией уровня. Чтобы отрезок АВ стал линией уровня относительно новой плоскости проекций, заменим плоскость П ₂ на плоскость П ₄, параллельную АВ, и перейдем от системы П ₁/ П ₂ к системе П ₁/ П ₄. Новую ось проекций X ₁₄, выбираем параллельно А ₁ В ₁ (рис. 4.4). Для построения новой проекции отрезка АВ проводим новые линии проекционной связи перпендикулярно оси Х ₁₄, и отмечаем на них новые проекции А ₄, В ₄ точек А и В. Для этого откладываем А _х1 А ₄= А ₂ А _х, В _х1 В ₄= В ₂ В _х.

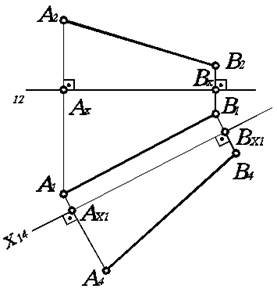
Рис. 4.4. Преобразование прямой общего положения в прямую уровня.

Соединяя найденные точки А ₄, В ₄, получаем новую проекцию А ₄ В ₄ отрезка АВ. Как видим, отрезок АВ в новой системе плоскостей проекций П ₁/ П ₄ является линией уровня, так как А ₁ В ₁ параллельна X ₁₄, а следовательно, АВ параллельна П ₄. Тогда, очевидно, что А ₄ В ₄ является натуральной величиной отрезка АВ.

4.3.2. Определение натуральной величины плоской фигуры

Для определения натуральной величины плоской фигуры необходимо дополнительную плоскость построить так, чтобы она была параллельна рассматриваемой фигуре, и тогда на эту плоскость проекций плоская фигура спроецируется в натуральную величину. Если в качестве плоской фигуры выбрать треугольник, тогда задача формулируется следующим образом: преобразовать плоскость треугольника общего положения в новой системе плоскостей проекций в плоскость уровня.

Одной заменой плоскостей проекций эту задачу решить невозможно, так как необходимо соблюдать условие: новая плоскость должна быть перпендикулярна незаменяемой. Поэтому решим эту задачу двумя заменами: первой заменой введем плоскость, которая перпендикулярна треугольнику АВС, второй заменой – плоскость, параллельную треугольнику АВС.

Для того, чтобы построить плоскость П₄, перпендикулярную треугольнику АВС, необходимо расположить ее так, чтобы она была перпендикулярна фронтали, либо горизонтали треугольника АВС.

Пусть П₄ перпендикулярна горизонтали, тогда новая ось Х ₁₄ должна быть перпендикулярна h ₁ (рис. 4.5).

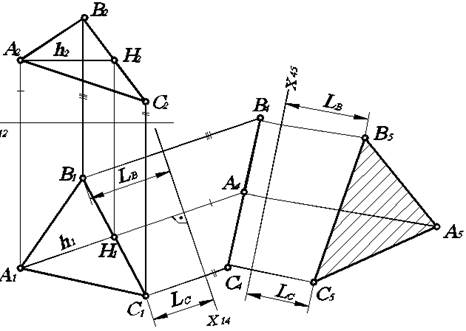
Рис. 4.5. Преобразование плоскости общего положения в плоскость уровня.

Построим ее на произвольном расстоянии от треугольника А ₁ В ₁ С ₁. Затем из точек А ₁, В ₁, С ₁ проведем линии связи перпендикулярно Х₁₄. На каждой из них от оси Х ₁₄ отложим отрезок, равный расстоянию от фронтальной проекции соответствующей точки до оси Х ₁₂. В результате получаем новую проекцию В ₄ А ₄ С ₄ треугольника АВС, которая представляет собой прямую, поскольку плоскость треугольника АВС перпендикулярна плоскости П₄.

Второй заменой вводим вместо П₁ плоскость П₅, параллельную плоскости треугольника АВС. Тогда получается система плоскостей проекций П₄/П₅, ось Х ₄₅ которой параллельна В ₄ А ₄ С ₄. Она может быть расположена на произвольном расстоянии от В ₄ А ₄ С ₄. Далее из точек В ₄ А ₄ С ₄ проводим линии связи перпендикулярно Х ₄₅, и на каждой из них от оси Х ₄₅ откладываем отрезок, равный расстоянию от горизонтальной проекции соответствующей точки до оси Х ₁₄. Получим точки А ₅, В ₅, С ₅, соединив которые имеем треугольник А ₅ В ₅ С ₅, который и является натуральной величиной треугольника АВС, поскольку в новой системе плоскостей проекций треугольник АВС параллелен плоскости П₅.

Вопросы для самоконтроля:

1. С какой целью осуществляется преобразование комплексного чертежа?

2. В чем заключается способ вращения вокруг проецирующей оси?

3. Назовите основные способы преобразования комплексного чертежа?

4. В чем сущность способа плоскопараллельного перемещения.

5. В чем заключается способ замены плоскостей проекций?

Тестовые задания

1. При каком положении плоской фигуры можно определить ее натуральную величину:

а) фигура перпендикулярна П₂;

б) фигура параллельна плоскости проекций;

в) фигура занимает общее положение.

2. Какие прямые используются в качестве осей вращения:

а) линии уровня;

б) проецирующие прямые;

в) прямые общего положения.

3. При каком положении плоской фигуры можно определить ее натуральную величину только одной заменой плоскости проекций:

а) если она занимает проецирующее положение;

б) если она параллельна одной из плоскостей проекций;

в) если она занимает общее положение по отношению к плоскостям проекций.

Глава 5. Многогранники

Многогранниками называются пространственные фигуры, состоящие из отдельных плоскостей (граней). Линии пересечения граней называются ребрами, которые представляют собой прямые линии.

5.1. Образование поверхностей многогранников

Образование любой поверхности можно представить как непрерывный ряд изображений, полученный при движении одной линии (образующей) по другой линии (направляющей). Поскольку и образующей и направляющей может быть произвольная кривая линия, то и поверхность может иметь любую произвольную форму, в общем случае достаточно сложную.

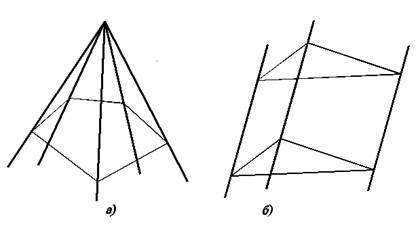
Рис. 5.1. Образование гранных поверхностей.

В том случае, когда образующая и направляющая являются прямыми линиями, получаем простейшую поверхность – плоскость. Если образующей является прямая линия, а направляющей ломаная, получаем гранную поверхность. Когда образующая закреплена в одной точке, при движении по направляющей она вычерчивает пирамидальную поверхность (рис. 5.1, а). Если образующая перемещается параллельно какому-либо направлению, получаем призматическую поверхность (рис. 5.1, б).

В дальнейшем из всех гранных поверхностей рассмотрим лишь призматическую и пирамидальную.

5.2. Точка и линия на поверхности многогранника

Ограничив призматическую поверхность двумя параллельными между собой плоскостями, пересекающими образующие, получаем призму. Ограничив пирамидальную поверхность одной плоскостью, будем иметь пирамиду. Тогда эти секущие плоскости называются основаниями многогранника, а образующие поверхности – боковыми поверхностями.

Рассмотрение образования боковых поверхностей многогранников с использованием таких понятий, как образующая и направляющая, играет большую роль в решении задач начертательной геометрии.

Построение любых проекций точек на поверхности многогранника осуществляется наиболее эффективно при помощи образующих и направляющих, хотя можно использовать и другие приемы.

Рассмотрим достаточно традиционную задачу построения проекций точек, лежащих на поверхности прямой пирамиды (рис. 5.2). Пусть заданы фронтальная и горизонтальная проекции пирамиды SABC и проекции точек 1₂, 2₂, 3₂. Надо построить третью проекцию пирамиды и отсутствующие горизонтальные и профильные проекции точек 1, 2, 3.

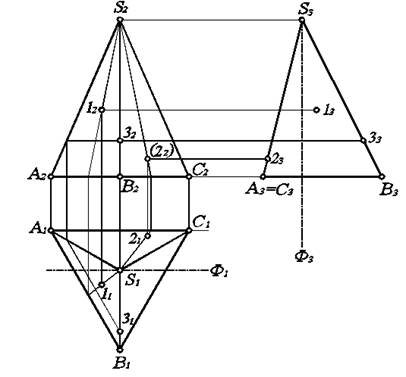
Рис. 5.2. Построение точек на поверхности пирамиды.

Для построения профильной проекции пирамиды через вершину S проведем фронтальную плоскость уровня. Тогда ее горизонтальная Ф₁ и профильная Ф₃ проекции будут служить базовыми линиями взамен традиционных осей проекций ОХ и ОY. Точку S ₃ получаем по линиям связи на базовой линии. Затем определяем положение точек А ₃= С ₃ и В ₃, откладывая от базовой линии Ф₃ отрезки, равные расстояниям от А ₁, С ₁, В ₁ до Ф₁ соответственно. Соединив точки основания вершиной, получаем профильную проекцию пирамиды. Как видим, грань SAC на профильной плоскости проекций вырождается в линию S ₃ A ₃ (или S ₃ C ₃).

Решим вторую часть задачи – построение отсутствующих проекций точек 1, 2, 3. Для определения положения горизонтальной проекции 1₁ используем образующую пирамиды: проведем через вершину S ₂ и точку 1₂ прямую до пересечения с ребром А ₂ В ₂ основания. Затем по линии связи получим горизонтальную проекцию этой точки на ребре А ₁ В ₁. Соединив полученную точку с вершиной S ₁, будем иметь горизонтальную проекцию образующей. На ней и лежит точка 1₁, положение которой определим по линии связи 1₂. Аналогично можно построить горизонтальную проекцию 2₁, с учетом того, что (2₂) – невидимая. Значит точка 2 лежит на грани SAC. Тогда основание образующей попадает на ребро АС основания. В остальном построения полностью повторяют предыдущие.

Однако для определения положения горизонтальной проекции 3₁ использовать образующую не представляется возможным, так как ребро SB, на котором лежит точка 3, в проекциях на П ₁, П ₂ дает вертикальную прямую (т.е. является профильной линией уровня). В этом случае используют линию, параллельную основанию. Через точку 3₂ проводят прямую, параллельную А ₂ В ₂, до пересечения с ребром S ₂ A ₂. Затем на ребре S ₁ A ₁ по линии связи получают горизонтальную проекцию точки пересечения, через которую проводят прямую параллельно А ₁ В ₁. Поскольку точка 3 лежит на этой прямой, то продолжая ее горизонтальную проекцию до пересечения с ребром S ₁ В ₁, получаем точку 3₁.

Профильную проекцию 1₃ строим на основании взаимосвязи между горизонтальной и профильной проекциями точки. А именно, откладываем по линии связи, проходящей через 1₂, от базовой линии Ф₃ вправо отрезок, равный расстоянию от 1₁ до Ф₁, как это делалось при построении профильной проекции пирамиды. Точка 2₃ лежит на пересечении горизонтальной линии связи, проходящей через 2₂, и грани S ₃ A ₃ C ₃, превратившейся в прямую S ₃ A ₃. Наконец, точку 3₃ находим на горизонтальной линии связи, проходящей через 3₂ и ребро S ₃ В ₃.

Следует заметить, что горизонтальную проекцию 3₁ можно найти через профильную. Для этого измеряем расстояния от 3₃ до Ф₃ и откладываем его вниз от Ф₁ по ребру S ₁ В ₁.

Линию на поверхности многогранника можно построить по характерным точкам, которыми являются точки ее изгиба и точки перехода через ребра. При этом следует помнить, что ломаная линия на поверхности многогранника будет ломаной, состоящей из отрезков прямой, в любой плоскости проекций, а кривая – кривой (за исключением частных случаев).

5.3. Позиционные задачи

В этом разделе рассматриваются позиционные задачи на определение общих элементов многогранника и более простых по сравнению с ним геометрических объектов, таких как прямая и плоскость, а также способы построения линии пересечения многогранников между собой.

5.3.1. Пересечение многогранника прямой

Для определения точек пересечения прямой и многогранника, так же как и в задаче о пересечении прямой и плоскости, необходимо через заданную прямую провести вспомогательную плоскость частного положения. Пусть требуется определить точки пересечения прямой а и призмы АВСА*В*С* (рис. 5.3).

Проведем через прямую а фронтально–проецирующую плоскость S. Тогда S₂= а ₂. Определим фронтальные проекции точек пересечения плоскости S с прямой а. Это точки 1, 2, 3, 4, где плоскость S пересекает ребра призмы. Их фронтальные проекции 1₂, 2₂, 3₂, 4₂ легко получить на линии а ₂. Ясно, что по этим точкам проходит фронтальная проекция 1₂2₂3₂4₂ плоской фигуры, полученной в результате пересечения S и призмы. Для построения ее горизонтальной проекции достаточно по линиям найти горизонтальные проекции 1₁, 2₁, 3₁, 4 точек, лежащих на соответствующих ребрах призмы, соединив которые получим искомую плоскую фигуру 1₁2₁3₁4₁. Стороны этого четырехугольника лежат на соответствующих гранях призмы.

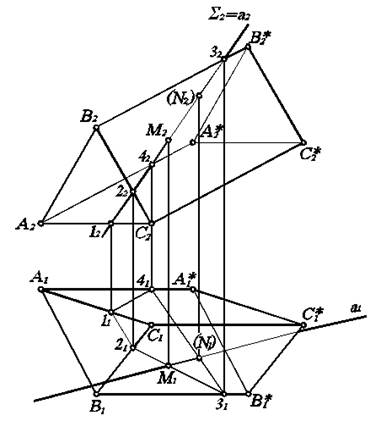
Рис. 5.3. Определение точек пересечения прямой и призмы.

Следовательно, зная видимость граней призмы, можно определить видимость сторон четырехугольника на П ₁: невидимой является лишь сторона 3₁4₁. Одно, что точки М ₁ и N ₁- горизонтальные проекции точек пересечения прямой а и призмы, так как они одновременно принадлежат и прямой а и линиям 23 и 34, лежащим на поверхности призмы. По линиям связи найдем положение точек М ₂ и N ₂, лежащих на а ₂.

Видимость определяется по принадлежности точек М и N граням призмы. Так как точка М ₁ лежит на видимой грани В ₁ С ₁ С ₁* В ₁*, то она видимая; точка N ₁ принадлежит невидимой грани А ₁ А ₁* В ₁* В ₁, следовательно она невидимая. Однако после «выхода»из призмы в точке N ₁ прямая а ₁ не сразу становится видимой, так как она остается закрытой гранями призмы. Аналогично определяем видимость точки М ₂, поскольку она принадлежит видимой грани В ₂ С ₂ С ₂* В ₂*, и невидимость точки N ₂, принадлежащей невидимой грани А ₂ А ₂* В ₂* В ₂. Невидимые участки прямой а обозначим пунктирной линией.

5.3.2. Натуральная величина сечения

Сечением многогранника называется плоская фигура, расположенная в секущей плоскости и ограниченная линиями пересечения ее с многогранником.

Часто приходится не только строить сечение многогранника плоскостью частного положения, но и определять натуральную величину сечения.. Рассмотрим эту задачу на примере сечения пирамиды горизонтально–проецирующей плоскостью S (рис 5.4). Пусть задана горизонтальная проекция S₁. Необходимо найти линию пересечения плоскости S с пирамидой и определить натуральную величину сечения. Таким образом, задача разбивается на две части: сначала надо построить сечение в плоскостях П ₁и П ₂, а затем определить его натуральную величину.

б)

а)

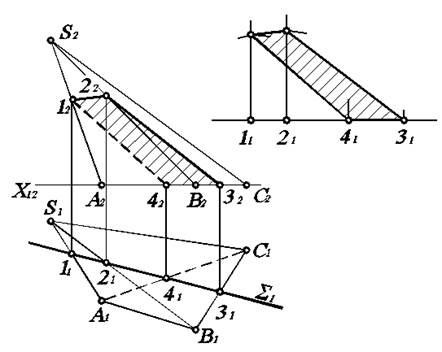
Рис. 5.4. Построение линии пересечения и определение натуральной величины сечения пирамиды плоскостью.

Чтобы решить первую часть задачи нужно найти все точки пересечения плоскости S с ребрами пирамиды и соединить их отрезками прямой. Горизонтальная проекция S₁ пересекает ребра пирамиды в точках 1₁, 2₁, 3₁, 4₁ (рис. 5.4, а). По линиям связи находим их фронтальные проекции 1₂, 2₂, 3₂, 4₂ на фронтальных проекциях соответствующих ребер. Соединяя найденные точки, получаем линию пересечения 1₂2₂3₂4₂ заданной плоскости с пирамидой. Отрезок 1₂4₂ этой линии будет невидимым, так как он лежит на невидимой грани A ₂ S ₂ C ₂. Плоская фигура, ограниченная полученной линией (на рис. 5.9, а заштрихована), и является сечением пирамиды плоскостью. В нашем примере это четырехугольник 1234.

Для определения натуральной величины четырехугольника 1234 способом замены плоскостей проекций не обязательно строить новую ось параллельно S₁ (или 1₁2₁4₁3₁), ввиду ограниченности площади чертежа. Достаточно соблюдать основные принципы построения. Начертим новую ось на свободном поле чертежа. Перенесем на нее точки 1₁,2₁,4₁,3₁, не меняя расстояния между ними. Проведем через них перпендикуляры к оси. Затем отложим на построенных перпендикулярах отрезки, равные расстояниям от оси П ₂/ П ₁, которую считаем расположенной на основании А ₂ В ₂ С ₂ пирамиды, до соответствующих проекций 1₂, 2₂, 4₂, 3₂. Соединив указанные точки, получим натуральную величину сечения пирамиды заданной плоскостью S (рис. 5.4, б).

Как видим, сечение в натуральную величину отличается от 1₂2₂3₂4₂ лишь тем, что оно вытянуто вдоль S₁.

5.3.3. Пересечение двух многогранников

При пересечении двух многогранников общим геометрическим элементом является замкнутая ломаная линия, состоящая из участков прямой, так как многогранники образованы из плоскостей, а линия пересечения плоскостей представляет собой прямую. Точки излома получаются в местах пересечения граней одного многогранника с ребрами другого.

В том случае, когда один из многогранников занимает частное положение (т.е. его боковые грани проецируются на одну из плоскостей проекций в многоугольник), задача построения линии их пересечения решается достаточно просто. Ввиду того, что одна из проекций многогранника – многоугольник, проекция линии пересечения на эту плоскость проекций совпадает с ним. Поскольку линия пересечения многогранников принадлежит каждому из них, то задача сводится к построению отсутствующих проекций ломаной линии, а следовательно, к построению проекций точек на поверхности многогранника и соединению из отрезками прямой. Заметим, что частное положение может занимать лишь призма, так как только ее можно расположить таким образом, чтобы боковые ребра, а значит, и грани были перпендикулярны плоскости проекций.

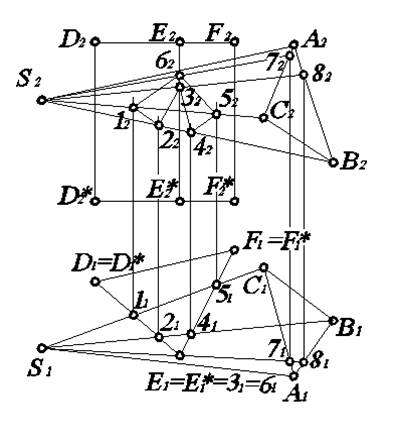
Рассмотрим описанные приемы построения на примере. Пусть пересекаются пирамида и призма частного положения (рис. 5.5). Требуется построить проекции линии их пересечения.

Поскольку призма расположена так, что все ее боковые грани перпендикулярны П ₁, то на П ₁ ее боковая поверхность проецируется в линию, точнее в треугольник D ₁ E ₁ F ₁. И горизонтальной проекцией линии пересечения призмы DEFD*E*F* и пирамиды SABC является ломаная линия 1₁ Е ₁5₁. Таким образом, горизонтальная проекция линии пересечения призмы и пирамиды получена без каких бы то ни было дополнительных построений. Следует учитывать, что грани призмы пересекают не только грань SAC, но и грани SBC и SAB пирамиды, что очевидно из рассмотрения чертежа на П ₁. Следовательно, можно отметить все точки излома линии пересечения 1₁ Е ₁5₁, расположенные на пересечении ее с ребрами пирамиды. А именно, точки 1₁, 2₁, 3₁, 4₁, 5₁, 6₁. Очевидно, что 3₁=6₁, так как ребро ЕЕ* призмы пересекает две грани SAB и SAС пирамиды.

Линия пересечения на каждой из проекций должна быть замкнутой. Причем ясно, что можно соединять отрезками прямой лишь точки, лежащие на одной и той же грани. Эти правила универсальны, и относятся к любой задаче о пересечении многогранников.

Дата добавления: 2015-06-30