Москва 2009 4 страница

Рис. 5.5. Построение линии пересечения пирамиды и призмы частного положения.

Тогда на П ₁ получаем горизонтальную проекцию линии пересечения призмы и пирамиды в виде ломаной 1₁2₁3₁4₁5₁6₁1₁, лежащей на гранях пирамиды (вместе с тем и призмы).

Для нахождения фронтальной проекции этой линии необходимо решить задачу построения проекций ломаной линии на поверхность пирамиды. Достаточно построить фронтальные проекции указанных точек. Так как точки 1, 2, 4, 5 лежат на ребрах пирамиды, то их фронтальные проекции 1₂, 2₂, 4₂, 5₂ легко получить по линиям связи. Для нахождения фронтальных проекций 3₂ и 6₂ точек 3 и 6, лежащих на гранях SAB и SAС соответственно, необходимо через точки 3₁ и 6₁ провести образующие S ₁7₁ и S ₁8₁. Точки 7 и 8 лежат на основании пирамиды, поэтому по линиям связи можно найти фронтальные проекции 7₂ и 8₂ на соответствующих ребрах основания А ₂ С ₂ и А ₂ В ₂ пирамиды. Построив фронтальные проекции S ₂7₂ и S ₂8₂ образующих, по линиям связи отметим на них точки 3₂ и 6₂. Соединив точки, получим замкнутую ломаную 1₂2₂3₂4₂5₂6₂1₂. Последовательность соединения определяется по горизонтальной проекции на основании правила принадлежности соседних точек пересечения одной и той же грани. Например, ошибочным было бы соединение точек 1₂ и 3₂, так как одна из них лежит на ребре S ₂С₂, а другая на грани S ₂ A ₂ B ₂.

Видимость точек и линий на П ₂ определяется по принадлежности граням пирамиды, так как обе грани D ₂ E ₂ E ₂ *D ₂ * и Е ₂ F ₂ F ₂ *E ₂* являются видимыми. Поскольку грани S ₂ A ₂ С ₂ и S ₂ В ₂ С ₂ невидимые, то и точки, и прямые, лежащие на них, также невидимые. Проведя невидимые линии пунктиром, получим решение в окончательном виде.

5.4. Развертка многогранника

Разверткой многогранника называется плоская фигура составленная из его граней, развернутых на одну плоскость.

5.4.1. Развертка призмы. Методы нормального сечения и раскатки.

Для развертки призмы применяют два метода: нормального сечения и раскатки. Рассмотрим последовательно каждый из них.

А. Метод нормального сечения.

Пусть требуется построить развертку наклонной трехгранной призмы АВCDEF (рис. 5.6).

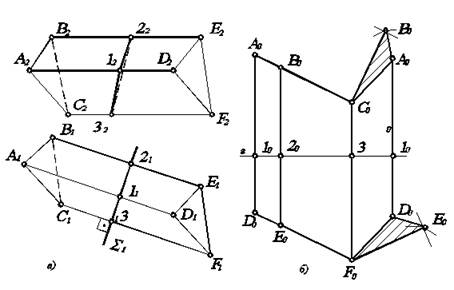
Рис. 5.6. Развертка наклонной трехгранной призмы.

Пересечем призму АВCDEF плоскостью S₁, перпендикулярной к боковым ребрам призмы. Построим сечение заданной призмы этой плоскостью – треугольник 123. Определим длины сторон треугольника 123. В свободном поле чертежа проведем прямую линию а (на рис. 5.6 прямая линия проведена горизонтально). От произвольной точки 1₀, взятой на этой прямой, отложим отрезки 1₀2₀, 2₀3₀, 3₀1₀, равные сторонам треугольника 123. Через точки 1₀, 2₀, 3₀, 1₀ проведем прямые, перпендикулярные прямой а, и отложим от точек 1₀, 2₀, 3₀, 1₀ отрезки, равные соответствующим длинам боковых ребер (1А, 1D, 2В, 2Е,…). Полученные точки А ₀, В ₀, C ₀, A ₀ и D ₀, E ₀, F ₀, D ₀ соединяем прямыми. Плоская фигура А ₀ В ₀ C ₀ A ₀ D ₀ F ₀ E ₀ D ₀ представляет собой развертку боковой поверхности призмы.

Чтобы получить полную развертку призмы, необходимо к развертке боковой поверхности пристроить основание призмы – треугольники АВС и DЕК, предварительно определив их неискаженные размеры.

5.4.2. Развертка пирамиды методом треугольников (триангуляции)

Для развертки боковой поверхности пирамиды применяют метод треугольников (триангуляции), который заключается в построении последовательно каждой боковой грани пирамиды, представляющей собой треугольник.

Пусть требуется сделать развертку четырехгранной пирамиды SABCD (рис. 5.7, а).

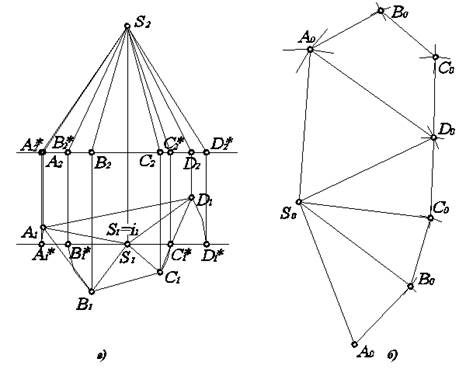
Рис. 5.7. Развертка пирамиды.

Сначала определим натуральную величину каждого из боковых ребер. Удобнее использовать способ вращения вокруг проецирующей оси. За ось i выбираем горизонтально–проецирующую прямую, проходящую через вершину S пирамиды. Вращаем проекции точек А ₁, В ₁, С ₁, D ₁ вокруг S ₁ до совмещения с горизонтальной прямой, проходящей через S ₁. Тогда горизонтальные проекции боковых ребер пирамиды примут новое положение S ₁ A ₁*, S ₁ B ₁*, S ₁ C ₁*, S ₁ D ₁*, параллельно горизонтальной оси проекций, т.е. ребра SA, SB, SC, SD будут приведены в положение фронталей. Как известно, фронталь проецируется без искажений (т.е. в натуральную величину) на П₂. Остается получить фронтальные проекции боковых ребер в новом положении, после вращения. В соответствии со способом вращения вокруг проецирующей оси, в то время, когда одна из проекций точки вращается вокруг оси, другая перемещается по горизонтальной линии. На горизонтальных линиях, проходящих через точки А ₂, В ₂, С ₂, D ₂, находим их новое положение А ₂*, В ₂*, С ₂*, D ₂* по линиям связи с А ₁*, В ₁*, С ₁*, D ₁* соответственно. Тогда отрезки S ₂ A ₂*, S ₂ B ₂*, S ₂ C ₂*, S ₂ D ₂* и являются натуральными величинами каждого из боковых ребер.

Таким образом, предварительные построения закончены, теперь вычертим развертку боковой поверхности пирамиды. Для этого необходимо знать натуральную величину ребер основания пирамиды. В данном случае не требуется никаких дополнительных построений, так как основание пирамиды – четырехугольник АВСD – занимает положение горизонтальной плоскости уровня, о чем свидетельствует то, что его фронтальная проекция А ₂ В ₂ С ₂ D ₂, представляет собой прямую, параллельную горизонтальной оси проекций. Следовательно, длина проекций A ₁ B ₁, B ₁ C ₁, C ₁ D ₁, D ₁ A ₁ является натуральной величиной соответствующих ребер.

Построение развертки боковой поверхности начинаем с вычерчивания первой грани, например, SAB, в натуральную величину. Для этого на свободном поле чертежа поставим точку S ₀ (рис. 5.7, б). Через нее проведем прямую линию в произвольном направлении. На ней отложим длину SA=S ₂ A ₂ *, получим точку А ₀. Чтобы построить первую грань SAB, осталось определить положение точки В. Для этого из точки А₀ проведем дугу окружности радиусом АВ=А₁В ₁, а из точки S ₀ радиусом SB=S ₂ B ₂ * На их пересечении и лежит точка В ₀. Соединив точки S ₀, A ₀, B ₀, получим грань SAB. Далее, проводя из точки В ₀ дугу радиусом ВС=В ₁ С ₁, а из точки S ₀ дугу радиусом S ₂ C ₂ *, на их пересечении получим точку С ₀. Аналогично строятся остальные боковые грани пирамиды.

Чтобы развертка была полной, необходимо дочертить к одному из ребер основания пирамиды четырехугольник A ₁ B ₁ C ₁ D ₁, аналогично тому, как это сделано в предыдущей задаче.

В случае, когда основание пирамиды занимает общее положение в пространстве, необходимо либо определить его натуральную величину способом замены плоскостей проекций, либо способом вращения вокруг проецирующей оси найти натуральную величину каждого ребра основания.

Вопросы для самоконтроля:

1. Как образуется поверхность призмы?

2. В какой последовательности решается задача на определение точек пересечения прямой и многогранника?

3. Как образуется поверхность пирамиды?

4. Какие вы знаете способы построения натуральной величины сечения?

5. Каким способом строят развертки поверхностей пирамиды?

Тестовые задания

1. Что называется разверткой поверхности?:

а) плоская фигура, которая получается путем совмещения всех точек поверхности с плоскостью;

б) плоская фигура, которая получается путем совмещения части точек с другой поверхностью;

в) П₁.

2. Что представляет из себя линия пересечения двух гранных поверхностей

а) плоскую ломаную;

б) пространственную ломаную;

в) плоскую кривую.

3. Задача на построение прямой на поверхности многогранника сводится:

а) к построению прямой на плоскости;

б) к построению кривой на плоскости;

в) к построению ломаной на плоскости.

Глава 6. Кривые поверхности

В начертательной геометрии поверхность рассматривается как множество последовательных положений некоторой линии – образующей поверхности, перемещающейся в пространстве определенным образом по другой линии, которую называют направляющей.

Образующая поверхности в процессе движения может изменять свою форму. Одна и та же поверхность может быть образована перемещением различных линий.

Поверхности можно разбить на классы:

1) линейчатые поверхности;

2) винтовые поверхности;

3) циклические поверхности;

4) поверхности вращения.

Наибольшее распространение в технике получили поверхности вращения.

6.1. Поверхности вращения

Поверхности вращения образуются при вращении некоторой произвольной линии вокруг оси. В этом случае образующей является указанная линия, а направляющей - окружность. Форма поверхности вращения определяется формой образующей.

Пусть произвольная линия AGEB вращается вокруг оси i. Тогда она образует поверхность вращения (рис. 6.1).

Линия пересечения поверхности вращения плоскостью, проходящей через ось i, называется меридианом (например A*G*E*B*). Меридиан, лежащий в плоскости, параллельной П ₂, называется главным. Линия пересечения поверхности вращения плоскостью, перпендикулярной оси i, называется параллелью. Таковыми являются направляющие, проходящие через точки АА *, ВВ *, ЕЕ *, GG *. Параллель, проходящая через наиболее удаленную от оси точку Е образующей, называется экватором, а через самую близкую точку G – горлом. Очевидно, что все параллели представляют собой окружности.

Одной из самых простых поверхностей вращения является цилиндр. Цилиндрическая поверхность образуется при вращении прямой (образующей) АВ вокруг оси (рис. 6.2, а). Образование цилиндрической поверхности подобно получению призматической с той лишь разницей, что у гранной поверхности направляющей является ломаная линия.

Рис. 6.1. Образование поверхности вращения.

В случае образования конической поверхности прямая AS, вращающаяся вокруг оси, закреплена в некоторой точке S на оси (рис. 6.2, б). Такая поверхность подобна пирамидальной, у которой образующей является тоже прямая, но перемещающаяся по ломаной линии. Для того, чтобы получить цилиндр или конус, надо соответствующую поверхность ограничить плоскостями основания.

Рис. 6.2. Образование поверхности цилиндра, конуса, сферы.

Если в качестве образующей выбираем окружность, то при ее вращении вокруг оси получаем:

- сферу, когда ось вращения проходит через центр О окружности (рис. 6.2, в);

- тор, в противном случае (рис. 6.3).

Если ось вращения проходит через образующую–окружность, тор получается закрытым (рис. 6.3, а), в противном случае-открытым (рис. 6.3, б). Примером открытого тора может служить бублик, закрытого – яблоко.

Рис. 6.3. Образование поверхности тора.

6.2. Точка и линия на поверхностях вращения

Рассмотрим в качестве примера построение точки и линии на некоторых поверхностях вращения.

6.2.1. Конус

А. Построить отсутствующие проекции точек А и В, расположенных на поверхности прямого кругового конуса, если известно положение А ₂ и В ₂ (рис.6.4).

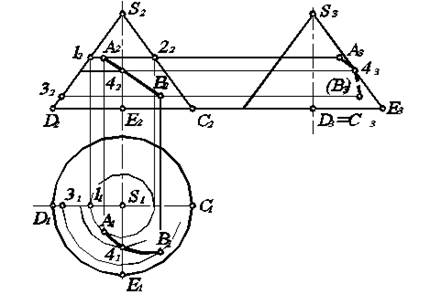
Рис. 6.4. Построение проекций точек и линии на поверхности конуса.

Для построение горизонтальной проекции точки, например А, необходимо через ее фронтальную проекцию провести горизонтальную линию. Тогда на П ₁ эта линия 12 представляет собой дугу окружности диаметром 1₂2₂=1₁2₁. По линии связи на ней находим А ₁. Аналогично, проводя дугу окружности радиусом S ₁3₁, равным расстоянию от оси конуса до точки 3₂ на его контуре, определяем положение на ней точки В ₁. По этим проекциям находим положение А ₃, В ₃.

В. По известной проекции А ₂ В ₂ линии на поверхности конуса построить горизонтальную и профильную.

Выбрав на линии А ₂ В ₂ промежуточную точку 4₂, найдем 4₁ так же, как сделали это для точек А и В. Соединив точки А ₁, 4₁, В ₁, получим горизонтальную проекцию линии АВ.

Для построения профильной проекции А ₃ В ₃ необходимо найти положение контурной точки 4, лежащей на SA. По фронтальной проекции 4₂, лежащей на S ₂ A ₂, находим профильную проекцию 4₃, лежащую на S ₃ A ₃. Теперь точки А ₃, 4₃, В ₃ можно соединить линией.

При соединении точек линией всегда надо руководствоваться достаточно очевидным правилом: на каждой проекции точки, принадлежащие линии, следует соединять в одинаковой последовательности. Так, если на фронтальной проекции точка 4 является промежуточной, то она будет промежуточной и на других проекциях.

6.2.2. Сфера

Проекцией сферы на любую плоскость проекций является окружность.

А. Рассмотрим построение проекций точек на поверхности сферы (рис. 6.5). Задача состоит в том, чтобы по известным проекциям построить отсутствующие. Для упрощения решения необходимо все характерные точки сферы обозначить. Точки, лежащие на экваторе, обозначим через А, В, С, D; точки, лежащие на главном меридиане – А, Е, С, F. Очевидно, что точки А и С принадлежат одновременно и экватору, и главному меридиану.

При построении проекций следует иметь ввиду, что любая параллель на П ₂ проецируется в горизонтальную прямую, а на П ₁ в окружность.

Пусть задана фронтальная проекция точки М. Проведем через нее параллель. Тогда на П ₂ получим горизонтальную прямую, проходящую через точку М ₂. А на П ₁ – дугу окрудности радиусом F ₁1₁, равным расстоянию от вертикальной оси до токи 1₂. Ясно, что точка М ₁ лежит на этой окружности. По двум проекциям М ₁ и М ₂, используя правило взаимосвязи проекций, построим М ₃.

Рассмотрим другую точку N, проекция которой N ₂ на П ₂ является невидимой. Аналогично предыдущему построим N ₁, лежащую на дуге окружности радиусом F ₁2₁. Так как N ₂ - невидимая, то N ₁ лежит выше оси Ф₁. А поскольку точка N находится на поверхности нижнего полушария, что видно из положения N ₂, то N ₁ - невидимая. Профильная проекция N ₃ строится по известному правилу взаимосвязи проекций. При этом, так как N ₁ лежит выше оси Ф₁, то N ₃ - левее Ф₃. Поскольку точка N лежит в правом полушарии, то на П ₃ она невидимая, так как на П ₃ все правое полушарие закрыто от нас левым и является невидимым.

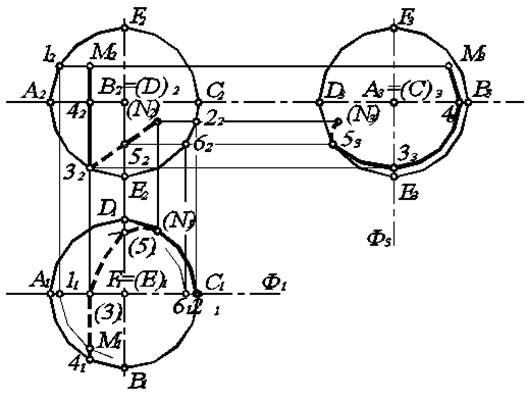
Рис. 6.5. Построение проекций точек и линии на поверхности сферы.

Видимость и невидимость полушарий, а следовательно, и точек, лежащих на них, можно легко определить, рассматривая с разных точек зрения обыкновенный резиновый мячик, нарисовав на нем экватор и два меридиана, расположенных в плоскостях, перпендикулярных друг другу.

В. Построим горизонтальную и профильную проекции линии МN, если известна ее фронтальная проекция М ₂ N ₂, состоящую из прямолинейных отрезков М ₂3₂ и 3₂ N ₂.

Очевидно, что точка 3₁ лежит на А ₁ Е ₁, так как 3₂ - на А ₂ Е ₂. При этом прямая МN проходит через экватор (точка 4₂). Следовательно, на П ₁ – через точку 4₁. А участок 4₁3₁ – невидимый, поскольку, как видно по его фронтальной проекции 4₂3₂, он лежит в нижнем полушарии, т.е. ниже экватора.

Для построения проекций участка 3 N выберем промежуточную точку 5₂. Тогда точка 5₁ лежит на дуге окружности радиуса 5₂6₂. Соединив точки 3₁, 5₁, N ₁, получим искомую линию М ₁4₁3₁5₁ N ₁.

Построим профильную проекцию М ₃ N ₃, которая проходит через те же промежуточные точки. Так как М ₂3₂ – вертикальная прямая, то на П ₃ она представляет собой дугу М ₃3₃ окружности радиуса 4₂3₂=А₃3₃. Точка 5₃ – контурная для профильной проекции сферы. Значит, остается соединить точки 3₃, 5₃, N₃ кривой линией. При этом участок 5₃ N ₃ – невидимый.

Если в нашу задачу входит более точное построение проекций линии MN, тогда на всех участках, где ее проекции не являются отрезками прямой или окружности, необходимо выбрать несколько промежуточных точек.

6.3. Пересечение поверхности вращения и многогранника.

При пересечении поверхности вращения многогранником их общим геометрическим элементом является некоторая линия.

Рассмотрим построение этой линии на примере решения задачи о пересечении прямой трехгранной призмы и сферы (рис. 6.6).

Рис. 6.6. Пересечение призмы и сферы.

Поскольку боковые грани призмы перпендикулярны к П ₁, то горизонтальная проекция линии пересечения призмы и сферы совпадает с горизонтальной проекцией призмы.

Остается построить фронтальную проекцию линии пересечения. Так как по двум проекциям геометрического объекта легко построить третью, то здесь мы ограничимся построением горизонтальной и фронтальной проекций.

Применим метод вспомогательных секущих плоскостей, в качестве которых выберем фронтальные плоскости уровня, проходящие через характерные (1, 3, 5) и промежуточные (2, 4) точки, лежащие на линии пересечения призмы и сферы. Их горизонтальные проекции 1₁, 2₁, 3₁, 4₁, 5₁ указаны на рис. 6.6.

Линией пересечения фронтальной плоскости уровня со сферой является окружность, для построения которой на П ₂ достаточно измерить расстояние от вертикальной оси до контура сферы на П _1, а затем этим радиусом на П ₂ провести окружность.

Рассмотрим построение фронтальной проекции какой-либо точки, например, точки 2. Проводим через нее фронтальную плоскость Ф*. Затем измеряем расстояние от точки 6₁ до 7₁ и этим радиусом проводим дугу окружности из точки О₂. Искомая точка лежит на пересечении этой дуги с линией связи, проведенной из точки 2₁. Аналогично строятся точки 1₂, 4₂, 5₂. Через точку 3 нет необходимости проводить вспомогательную секущую плоскость, так как она лежит на контуре сферы в проекции на П ₂, и для построения точки 3₂ достаточно провести из точки 3₁ линию связи до пересечения ее с контуром сферы.

Соединив точки 1₂, 2₂, 3₂, 4₂, 5₂, получаем один из участков искомой линии.

Так как участок линии между точками 5 и 8 лежит на фронтальной плоскости Ф***, что видно на его горизонтальной проекции 5₁8₁, то между точками 5₂ и 8₂ линия пересечения призмы и сферы представляет собой дугу окружности, проведенной через точку 5₂.

В связи с тем, что рассматриваемые поверхности симметричны относительно горизонтальной и профильной плоскостей уровня, искомая линия пересечения в проекции на П ₂ симметрична относительно вертикальной и горизонтальной осей, и ее построение не требует дополнительных пояснений.

Видимость линий определяется по видимости точек так же, как в предыдущих главах.

Используя метод вспомогательных секущих плоскостей, можно построить линию пересечения любых поверхностей вращения и многогранников. Если при построении линий пересечения вспомогательных секущих плоскостей и рассматриваемых поверхностей возникают затруднения, тогда необходимо способом замены плоскостей проекций получить проекции указанных поверхностей в более удобном виде.

6.4. Пересечение поверхностей вращения. Метод вспомогательных секущих концентрических сфер.

Оговоримся, что этот метод применим лишь в случае выполнения трех условий:

1. Обе поверхности, линию пересечения которых мы определяем, являются поверхностями вращения;

2. Их оси должны пересекаться;

3. Оси этих поверхностей вращения должны быть параллельны одной из плоскостей проекций.

Решим задачу о пересечении двух конусов, оси которых пересекаются и параллельны П ₂ (рис. 6.7).

Центром концентрических сфер, которые обеспечивают дополнительные построения, необходимые для решения задачи, является точка пересечения осей поверхностей вращения. В данном случае это точка О пересечения осей конусов.

Рассмотрим построение точек пересечения конусов с помощью произвольной сферы (рис. 6.7). Ее проекция на П₂ представляет собой окружность такого же радиуса, как и сфера.

А проекцией на П₂ линии пересечения построенной секущей сферы с конусом является прямая, параллельная основанию конуса. Ее можно построить, соединив точки пересечения окружности и контура конуса. Очевидно, что таких прямых две для каждого конуса.

Точки А ₂, В ₂, С ₂ пересечения этих прямых между собой и являются фронтальными проекциями точек пересечения конусов. Как видим, используя только одну окружность, можно получить несколько точек пересечения конусов. Ясно, что их не может быть более четырех для одной дополнительно построенной сферы.

Рис. 6.7. Построение точек пересечения конусов.

Далее не составляет труда построить горизонтальные проекции точек А, В, С, учитывая, что каждая из них является точкой на поверхности прямого конуса. Как излагалось ранее, для этого достаточно измерить расстояния от оси конуса до его контура по прямой, проходящей через точку, горизонтальную проекцию которой строим. Затем этим радиусом из точки О ₁ провести окружность и на ней по линии связи найти горизонтальную проекцию. На рис. 6.7 указанные построения выполнены для точки С. Поскольку ей на П₁ соответствует две точки С ₁ и С ₁*, то понятно, что на П₂ имеем дело с двумя конкурирующими точками. Поэтому, уточняя предыдущие замечания, следует отметить, что построенная секущая сфера дает не три, а шесть точек пересечения конусов. Построение горизонтальных проекций остальных точек ничем не отличается от вышеприведенного.

Для того, чтобы построить линию пересечения конусов, точек, через которые она проходит, должно быть достаточное количество. Дальнейшее решение поставленной задачи рассмотрим на рис. 6.8. Четыре точки 1₂, 2₂, 3₂, 4₂ имеем без дополнительных построений, так как они лежат на пересечении образующих конусов. Остальные точки на П ₂ получим, проведя четыре окружности. Для окружности радиуса R ₁ фронтальными проекциями точек пересечения конусов являются 5₂, 5₂*, 5₂**, 5₂***. Для окружности радиуса R ₂ таких точек две – 6₂, 6₂*. Окружность радиуса R ₃ дает также две точки - 7₂, 7₂*. Окружность радиуса R ₄ позволяет получить лишь одну точку 8₂. Очевидно, что проводить окружности радиусом, большим чем О ₂4₂, и меньшим, чем R ₂, не имеет смысла, так как не получим ни одной точки пересечения.

Рис. 6.8. Пересечение двух конических поверхностей.

Как видно на рис. 6.8, четырех окружностей достаточно для того, чтобы построить фронтальную проекцию линии пересечения конусов, соединив найденные точки.

Для построения горизонтальной проекции полученных точек необходимо решить рассмотренную ранее задачу построения точек на поверхности конуса. Так, для построения точки, например, 7₁ надо измерить расстояние по горизонтальной линии, проходящей через 7₂, от оси до контура конуса, а затем этим радиусом из точки О ₁ провести дугу. Точка 7₁ лежит на пересечении этой дуги с линией связи, проведенной из 7₂. Аналогично строятся горизонтальные проекции остальных точек.

Поскольку точки 5* и 5** лежат на образующей горизонтального конуса, которая на П ₁ является контурной, то, очевидно, что точки 5₁* и 5₁** служат точками перехода линии пересечения конусов из видимой зоны в невидимую.

С учетом того, что изображенные поверхности симметричны относительно фронтальной плоскости уровня, соединив построенные точки кривой линией, получим решение в окончательном виде (рис. 6.8).

6.5. Развертка цилиндра и конуса

Из всех поверхностей построение развертки возможно лишь для линейчатых поверхностей, образующей которых является прямая. К таковым относятся две – цилиндр и конус – из рассматриваемых нами поверхностей вращения. Развертку сферы и тора построить нельзя.

Дата добавления: 2015-06-30