Анализ ВВХ оборудования ЦОВ

Исследованиям центров обслуживания вызовов и, в частности, систем распределения вызовов посвящено множество публикаций. Несмотря на то, что СРВ — один из множества вопросов, требующих изучения в этой области, большинство авторов останавливает внимание именно на нем. Это объясняется тем, что СРВ является исторически первой и основной функцией контакт-центров, что дает возможность “отточить” на ней существующие научные методы исследований.

Для решения задач по расчету параметров систем распределения вызовов естественным образом приспособлена теория телетрафика, её методами и предполагается проводить дальнейшее изучение проблем обслуживания заявок, поступающих на контакт и Call-центры.

Библиография материалов, посвященных ЦОВ обширна. Подчиняясь одному стремлению — повысить эффективность работы строящихся операторских центров, области исследований варьируются от методов вычисления производительности ЦОВ средствами теории телетрафика до составления оптимальных программ работы персонала центра, динамического изменения его параметров в зависимости от поступающей нагрузки и влияния психологии пользователей на поступающую нагрузку.

Существующие материалы также могут быть разделены по уровню абстракции от реальных задач: одна часть работ выполняется с целью предоставить менеджменту существующих и будущих ЦОВ инструмент для планирования работы операторских центров, другая часть предназначается самим исследователям для дальнейшего продвижения в разработке механизмов расчетов ЦОВ, предсказания параметров их функционирования.

Из теории телетрафика известно, что системы массового обслуживания описываются при помощи классификации Кендалла, имеющей вид A/B/V/K/N.

Знак A характеризует процесс поступления вызовов, этот процесс описывается при помощи функции распределения промежутков между вызовами.

Знак B используется для описания процесса обслуживания вызовов, описывается функцией распределения длительности обслуживания.

V — число обслуживающих приборов или линий.

K — емкость накопителя, равная сумме числа обслуживающих приборов и мест в очереди.

N — число источников, создающих поток вызовов.

Если какой-либо из параметров классификации Кендалла является бесконечно большим, то используется соответствующий символ ¥, если данные параметры занимают последние места, то символ ¥ не указывается (например, при K = ¥ = N, используется запись вида A / B / V).

Если процесс A или B, или оба являются марковскими, то используется символ M: M / M / V — в данной модели процессы поступления и обслуживания вызовов являются марковскими (процесс без последействия, когда его будущее определяется только настоящим).

Если необходимо подчеркнуть произвольный закон распределения для того или иного процесса, то используется символ G, в случае детерминированного - D.

M/D/V - указывает на то, что длительность обслуживания является постоянной (неслучайной) величиной.

В зависимости от параметров задачи определения характеристик того или иного оборудования центров обслуживания вызовов, оно может быть представлено в виде различных моделей систем массового обслуживания, в том числе:

• СМО M/M/k/ ¥, M/M/k/N;
• СМО вида M₁ + … +M_c / M / k / N;
• СМО M/G/k/ ¥ или G/G/k/¥ с исследованием их поведения при вводе различных систем приоритетов для голосовых и текстовых сообщений;
• СМО с различными дисциплинами приоритетов поступающих на обслуживание заявок;
• СМО с распределениями времен обслуживания заявок и их поступления, отличными от экспоненциального (long-normal, PH).

Кратко остановимся на основных методах исследования центров обслуживания вызовов в соответствии с их эволюцией.

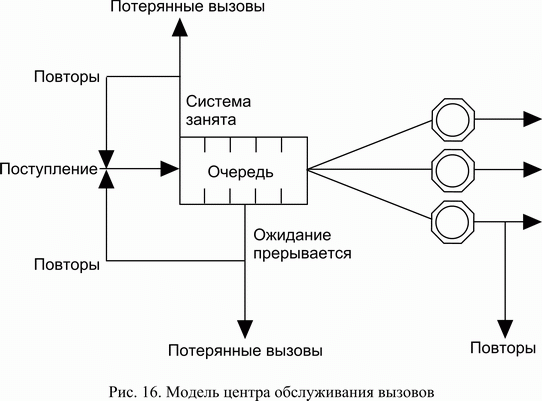
Вызовы (рис. 16) поступают на систему по входящим соединительным линиям от ТфОП и обрабатываются операторами, число которых меньше либо равно числу линий. В случае, если входящий вызов застает все линии занятыми, то он отклоняется, абоненту телефонной сети будет передан сигнал “занято”. Если свободные линии есть, то вызов поступает в систему, далее в зависимости от числа свободных операторов вызов может быть немедленно передан на обслуживание либо поставлен на ожидание. Часть вызовов может уйти из очереди, не дождавшись обслуживания. Для всех неуспешных (не окончившихся обслуживанием) вызовов возможны повторные попытки. Обслуженные вызовы могут уйти из системы или возвратиться в нее для дальнейшего обслуживания.

Наиболее простым способом моделирования call-центра является применение модели СМО типа M/M/k по классификации Кендалла, с неограниченным числом мест для ожидания. Несмотря на то, что подобная модель не принимает в расчет возможности потери вызовов из-за занятости линий, “нетерпеливости” пользователя, многоэтапного обслуживания и т. п., она является приемлемым средством оценки характеристик множества простых центров обслуживания вызовов.

Рассмотрим один из многочисленных примеров применения такой модели СМО для исследования характеристик call-центров (рис. 17).

Рис. 17. Диаграмма интенсивностей переходов СМО вида M/M/N

Рассматривается модель M/M/N со следующими характеристиками:

интенсивность поступления вызововl _n= l, n = 0, 1, 2,…;

интенсивность обслуживания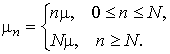

Для исследования характеристик центров обслуживания вызовов предлагается выбирать интервалы времени, на протяжении которых интенсивность поступления вызовов меняется незначительно (рис. 18).

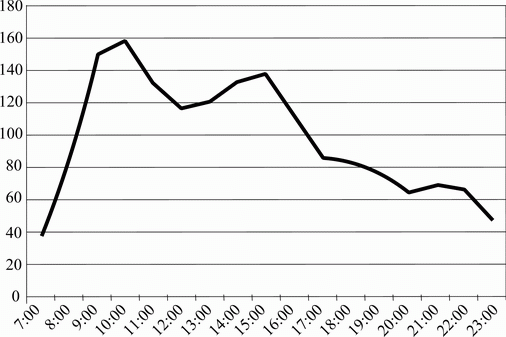
Рис. 18. Изменение во времени числа вызовов,
поступающих на один из существующих call-центров

Рассматриваемая система хорошо изучена, для неё известны следующие результаты. Если принять за l _i интенсивность поступления вызовов на временном интервале i, а за m _i = E [ S_i ]^–1 интенсивность обслуживания вызовов на данном интервале, то при 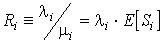, , где R_i — поступающая нагрузка, а p_i — коэффициент использования системы.

Для системы M/M/N известно выражение P {Wait > 0} = C (N, R_i), которое также называется С -формулой Эрланга или второй формулой Эрланга:

.
(1)

Среднее время ожидания обслуживания в такой системе

,
(2)

а доля пользователей, время ожидания для которых составит менее Т:

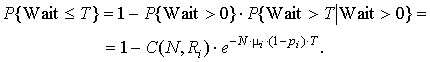
(3)

Экспериментальные данные (рис. 19) близки к получаемым из приведенных соотношений (1) – (3).

Рис. 19. Диаграмма зависимости времени ожидания от использования системы
и обслуживания вызова в простом call-центре

Однако при всем удобстве и простоте такого подхода, он, все-таки, не учитывает важных особенностей функционирования реальных центров обслуживания вызовов и, как следствие, может применяться только для поверхностной оценки исследуемых характеристик.

В ряде случаев, при исследовании центров обслуживания вызовов, можно столкнуться не с экспоненциальным временем обслуживания заявок.

Несмотря на неудобство применения модели СМО вида M/G/N, известно следующее приблизительное соотношение:

,
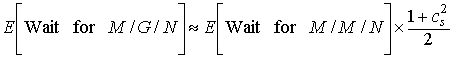(4)

где — коэффициент вариации, дисперсия s², S — время обслуживания.

В случае большой нагрузки на систему (С (N, R)» 1) — это выражение принимает вид:

.
(5)

Учесть возможность блокировки вызова, когда ему отказывается в обслуживании по причине отсутствия свободных линий, можно при помощи использования модели СМО вида M/M/N/N, для которой известна так называемая первая или B -формула Эрланга и которая описывает долю времени, когда все обслуживающие приборы системы заняты.

Диаграмма интенсивностей переходов для такой системы показана на рис. 20, а вероятность занятости всех обслуживающих приборов

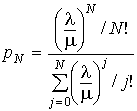
— первая или B-формула Эрланга. (6)

Рис. 20. Диаграмма интенсивностей переходов СМО вида M/M/N/N

Широкое распространение в программном обеспечении модулей предсказания поведения характеристик центров обслуживания вызовов получили модели СМО с ограниченным буферным пространством. Это объясняется их близостью к реалиям существующих операторских центров.

Рассмотрим одну из таких моделей — СМО M/M/m/B (рис. 21).Отметим, что модель M/M/m/B близка по своим свойствам к рассмотренной выше M/M/N/N, за исключением ограниченного числа мест для ожидания, при переполнении которого поступающие заявки начинают теряться. Предполагается, что B > m, так как в противном случае некоторые обслуживающие приборы никогда бы не занимались, и система функционировала бы как M/M/B/B.

Рис. 21. Диаграмма интенсивностей переходов СМО вида M / M / m / B

Для описываемой системы интенсивность поступления заявок

l _n = l, n = 0, 1, …, B –1, интенсивность обслуживания

Соотношение, определяющее вероятность заданного числа заявок в системе n

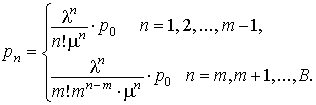
Определяя r = l / m · m, получаем

Используя известное равенство

,
(7)

можно найти p ₀.

Среднее число вызовов в очереди и среднее число вызовов в системе определяется следующими выражениями:

,
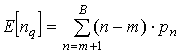(8)

.
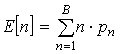(9)

Известно, что все вызовы, поступающие в систему, когда она находится в состоянии n = B, теряются.

Таким образом, действительная (эффективная) интенсивность поступления заявок в систему

,

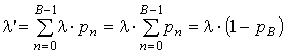где p_B — вероятность нахождения системы в состоянии B;

l - l' = p_B — интенсивность потерянных вызовов.

Отметим, что в данной модели заявки не могут быть потеряны после поступления в очередь.

Воспользуемся формулой Литтла для определения среднего времени ожидания обслуживания:

.
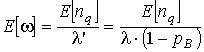(10)

Известно, что для модели M / M / m использование системы определяется по формуле , в случае ограниченного размера очереди

.
(11)

Перечисленные способы исследования характеристик операторских центров, несмотря на свою простоту, находят широкое применение в программном обеспечении оборудования ЦОВ.

Назад

Содержание

Вперед

Дата добавления: 2015-07-02