Если общий член ряда не стремится к нулю, то ряд расходится

Необходимый признак сходимости ряда

Я не буду записывать сам признак (его можно найти в любом учебнике), а сформулирую очевидное следствие:

Или короче: Если 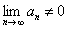, то ряд расходится.

В качестве «динамической» переменной вместо «икса» у нас выступает 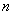. Букву можно заменить другой буквой, и это не страшно, однако есть разница с содержательной точки зрения. Освежим наши знания: пределы с «иксом» называют пределами функций, а пределы с переменной «эн» – пределами числовых последовательностей. Очевидное отличие состоит в том, что переменная «эн» принимает дискретные (прерывные) натуральные значения: 1, 2, 3 и т.д. Но данный факт мало сказывается на методах решения пределов и способах раскрытия неопределенностей.

Докажем, что ряд из первого примера 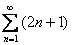расходится.
Общий член ряда: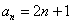

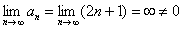
Вывод: ряд 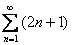расходится, так как не выполнен необходимый признак сходимости ряда.

Необходимый признак сходимости ряда довольно часто встречается в практических заданиях:

Пример 6

Исследовать ряд на сходимость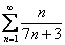

В числителе и знаменателе у нас находятся многочлены. Тот, кто внимательно прочитал и осмыслил метод раскрытия неопределенности в статье Пределы. Примеры решений, наверняка уловил, что когда старшие степени числителя и знаменателя равны, тогда предел равен конечному числу.

Решаем:

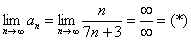
Делим числитель и знаменатель на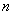

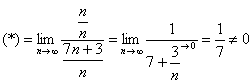
Исследуемый ряд расходится, так как не выполнен необходимый признак сходимости ряда.

Готово.

Пример 7

Исследовать ряд на сходимость

Это пример для самостоятельного решения. Полное решение и ответ в конце урока

Итак, когда нам дан ЛЮБОЙ ряд, в первую очередь проверяем (мысленно или на черновике): а стремится ли общий член к нулю? Если не стремится – оформляем решение по образцу примеров №№6,7 и даём ответ о том, что ряд расходится.

Какие типы очевидно расходящихся рядов мы рассмотрели? Сразу понятно, что расходятся ряды вроде 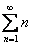или 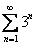. Также расходятся ряды из примеров №№6,7: когда в числителе и знаменателе находятся многочлены, и старшая степень числителя больше либо равна старшей степени знаменателя. Во всех этих случаях при решении и оформлении примеров мы используем необходимый признак сходимости ряда.

Почему признак называется необходимым? Потому-что, если общий член ряда стремится к нулю, ТО ЭТО ЕЩЕ НЕ ЗНАЧИТ, что ряд сходится. Или так: для того, чтобы ряд сходился, необходимо, чтобы его общий член стремился к нулю; но этого еще – не достаточно. Если общий член ряда стремится к нулю, то ряд может, как сходиться, так и расходиться! В таких случаях для решения примеров нужно использовать другие признаки.

Знакомьтесь:

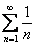
Данный ряд называется гармоническим рядом. Пожалуйста, запомните! Среди числовых рядов он является прима-балериной. Точнее, балеруном =)

Легко заметить, что , НО. В теории математического анализа доказано, что гармонический ряд расходится.

Также следует запомнить понятие обобщенного гармонического ряда:

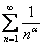
1) Данный ряд расходится при 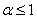. Например, расходятся ряды , , .
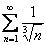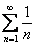2) Данный ряд сходится при . Например, сходятся ряды 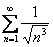, , 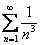. Еще раз подчеркиваю, что почти во всех практических заданиях нам совершенно не важно, чему равна сумма, например, ряда , важен сам факт его сходимости.

Это элементарные факты из теории рядов, которые уже доказаны, и при решении какого-нибудь практического примера можно смело ссылаться, например, на расходимость ряда или сходимость ряда .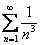

Дата добавления: 2015-07-02