Формальные определения

Информационная энтропия

11.

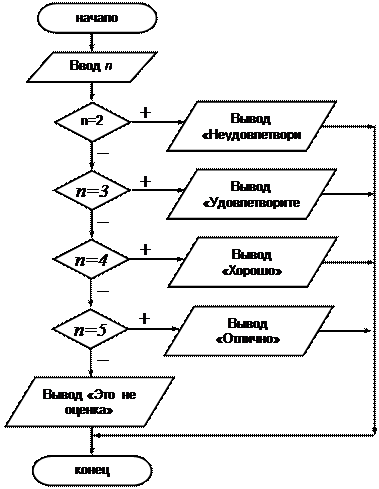12. Ответ: б

x = int(14/5)= 2

y = 2*5 + 5 mod 2 = 10+1=11

Содержание

1 Формальные определения

• 1.1 Определение по Шеннону
• 1.2 Определение с помощью собственной информации

2 Свойства

• 2.1 Математические свойства
• 2.2 Эффективность

3 Вариации и обобщения

• 3.1 b -арная энтропия
• 3.2 Условная энтропия
• 3.3 Взаимная энтропия

4 История

5 Примечания

6 См. также

7 Ссылки

8 Литература

Информацио́нная энтропи́я – мера неопределённости или непредсказуемости информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения.

Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределённость появления для некоторых букв меньше, чем для других. Если же учесть, что некоторые сочетания букв (в этом случае говорят об энтропии n -ого порядка, см. ниже) встречаются очень редко, то неопределённость ещё более уменьшается.

Энтропия – это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения.

Информационная двоичная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле:

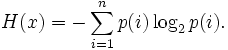
Эта величина также называется средней энтропией сообщения.

Величина p(i) – относительная частота появления события i.

Величина 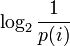называется частной энтропией, характеризующей только i -e состояние.

Таким образом, энтропия события x является суммой (с противоположным знаком) всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы^[1]. Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.

Дата добавления: 2015-07-02