Условная энтропия

B-арная энтропия

Вариации и обобщения

В общем случае b -арная энтропия (где b равно 2, 3, в) источника 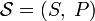с исходным алфавитом и дискретным распределением вероятности 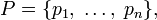где p_i является вероятностью a_i (p_i = p (a_i)), определяется формулой:

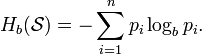
Если следование символов алфавита не независимо (например, во французском языке после буквы «q» почти всегда следует «u», а после слова «передовик» в советских газетах обычно следовало слово «производства» или «труда»), количество информации, которую несёт последовательность таких символов (а, следовательно, и энтропия), очевидно, меньше. Для учёта таких фактов используется условная энтропия.

Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (то есть, вероятности двухбуквенных сочетаний):

где i в это состояние, зависящее от предшествующего символа, и p_i (j) в это вероятность j при условии, что i был предыдущим символом.

Например, для русского языка без буквы «ё» ^[3].

Через частную и общую условные энтропии полностью описываются информационные потери при передаче данных в канале с помехами. Для этого применяются так называемые канальные матрицы. Для описания потерь со стороны источника (то есть известен посланный сигнал) рассматривают условную вероятность 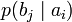получения приёмником символа b_j при условии, что был отправлен символ a_i. При этом канальная матрица имеет следующий вид:

	b 1	b 2	в	bj	в	bm
a 1		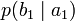	в		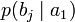в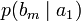
a 2		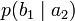	в		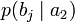в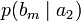
в	в	в	в	в	в	в
ai		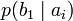	в		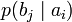в
в	в	в	в	в	в	в
am			в		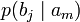в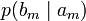

Очевидно, вероятности, расположенные по диагонали, описывают вероятность правильного приёма, а сумма всех элементов столбца даёт вероятность появления соответствующего символа на стороне приёмника в p (b_j). Потери, приходящиеся на передаваемый сигнал a_i, описываются через частную условную энтропию:

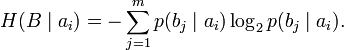
Для вычисления потерь при передаче всех сигналов используется общая условная энтропия:

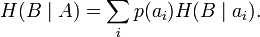
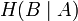означает энтропию со стороны источника, аналогично рассматривается 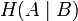в энтропия со стороны приёмника: вместо 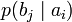всюду указывается 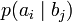(суммируя элементы строки можно получить p (a_i), а элементы диагонали означают вероятность того, что был отправлен именно тот символ, который получен, то есть вероятность правильной передачи).

Дата добавления: 2015-07-02