Прогнозирование на основе регрессионных моделей

Следующая прикладная задача корреляционно-регрессионного анализа – прогнозирование поведения признака-результата при том или ином изменении аргументов. Зная механизм влияния конкретных факторов на результат (имея регрессионную модель) и задавая возможные (желаемые) значения этих факторов, можно получить, так называемый, точечный прогноз значений исследуемого признака.

Регрессионная модель является, в известной мере, абстракцией, превращающей корреляционную зависимость между признаками в функциональную. Ожидаемые средние значения результативного признака полностью определяются конкретными значениями независимых переменных, при таком условии теоретическая линия регрессии должна пройти через все эмпирические точки, чего, безусловно, быть не может. Поэтому, точечный прогноз, полученный на основе выбранной модели связи, дополняется расчетом доверительных интервалов для математического ожидания отклика.

Величина ошибки прогноза и, следовательно, доверительный интервал зависят от амплитуды колебаний фактических значений вокруг линии регрессии (среднеквадратической ошибки), от объема выборочной совокупности и от значения переменной , с учетом которого прогнозируется величина признака-результата . Чем меньше отличается от , тем меньше ошибка прогноза. Предельная ошибка прогноза рассчитываются следующим образом:

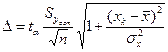, (6.1)

где ,

k – число факторов, включенных в уравнение регрессии;

- коэффициент доверия, величина которого определяется исходя из удовлетворяющего исследователя уровня вероятности, по таблице t-распределения Стьюдента, при d.f.=n-k-1;

х_k –заданное значение признака-фактора.

На основании точечного прогноза величины результативного признака (), с учетом предельной ошибки определяется доверительный интервал прогноза:

(6.2)

Т.о., с определенной вероятностью можно утверждать, что при заданном значении аргумента, математическое ожидание признака-результата будет находиться в указанных границах.

Применяя регрессионную модель для прогнозирования, необходимо учитывать только допустимые значения независимой переменной. Диапазон таких значений ограничивается размахом вариации признака-фактора. Иными словами, предсказывая значения результативного признака, можно выполнить только интерполяцию в пределах возможных значений аргумента, экстраполяция значений невозможна.

Дата добавления: 2015-07-02