Анализ парной корреляционной зависимости

При построении поля корреляции программа строит и линейное уравнение регрессии. Однако на практике мы не всегда имеем дело с линейной зависимостью и на основе поля корреляции не всегда очевиден вид связи между анализируемыми переменными. Поэтому, как правило, строят несколько уравнений регрессии и на основе описанных выше критериев выбирают модель, наилучшим образом отражающую корреляционную связь х и у.

Построим и сравним, например, линейную, степенную и экспоненциальные регрессионные модели.

Для построения моделей линейного типа (парных, множественных или линеаризованных) удобно воспользоваться меню Statistics/Multiple Regression (рис. 7.12.)

Рис. 7.12. Запуск процедуры Statistics/Multiple Regression.

В появившемся окне нажимаем на кнопку выбора переменных Variables (рис. 7.13). В левое поле (Dependent variable) выбираем «Y» (зависимая переменная, результат), а в правое поле (Independent variable) выбираем соответственно «Х» (независимая переменная, фактор) (рис. 7.14.).

Рис. 7.13. Внешний вид процедуры Statistics/Multiple Regression.

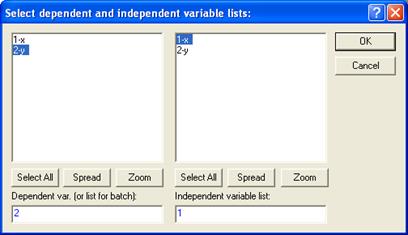
Рис. 7.14. Окно выбора переменных.

Далее нажимаем ОК. Появляется диалоговое окно, в верхнем поле которого даны основные показатели уравнения, такие как 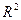- коэффициент детерминации, F – критерий Фишера (рис. 7.15.). Переходим на закладку Advanced (рис. 7.16.).

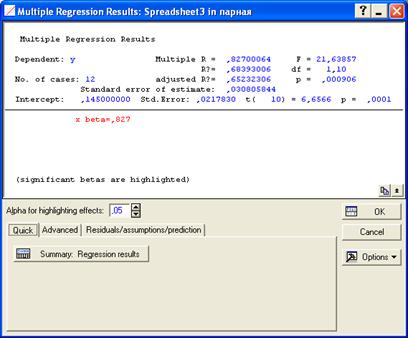
Рис. 7.15. Закладка Quick процедуры Multiple Regression Results.

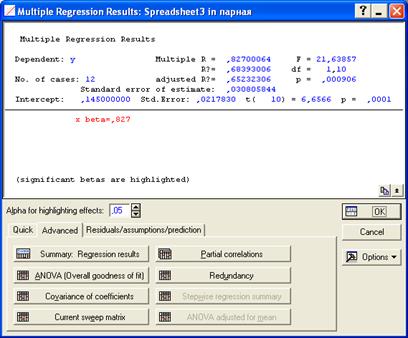
Рис. 7.16. Закладка Advanced процедуры Multiple Regression Results.

Вверху нижней части модуля в поле Alpha for highlighting effects задается теоретический уровень значимости (0,05). Далее расположены закладки и кнопки с различными функциями.

В первую очередь нас интересует кнопка Summary: Regression Results. При нажатии на нее получаем две таблицы с результатами регрессионного анализа. В первой (рис. 7.17.) представлены результаты расчета параметров уравнения регрессии, во второй (рис. 7.18.) – основные оценочные показатели уравнения и показатели корреляции.

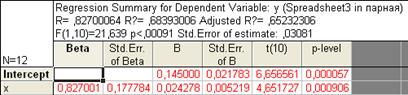
Рис. 7.17. Результаты расчета параметров уравнения линейной регрессии.

Здесь N = 12 – объем изучаемой совокупности. В верхнем поле расположены показатели R, 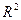, Adjusted R, F, p, Std.Error of Estimate, означающие соответственно: теоретическое корреляционное отношение, коэффициент детерминации, скорректированный коэффициент детерминации, расчетное значение критерия Фишера (в скобках дано число степеней свободы факторной и остаточной дисперсий), уровень значимости, стандартная ошибка уравнения (эти же показатели можно увидеть в таблице на рис. 7.18.). В самой таблице нас интересуют столбцы: В - параметры уравнения; t и p-level, содержащие расчетные значения t-критерия и уровня значимости, необходимые для оценки статистической значимости параметров уравнения. При этом система помогает пользователю: когда процедура предполагает проверку на значимость, STATISTICA выделяет значимые элементы красным цветом (т.е. отвергается нулевая гипотеза о равенстве параметров нулю). В нашем случае |t_факт| > t_табл (2,228) для обоих параметров, следовательно они значимы.

Соответственно уравнение линейной регрессии выглядит следующим образом:

.

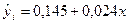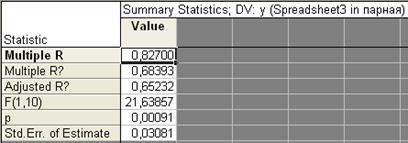
Рис. 7.18. Показатели корреляции и оценка линейного уравнения регрессии.

Кнопка ANOVA (Overall goodness of fit) которая находится на той же закладке Advanced (рис. 7.16.) позволяет получит результаты дисперсионного анализа (рис. 7.19.).

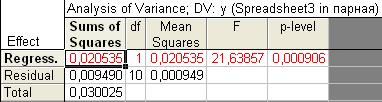
Рис. 7.19. Результаты дисперсионного анализа линейного уравнения регрессии.

Sums of Squares – сумма квадратов отклонений: на пересечении со строкой Regression – сумма квадратов отклонений теоретических (полученных по уравнению регрессии) значений признака от средней величины. Эта сумма квадратов используется для расчета факторной, объясненной дисперсии зависимой переменной. На пересечении со строкой Residual – сумма квадратов отклонений теоретических и фактических значений «» (для расчета остаточной, необъясненной дисперсии), Total – отклонений фактических значений от средней величины (для расчета общей дисперсии). Столбец df – число степеней свободы, Means Squares обозначает дисперсию: на пересечении со строкой Regression – факторную, со строкой Residual - остаточную, F – критерий Фишера, используемый для оценки общей значимости уравнения и коэффициента детерминации, p-level – уровень значимости F – критерия.

Фактическая величина критерия сравнивается с его теоретическим (табличным) значением исходя из соответствующего числа степеней свободы и заданного уровня значимости. Если F _факт.> F _теор., то можно считать, что уравнение в целом значимо.

В нашем случае теоретическое значение критерия Фишера равно 4,96, следовательно, уравнение в целом и коэффициент детерминации статистически значимы.

Далее построим графическое изображение линии регрессии, наложенное на корреляционное поле, с 95% доверительными интервалами. Для этого переходим на закладку Residuals/Assumptions/Prediction и нажимаем кнопку Perform residual analysis (рис. 7.20.). В появившемся окне анализа остатков Residual Analysis переходим на закладку Scatterplots (рис. 7.21.). Находясь на закладке Scatterplots, нажимаем на кнопку Predicted vs. Observed (рис. 7.22.). Это означает, что линия регрессии (сплошная) наносится на корреляционное поле, полученное с помощью фактическихзначений с 95% доверительными интервалами (пунктирные линии) (рис. 7.23.).

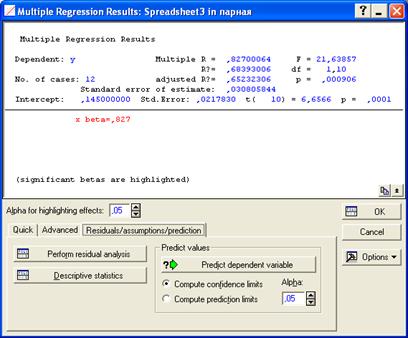
Рис. 7.20. Закладка Residuals/Assumptions/Prediction процедуры

Multiple Regression Results.

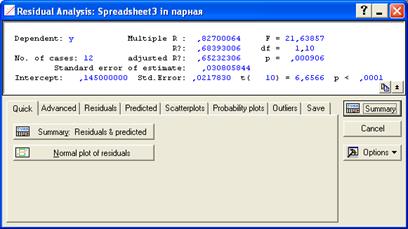
Рис. 7.21. Закладка Quick процедуры Residual Analysis.

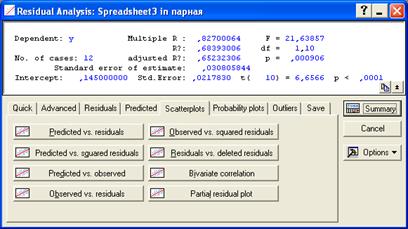
Рис. 7.22. Закладка Scatterplots процедуры Residual Analysis.

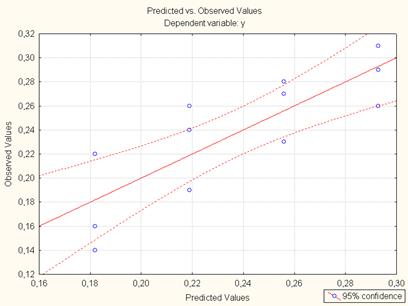
Рис. 7.23. Корреляционное поле и линия регрессии с нанесенными 95 – процентными доверительными интервалами. для линейной модели.

Далее рассмотрим другую процедуру, позволяющую строить регрессионные модели как линейного, так и нелинейного типа.

Для этого выбираем: Statistics/Advanced Linear/Nonlinear Models/Nonlinear Estimation/ (рис. 7.24.).

Рис. 7.24. Запуск процедуры Statistics/Advanced Linear/Nonlinear Models/Nonlinear Estimation.

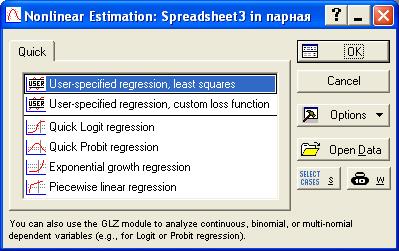
Рис. 7.25. Вид окна процедуры Nonlinear Estimation.

В появившемся окне (рис. 7.25.) выбираем функцию User-specified Regression, Least Squares (построение моделей регрессии пользователем вручную, параметры уравнения находятся по М.Н.К.).

Рис. 7.26. Вид окна процедуры User-Specified Regression, Least Squares. В следующем диалоговом окне (рис. 7.26.) нажимаем на кнопку Function to be estimated, чтобы попасть на экран для задания модели вручную (рис. 7.27.).

Рис. 7.27. Окно для реализации процедуры задания вручную уравнения регрессии.

В верхней части экрана находится поле для ввода функции, в нижней части располагаются примеры ввода функций для различных ситуаций.

Прежде чем сформировать интересующие нас модели, необходимо пояснить некоторые условные обозначения. Переменные уравнений задаются в формате «v№», где «v» обозначает переменную (от англ. «variable»), а «№» - номер столбца, в котором она расположена в таблице на рабочем листе с исходными данными. Если переменных очень много, то справа находится кнопка Variables, позволяющая выбирать их из списка по названиям и просматривать их параметры (рис.8, кнопка Zoom).

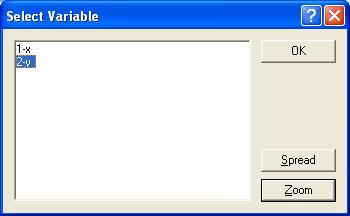
Рис. 7.28. Вид окна ввода переменной.

Параметры уравнений задаются любыми латинскими буквами, не обозначающими какое-либо математическое действие. Для упрощения работы предлагается обозначать параметры уравнения как в теоретическом разделе данного пособия, то есть через латинские буквы «а», последовательно присваивая им порядковые номера. Знаки математических действий (вычитания, сложения, умножения и прочие) задаются в обычном для Windows приложений формате. Пробелы между элементами уравнения не требуются.

Итак, построим степенную функцию для нашего примера. Степенная функция имеет вид: 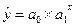, следовательно после набора она будет выглядеть:

,

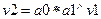где v2 – это столбец на листе с исходными данными, в котором находятся значения признака-результата,

а0 и а1 – параметры уравнения,

v1 - столбец на листе с исходными данными, в котором находятся значения признака-фактора (рис. 7.29.).

После этого дважды нажимаем кнопку ОК. (рис. 7.30.).

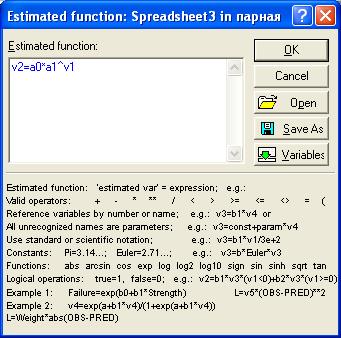
Рис. 7.29. Вид окна процедуры задания уравнения степенной модели регрессии.

Рис. 7.30. Вид окна процедуры User-Specified Regression с выбранной степенной функцией.

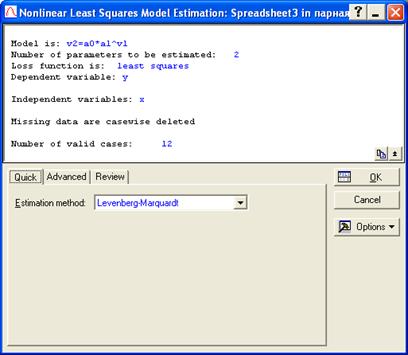
Рис. 7.31. Закладка Quick процедуры оценки уравнения регрессии.

В появившемся окне (рис. 7.31) можно выбрать метод оценки параметров уравнения регрессии (Estimation Method), если это необходимо. В нашем случае нужно перейти к закладке Advanced и нажать на кнопку Start Values: (рис. 7.32). В этом диалоге задаются стартовые значения параметров уравнения для их нахождения по М.Н.К., то есть их минимальные значения. Изначально они заданы как 0,1 для всех параметров. В нашем случае поставим стартовые значения, равные одной тысячной для обоих параметров, так как значения в наших исходных данных меньше единицы (рис. 7.33.). Нажимаем кнопку ОК.

.

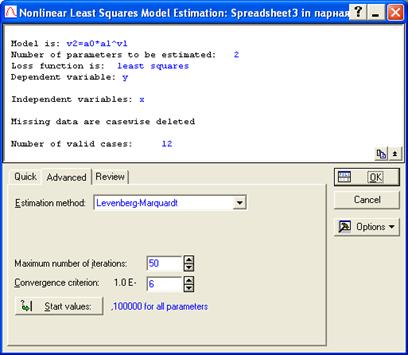
Рис. 7.32. Закладка ?????Quick процедуры оценки уравнения регрессии.

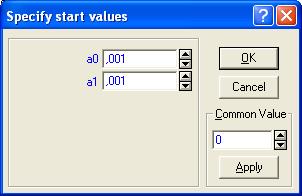
Рис. 7.33. Окно задания минимальныхзначений

параметров уравнения.

Рис. 7.34. Закладка Quick окна результатов регрессионного анализа.

На закладке Quick (рис. 7.34.) нажимаем кнопку Summary: Parameter estimates для построения степенной модели регрессии.

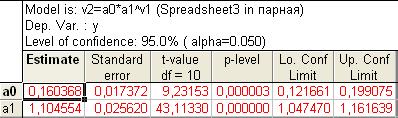
Рис. 7.35. Результаты расчета параметров степенной модели.

Соответственно уравнение степенной модели регрессии имеет вид .

В таблице (рис. 7.35.) столбец Estimate – численные значения параметров уравнения, Standard еrror – стандартная ошибка параметра, t-value – расчетное значение t-критерия, df – число степеней свободы (n-2), p-level – расчетный уровень значимости, Lo. Conf. Limit и Up. Conf. Limit – соответственно нижняя и верхняя граница доверительных интервалов для параметров уравнения с установленной вероятностью (указана как Level of Confidence в левом поле таблицы).

После этого нажимаем на кнопку Analysis of Variance (дисперсионный анализ) на той же закладке Quick (рис. 7.34.). В основном содержание появившейся таблицы (рис. 7.36.) аналогично описанной выше (см. комментарии к рис). рассчитаны следующие показатели: Sum of Squares – сумма квадратов для расчета дисперсий (подробнее см. выше): на пересечении со строкой Regression – сумма квадратов теоретических (полученных по уравнению регрессии) значений признака. На пересечении со строкой Residual – сумма квадратов отклонений теоретических и фактических значений «» (для расчета остаточной, необъясненной дисперсии), Total – сумма квадратов фактических значений . Столбец df – число степеней свободы, Means Squares обозначает: на пересечении со строкой Regression – сумма квадратов прогнозных значений, деленное нп число степеней свободы, со строкой Residual - остаточную, F – критерий Фишера, используемый для оценки общей значимости уравнения и коэффициента детерминации, p-level – уровень значимости.

Две новые строчки (Corrected Total,Regression vs. Corrected Total) содержат результат корректировки соответствующих характеристик с учетом числа степеней свободы.

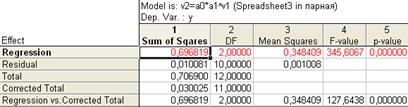
Рис. 7.36. Дисперсионный анализ степенной модели.

Исходя из данных таблицы, легко найти коэффициент детерминации R²(ή²), как квадрат теоретического корреляционного отношения, представляющий собой долю факторной (объясненной) дисперсии в общей дисперсии признака-результата. В столбце Sum of Squares строчка Corrected Total - это общая дисперсия, вычитая из нее величину остаточной дисперсии - строчка Residual, получаем факторную дисперсию, отсюда:

.

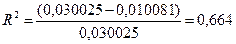Ту же величину можно получить, используя формулу индекса корреляции:

Далее переходим к закладке Advanced (рис. 7.37.). Здесь имеется возможность задавать уровень значимости (p-level for highlighting) и вероятность расчета доверительных интервалов для параметров уравнения (Confidence intervals for parameter estimates).

Кнопка Fitted 2D function & observed vals. позволяет вывести графическое изображение линии регрессии на корреляционном поле, правда без отображения доверительных интервалов (рис. 7.38.).

На закладке Residuals можно воспользоваться кнопкой Predicted vs. Observed, которая позволит построить поле корреляции, полученное с помощью фактических и прогнозных значений, но без линии регрессии.

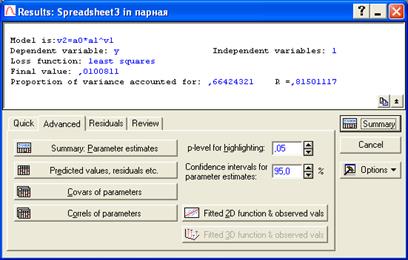
Рис. 7.37. Закладка Advanced результатов регрессионного анализа.

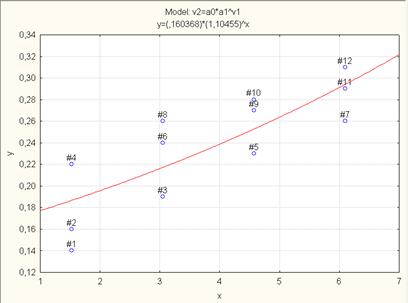
Рис. 7.38. Корреляционное поле с наложением линии степенной регрессии.

Теперь сделаем то же самое для экспоненциальной модели (рис. 7.39 – 7.42).

Рис. 7.39. Вид окна процедуры задания уравнения

экспоненциальной модели регрессии.

Рис. 7.40. Результаты расчета параметров экспоненциальной модели.

Соответственно уравнение экспоненциальной модели регрессии имеет вид .

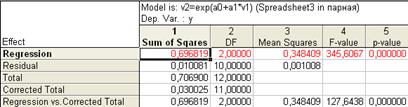
Рис. 7.41. Дисперсионный анализ экспоненциальной модели.

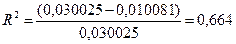
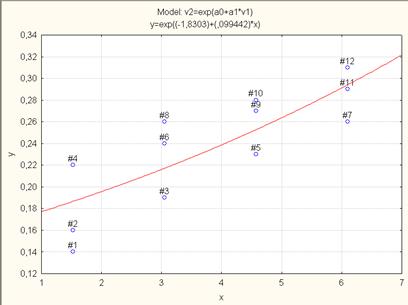
Рис. 7.42. Корреляционное поле и кривая экспоненциальной регрессионной модели.

Выбор лучшей модели можно осуществить исходя из значений коэффициента детерминации, либо остаточной дисперсии. Процедуру можно представить в виде следующей таблицы:

Таблица 7.3

Итоговая таблица уравнений и показателей регрессионного анализа.

№	Модель	Уравнение	R^2(ή^2)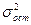
	Линейная		68,4%	0,00095
	Степенная		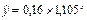66,4%	0,001
	Экспоненциальная		66,4%	0,001

Т.о., лучшей регрессионной моделью можно считать линейную, так как ей соответствует максимальное значение коэффициента детерминации, а остаточная дисперсия минимальна. Уравнение в целом по F- критерию Фишера (см. выше) значимо. Параметры уравнения также статистически значимы, поскольку t-статистика по модулю превышает 2, 228 (табличное значение).

Для расчета доверительных интервалов параметров уравнения воспользуемся величинами среднеквадратических ошибок параметров – S (графа Std.Error of В в таблице уравнения регрессии линейной модели).

,

,

,

,

.

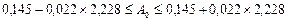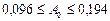
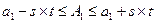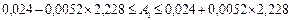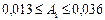Величина коэффициента доверия (t) определяется по таблице распределения Стьюдента (Приложение 3) исходя из доверительной вероятности (95%) и числа степеней свободы (n- k-1), где n – число наблюдений, k – число признаков-факторов в уравнении.

Дата добавления: 2015-07-02