Множественный корреляционный анализ

Зависимости

Изучение множественной корреляционной

Изучение множественной корреляционной зависимости предполагает оценку влияния на результативный признак двух и более факторов. При этом рассчитываются множественные (совокупные) и частные коэффициента корреляции, которые можно определить на основе парных коэффициентов корреляции ().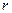

Так, при двухфакторной модели связи рекуррентная формула множественного коэффициента корреляции выглядит следующим образом:

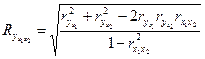. (5.1)

Значения R изменяются в пределах от 0 до 1. Величина совокупного коэффициента корреляции всегда больше любого из парных коэффициентов и включение в анализ новых факторов не может привести к уменьшению значения R.

Квадрат множественного коэффициента корреляции (R²) является множественным коэффициентом детерминации и характеризует долю дисперсии результативного признака, объясненную вариацией всех факторов, включённых в анализ, в общей дисперсии результата.

При небольших объёмах выборки увеличение числа объясняющих переменных приводит к существенному завышению значений совокупных показателей тесноты связи. Поэтому, если 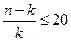(k – число объясняющих переменных), множественный коэффициент детерминации необходимо скорректировать на потерю числа степеней свободы вариации:

. (5.2)

Скорректированный коэффициент детерминации всегда меньше нескорректированного. На основе скорректированного коэффициента проводят сравнение степени объяснённости вариации результативного признака моделями, содержащими разное число факторов.

При изучении множественной корреляционной зависимости наряду с оценкой совокупного влияния всего набора интересующих исследователя факторов, возникает необходимость получить количественную характеристику влияния каждой объясняющей переменной, очищенную от опосредованного воздействия других факторов. Эта задача решается с помощью так называемых частных (парциальных) коэффициентов корреляции. При их построении применяется приём элиминирования влияния всех факторов кроме фактора, оцениваемого в данный момент. Элиминирование осуществляется путем закрепления значений признаков-факторов на неизменном (среднем) уровне. Таким образом, частные коэффициенты корреляции позволяют измерить "очищенное" влияние конкретного фактора.

Частные коэффициенты так же могут быть рассчитаны по рекуррентной формуле. Если элиминируется влияние одного фактора, то частный коэффициент корреляции называется коэффициентом первого порядка и в условиях двухфакторной модели рассчитывается:

, (5.3)

где - частный коэффициент корреляции первого порядка. Точка между х₁ и х₂ означает, что элиминируется влияние х₂.

Если элиминируется влияние фактора х₁, то частный коэффициент корреляции рассчитывается следующим образом:

. (5.4)

На основе частных коэффициентов первого порядка рассчитываются частные коэффициенты второго порядка, которые в свою очередь служат базой для расчёта коэффициентов третьего порядка и т.д.

Квадрат частного коэффициента корреляции - это частный коэффициент детерминации. Он характеризует долю дисперсии результативного признака, объясняемую дополнительно при включении в анализ конкретного фактора, в дисперсии результата, необъяснённой ранее включёнными в анализ факторами. Величина частных коэффициентов детерминации позволяет ответить на вопрос о необходимости дополнительного включения в анализ того или иного фактора.

Дата добавления: 2015-07-02