Корреляционный анализ

Изучение парной корреляционной зависимости

Методы выявления корреляционной зависимости

Статистическими приёмами, позволяющими выявить или опровергнуть наличие корреляционной зависимости между анализируемыми признаками, являются:

1. Построение и анализ параллельных рядов. При этом строится ранжированный ряд значений факторного признака и параллельно – ряд соответствующих значений признака-результата. По согласованному или несогласованному изменению значений фактора и результата судят о наличии либо отсутствии зависимости.

2. Построение и анализ групповых таблиц. Групповая таблица строится по правилам аналитической группировки. В качестве группировочного признака используется факторный признак. По каждой из выделенных групп рассчитывается среднее значение результативного признака. Наличие закономерности в изменении средних величин зависимой переменной будет свидетельствовать о присутствии корреляционной связи.

3. Построение и анализ корреляционных таблиц. В отличие от групповых, построение корреляционных таблиц предполагает группировку данных и по признаку-фактору, и по признаку-результату. На пересечении строк и столбцов проставляются частоты, то есть число единиц совокупности с данным сочетанием уровней изучаемых признаков. Характер расположения частот на поле таблицы позволяет выдвинуть предположение о наличии и направлении зависимости между признаками.

4. Графический метод. Этот метод наиболее часто используется на практике. В прямоугольной системе координат по оси абсцисс откладываются значения признака-фактора, а по оси ординат – значения результативного признака. Точки на графике соответствуют единицам совокупности с конкретными сочетаниями значений признаков. Получаемый точечный график называют "полем корреляции". По расположению точек на графике судят о наличии или отсутствии зависимости, а также о направлении и степени тесноты корреляционной связи.

Перечисленные методы подробно описаны в учебной литературе.

Выше были названы практические цели изучения связей. Остановимся на методах их реализации.

При необходимости определить круг факторов, влияющих на признак-результат (объект управления), оценить степень их влияния, рассчитывают показатели корреляции и детерминации.

Исторически первой и простейшей характеристикой тесноты связи является линейный коэффициент парной корреляции. Он используется при изучении парной корреляционной зависимости, то есть когда оценивается связь между парой признаков. Безусловно, невозможно назвать социально-экономические явления или процессы, развитие которых обусловлено лишь одним фактором. Но на практике часто возникает необходимость оценить тесноту связи результативного признака (объекта управления) с каким-либо конкретным фактором.

Показатели корреляции основаны на оценке сопряженной вариации изучаемых признаков. Парный коэффициент корреляции (r) – это нормированный коэффициент ковариации. Ковариация, являясь мерой взаимосвязи двух переменных, рассчитывается как средняя величина произведения отклонений индивидуальных значений анализируемых признаков от их средних значений:

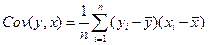(4.1)

Недостаток этого показателя (численное значение ковариации зависит от размерности переменных x и y) преодолевается в парном коэффициенте корреляции, путем нормирования абсолютных отклонений.

и ,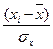

где σ _y - среднее квадратическое отклонение признака-результата;

σ _x - среднее квадратическое отклонение признака-фактора;

Парный коэффициент корреляции определяется:

, (4.2)

где n – число единиц в статистической совокупности.

Можно привести иную транскрипцию формулы линейного коэффициента корреляции Пирсона, часто встречающуюся в учебной и профессиональной литературе:

(4.3)

или

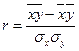(4.4)

Коэффициент корреляции изменяется в пределах:

0 ≤ |r| ≤ 1.

Если r = 0, линейная связь между изучаемыми признаками отсутствует. Если |r| = 1, связь функциональная, то есть значение зависимой переменной полностью определяется независимой переменной. Положительная величина коэффициента свидетельствует о прямой зависимости между признаками, отрицательная – об обратной.

Использование статистических методов анализа часто базируется на данных выборочного наблюдения. Как известно, с уменьшением объёма выборки снижается надёжность статистических характеристик, в том числе и коэффициента корреляции. Поэтому возникает вопрос, достаточна ли величина r, чтобы вывод о наличии корреляционной связи между изучаемыми признаками считать обоснованным. Иными словами, необходимо доказать, что значение коэффициента корреляции сформировано под влиянием неслучайных факторов, то есть значение r статистически значимо.

С этой целью проверяется нулевая гипотеза о равенстве генерального коэффициента корреляции нулю:

H_o: = 0,

где -генеральный коэффициент корреляции.\

Исходя из того, что дисперсия 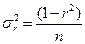, t–статистика для проверки H_o рассчитывается по следующей формуле:

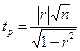(4.5)

Расчётное значение t–статистики сравнивается с табличным значением. Если t _p > t _табл, то нулевая гипотеза отвергается с вероятностью ошибки α (в социально-экономических исследованиях чаще всего α = 0,05 (1-0,95) или α = 0,01(1-0,99)). Другими словами признаётся, что величина r статистически значима.

В условиях малой выборки, при справедливости H_o, t-статистика имеет распределение Стьюдента. t-статистика в данном случае рассчитывается по формуле:

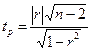(4.6)

Входными параметрами для отыскания табличного значения являются: α (0.05; 0.01) и числом степеней свободы d.f. = n – 2.

Следует иметь в виду, что если 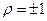, то частотное распределение оказывается вырожденным, поскольку в этих случаях 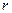не отличается от точного значения . При 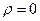, выборочное распределение 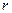является симметричным, а статистический критерий 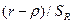хорошо аппроксимируется t-распределением. Наконец, когда имеет значение, близкое к 1, распределение оказывается резко асимметричным .[Э. Кейн, с. 46] Учитывая сложность распределения , при определении доверительных интервалов для коэффициента корреляции используют z - преобразование Р.Фишера [ ], доказавшего, что распределение логарифмической функции линейного коэффициента корреляции 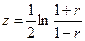, даже в условиях малой выборки соответствует нормальному закону распределения со средней, равной 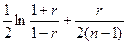и дисперсией .

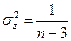Таблицы 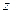- преобразования Фишера (Приложение 1), позволяют по величине коэффициента корреляции определить значение z и наоборот.

Доверительные границы для z рассчитываются:

, (4.7)

где z' – табличное значение z, соответствующее величине выборочного r;

t – коэффициент доверия, определяемый по таблице нормального распределения и соответствующий уровню доверительной вероятности, задаваемому исследователем.

Затем выполняется обратная процедура. Пользуясь таблицами Р.Фишера, находят доверительные границы для коэффициента корреляции.

Парный коэффициент корреляции – это симметричная характеристика, то есть r_yx = r_xy. Значение r отражает только степень тесноты корреляционной связи между изучаемыми признаками, но не свидетельствует о причинно-следственной зависимости между ними. Обоснование наличия причинно-следственной связи между признаками опирается на положения экономической теории, на анализ природы изучаемого явления.

Квадрат коэффициента корреляции (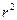) называется коэффициентом детерминации. Его величина изменяется в пределах от 0 до 1, и означает долю вариации результативного признака, обусловленную вариацией признака-фактора.

Парный коэффициент корреляции достаточно точно оценивает тесноту связи в условиях линейной зависимости между изучаемыми признаками. При наличии нелинейной связи он может привести к неверным выводам о степени тесноты связи (его величина занижена), поэтому в случае нелинейной зависимости корректнее использовать такой универсальный показатель, как корреляционное отношение (η).

Корреляционное отношение η может быть рассчитано на основе аналитической группировки, так называемое эмпирическое корреляционное отношение, а также по результатам регрессионного анализа - теоретическое корреляционное отношение.

Расчёт корреляционного отношения основан на правиле сложения дисперсий: общая дисперсия результативного признака – это сумма факторной (объяснённой) дисперсии и остаточной (необъяснённой) дисперсии.

В терминах аналитической группировки: общая дисперсия () признака-результата равна сумме межгрупповой () и средней из внутригрупповых дисперсий ().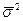

Общая дисперсия результативного признака формируется под влиянием всех мыслимых и не мыслимых (не известных исследователю) факторов. Среди них, естественно, есть и факторы, включенные в регрессионную модель.

Межгрупповая дисперсия – это дисперсия результативного признака, обусловленная вариацией группировочного признака, то есть признака-фактора, включенного в модель (аналог факторной дисперсии). В иных терминах эта составляющая общей дисперсии называется объясненной дисперсией, т.е. это часть общей дисперсии, объясненная воздействием фактора (факторов), включенных в регрессионную модель.

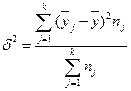, (4.8)

где 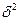- межгрупповая дисперсия;

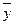- среднее значение признака-результата в изучаемой совокупности;

- среднее значение признака-результата в j-й группе;

- число единиц в j-й группе;

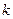- число выделенных групп.

Внутригрупповая дисперсия – это дисперсия результативного признака, обусловленная вариацией прочих факторов, не включенных в модель (аналог остаточной дисперсии), иными словами это необъясненная (факторами, включенными в модель) часть общей дисперсии. По совокупности в целом она определяется как средняя величина из дисперсий признака в каждой выделенной группе:

, (4.9)

где - дисперсия результативного признака в j-й группе;

-­­­­­­значение признака у i-й единицы j-й группы;

-среднее значение внутригрупповых дисперсий.

Таким образом,

.

Эмпирическое корреляционное отношение представляет собой:

или 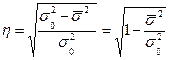(4.10)

η – изменяется от 0 до 1. Следует особо подчеркнуть, что кореляционное отношение знака не имеет. Чем ближе значение корреляционного отношения к 1, тем теснее связь между признаками, при функциональной связи η = 1. В отличие от коэффициента корреляции, корреляционное отношение не симметрично, то есть .

В условиях линейной зависимости между анализируемыми переменными, значение r и η совпадают. Поэтому величина разности между данными характеристиками может быть использована для обоснования правомерности описания изучаемой связи линейной регрессией.

Теоретическое корреляционное отношение, определяемое по результатам регрессионного анализа, рассчитывается путем деления факторной дисперсии, то есть дисперсии результативного признака, объяснённой вариацией признака-фактора, включённого в уравнение регрессии, на общую дисперсию признака-результата, обусловленную влиянием всех факторов:

или 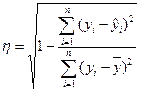(4.11)

где 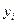- значение результативного признака у i-й единицы совокупности;

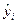- выровненное, то есть рассчитанное по уравнению регрессии, значение результативного признака у i-й единицы;

Квадрат корреляционного отношения (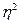) является коэффициентом детерминации и определяет долю вариации признака-результата, которая корреляционно связана с вариацией признака-фактора (факторов), т.е. характеризует долю объясненной дисперсии в общей дисперсии зависимой переменной. Корреляционное отношение и коэффициент детерминации являются универсальными измерителями степени тесноты связи.

Дата добавления: 2015-07-02